Теория и реализация языков программирования
[+]
Опубликован: 06.08.2007 | Доступ: свободный | Студентов: 1931 / 1080 | Оценка: 4.45 / 4.29 | Длительность: 18:50:00
Тема: Программирование
Специальности: Программист
Теги: beta, FPA, objective-c, YACC, автоматы, алгоритмы, анализ, внутренняя вершина, вычисления, дерево вывода, компиляторы, левая рекурсия, нетерминал, подцепочка, поиск, программирование, процедуры, регулярное множество, регулярные выражения, статическая цепочка, трансляторы, указатели, функция расстановки, элементы
Дополнительный материал 3:

Задачи по разделам курса
A
|
версия для печати
< Дополнительный материал 2 || Дополнительный материал 3: 12345678

Преобразования КС-грамматик

4.3.1. Указать множество бесполезных символов для грамматики:

S -> A|B; B -> aB|b|C; A -> AA|a; C -> cC:

4.3.2. Указать множество бесполезных символов в грамматике G = ({S, A, B, C}, {a, b, c}, P, S), где P состоит из

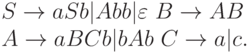
S \to aSb|Abb|\varepsilon\ B \to AB \\ A \to aBCb|bAb\ C \to a|c.

4.3.3. Указать множество бесполезных символов в грамматике G = ({S, A, B, C}, {a, b, c}, P, S), где P состоит из

S -> A|B 	A -> aB|bS|b
B -> AB|Ba 	C -> AS|b.

4.3.4. Указать множество бесполезных символов в грамматике G=({S, A, B, C, D}, {a, b, c}, P, S}, где P состоит из

S -> aBb|aCb 	A -> Dc|cA
B -> aS|b 	C -> AB|aD
D -> AB|cDa.

4.3.5. Указать множество бесполезных символов в грамматике G = ({S, A, B, C}, {0, 1, 2}, P, S), где P состоит из

S -> SS|A A -> 0A1|C|0
B -> 0C|1 C -> BC|CS.

4.3.6. Являются ли следующие грамматики приведeнными? Указать для каждой грамматики множества недостижимых, бесплодных и бесполезных символов:

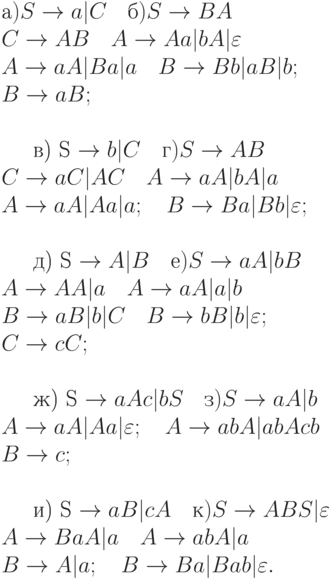
а) S \to a|C \ \ \ б) S \to BA \\ C \to AB \ \ \ A \to Aa|bA|\varepsilon \\ A \to aA|Ba|a \ \ \ B \to Bb|aB|b; \\ B \to aB; \\ \\ в) S \to b|C \ \ \ г) S \to AB \\ C \to aC|AC \ \ \ A \to aA|bA|a \\ A \to aA|Aa|a; \ \ \ B \to Ba|Bb|\varepsilon ; \\ \\ д) S \to A|B \ \ \ е) S \to aA|bB \\ A \to AA|a \ \ \ A \to aA|a|b \\ B \to aB|b|C \ \ \ B \to bB|b|\varepsilon ; \\ C \to cC; \\ \\ ж) S \to aAc|bS \ \ \ з) S \to aA|b \\ A \to aA|Aa|\varepsilon ; \ \ \ A \to abA|abAcb \\ B \to c; \\ \\ и) S \to aB|cA \ \ \ к) S \to ABS|\varepsilon \\ A \to BaA|a \ \ \ A \to abA|a \\ B \to A|a; \ \ \ B \to Ba|Bab|\varepsilon .

4.3.7. Построить приведeнные грамматики, эквивалентные следующим грамматикам:

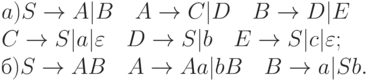
a) S \to A|B \ \ \ A \to C|D \ \ \ B \to D|E \\ C \to S|a|\varepsilon \ \ \ D \to S|b \ \ \ E \to S|c|\varepsilon ; \\ б) S \to AB \ \ \ A \to Aa|bB \ \ \ B \to a|Sb.

4.3.8. Построить \varepsilon -свободные КС-грамматики, эквивалентные следующим грамматикам:

1) S \to AB \ \ \ 2) S \to ABC \\ A \to C|ab \ \ \ A \to BB|\varepsilon \\ C \to c|\varepsilon \ \ \ B \to CC|\varepsilon \\ B \to aAa; \ \ \ C \to AA|b; \\ \\ 3) S \to aSbS \ \ \ 4) S \to AB \\ S \to bSaS|\varepsilon ; \ \ \ A \to SA|BB|bB \\ B \to b|aA|\varepsilon .

4.3.9. Доказать, что для каждой КС-грамматики существует эквивалентная ей приведенная КС-грамматика.

4.3.10. Привести алгоритм построения множества достижимых символов и доказать его правильность

4.3.11. Доказать, что для каждой КС-грамматики существует эквивалентная ей КС-грамматика, не являющаяся леворекурсивной

Дальше >>
< Дополнительный материал 2 || Дополнительный материал 3: 12345678

Вопросы и ответы

вопросов: 1
Анна Галкина
Анна Галкина
ответить