Языки и их представление
Алфавиты, цепочки и языки
Алфавит, или словарь - это конечное множество символов. Для обозначения символов мы будем пользоваться цифрами, латинскими буквами и специальными литерами типа 
Пусть V - алфавит. Цепочка в алфавите V - это любая строка конечной длины, составленная из символов алфавита V . Синонимом цепочки являются предложение, строка и слово. Пустая цепочка (обозначается e) - это цепочка, в которую не входит ни один символ.
Конкатенацией цепочек x и y называется цепочка xy. Заметим, что xe = ex = x для любой цепочки x.
Пусть x, y, z - произвольные цепочки в некотором алфавите. Цепочка y называется подцепочкой цепочки xyz. Цепочки x и y называются, соответственно, префиксом и суффиксом цепочки xy. Заметим, что любой префикс или суффикс цепочки является подцепочкой этой цепочки. Кроме того, пустая цепочка является префиксом, суффиксом и подцепочкой для любой цепочки.
Пример 2.1. Для цепочки abbba префиксом является любая цепочка из множества  суффиксом является любая цепочка из множества
суффиксом является любая цепочка из множества 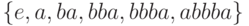 подцепочкой является любая цепочка из множества
подцепочкой является любая цепочка из множества 
Длиной цепочки w (обозначается |w| ) называется число символов в ней. Например, |abababa| = 7, а |e| = 0. Язык в алфавите V - это некоторое множество цепочек в алфавите V.
Пример 2.2. Пусть дан алфавит V = {a, b}. Вот некоторые языки в алфавите V:
-
 — пустой язык;
— пустой язык; -
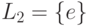 - язык, содержащий только пустую цепочку (заметим, что
- язык, содержащий только пустую цепочку (заметим, что 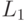 и
и 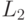 - различные языки)
- различные языки) -
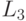 - язык, содержащий цепочки из a
и b, длина которых не превосходит 2
- язык, содержащий цепочки из a
и b, длина которых не превосходит 2 -
 - язык, включающий всевозможные цепочки из a и b, содержащие четное число a и четное число b
- язык, включающий всевозможные цепочки из a и b, содержащие четное число a и четное число b
-
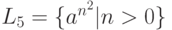 - язык цепочек из a, длины которых представляют собой квадраты натуральных чисел.
- язык цепочек из a, длины которых представляют собой квадраты натуральных чисел.
Два последних языка содержат бесконечное число цепочек.
Введем обозначение  для множества всех цепочек в
алфавите
для множества всех цепочек в
алфавите  , включая пустую цепочку. Каждый язык в
алфавите V является подмножеством
, включая пустую цепочку. Каждый язык в
алфавите V является подмножеством  . Для обозначения
множества всех цепочек в алфавите V , кроме пустой цепочки,
будем использовать
. Для обозначения
множества всех цепочек в алфавите V , кроме пустой цепочки,
будем использовать  .
.
Пример 2.3. Пусть 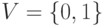 . Тогда
. Тогда 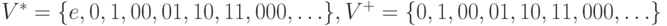
Введем некоторые операции над языками.
Пусть 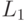 и
и 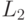 - языки в алфавите V. Конкатенацией
языков
- языки в алфавите V. Конкатенацией
языков 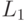 и
и 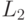 называется язык
называется язык 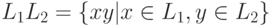 .
.
Пусть L - язык в алфавите V. Итерацией языка L
называется язык 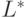 , определяемый следующим образом:
, определяемый следующим образом:
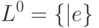 |
( 1) |
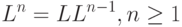 |
( 2) |
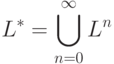 |
( 3) |
Пример 2.4. Пусть  и
и 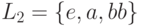 . Тогда
. Тогда
 , и
, и
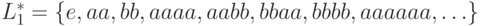
Большинство языков, представляющих интерес, содержат бесконечное число цепочек. При этом возникают три важных вопроса.
Во-первых, как представить язык (то есть специфицировать входящие в него цепочки)? Если язык содержит только конечное множество цепочек, ответ прост. Можно просто перечислить его цепочки. Если язык бесконечен, необходимо найти для него конечное представление. Это конечное представление, в свою очередь, будет строкой символов над некоторым алфавитом вместе с некоторой интерпретацией, связывающей это представление с языком.
Во-вторых, для любого ли языка существует конечное представление? Можно предположить, что ответ отрицателен. Мы увидим, что множество всех цепочек над алфавитом счетно. Язык - это любое подмножество цепочек. Из теории множеств известно, что множество всех подмножеств счетного множества несчетно. Хотя мы и не дали строгого определения того, что является конечным представлением, интуитивно ясно, что любое разумное определение конечного представления ведет только к счетному множеству конечных представлений, поскольку нужно иметь возможность записать такое конечное представление в виде строки символов конечной длины. Поэтому языков значительно больше, чем конечных представлений.
В-третьих, можно спросить, какова структура тех классов языков, для которых существует конечное представление?
Представление языков
Процедура - это конечная последовательность инструкций, которые могут быть механически выполнены. Примером может служить машинная программа. Процедура, которая всегда заканчивается, называется алгоритмом.
Один из способов представления языка - дать алгоритм, определяющий, принадлежит ли цепочка языку. Более общий способ состоит в том, чтобы дать процедуру, которая останавливается с ответом "да" для цепочек, принадлежащих языку, и либо останавливается с ответом "нет", либо вообще не останавливается для цепочек, не принадлежащих языку. Говорят, что такая процедура или алгоритм распознает язык.
Такой метод представляет язык с точки зрения распознавания. Язык можно также представить методом порождения. А именно, можно дать процедуру, которая систематически порождает в определенном порядке цепочки языка.
Если мы можем распознать цепочки языка над алфавитом V либо с помощью процедуры, либо с помощью алгоритма,
то мы можем и генерировать язык, поскольку мы можем
систематически генерировать все цепочки из  , проверять
каждую цепочку на принадлежность языку и выдавать
список только цепочек языка. Но если процедура не
всегда заканчивается при проверке цепочки, мы не
сдвинемся дальше первой цепочки, на которой процедура
не заканчивается. Эту проблему можно обойти, организовав
проверку таким образом, чтобы процедура никогда не
продолжала проверять одну цепочку бесконечно. Для этого
введем следующую конструкцию.
, проверять
каждую цепочку на принадлежность языку и выдавать
список только цепочек языка. Но если процедура не
всегда заканчивается при проверке цепочки, мы не
сдвинемся дальше первой цепочки, на которой процедура
не заканчивается. Эту проблему можно обойти, организовав
проверку таким образом, чтобы процедура никогда не
продолжала проверять одну цепочку бесконечно. Для этого
введем следующую конструкцию.
Предположим, что V имеет p символов. Мы можем
рассматривать цепочки из  как числа, представленные
в базисе p, плюс пустая цепочка e. Можно занумеровать
цепочки в порядке возрастания длины и в "числовом"
порядке для цепочек одинаковой длины. Такая нумерация
для цепочек языка
как числа, представленные
в базисе p, плюс пустая цепочка e. Можно занумеровать
цепочки в порядке возрастания длины и в "числовом"
порядке для цепочек одинаковой длины. Такая нумерация
для цепочек языка 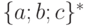 приведена на
рис.
2.1, а.
приведена на
рис.
2.1, а.
Пусть P - процедура для проверки принадлежности цепочки языку L. Предположим, что P может быть представлена дискретными шагами, так что имеет смысл говорить об i -ом шаге процедуры для любой данной цепочки. Прежде чем дать процедуру перечисления цепочек языка L, дадим процедуру нумерации пар положительных чисел.
Все упорядоченные пары положительных чисел (x, y) можно отобразить на множество положительных чисел следующей формулой:
z = (x + y - 1)(x + y - 2)/2 + y
Пары целых положительных чисел можно упорядочить в соответствии со значением z ( рис. 2.1, б).
