Теория и реализация языков программирования
[+]
Дополнительный материал 3:

Задачи по разделам курса
A
|
версия для печати
< Дополнительный материал 2 || Дополнительный материал 3: 12345678

Синтаксический анализ

КС-грамматики и МП-автоматы

4.1.1. Пусть G - грамматика с правилами:

S -> SbS|ScS|a

Найти 2 различных дерева вывода для цепочки abaca.

4.1.2. Дана однозначная КС-грамматика G = (N, T, P, S) и цепочка w \in L(G). Количество элементов во множествах N, T, P равно n1, n2, n3 соответственно, а |w| = l. Найти нижнюю и верхнюю границу для числа деревьев разбора w в G.

4.1.3. Являются ли однозначными следующие грамматики?

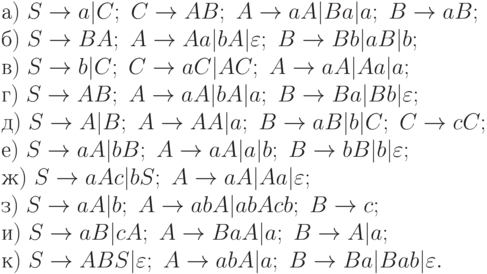
а)\ S \to a|C;\ C \to AB;\ A \to aA|Ba|a;\ B \to aB; \\ б)\ S \to BA;\ A \to Aa|bA|\varepsilon ;\ B \to Bb|aB|b; \\ в)\ S \to b|C;\ C \to aC|AC;\ A \to aA|Aa|a; \\ г)\ S \to AB;\ A \to aA|bA|a;\ B \to Ba|Bb|\varepsilon ; \\ д)\ S \to A|B;\ A \to AA|a;\ B \to aB|b|C;\ C \to cC; \\ е)\ S \to aA|bB;\ A \to aA|a|b;\ B \to bB|b|\varepsilon ; \\ ж)\ S \to aAc|bS;\ A \to aA|Aa|\varepsilon ; \\ з)\ S \to aA|b;\ A \to abA|abAcb;\ B \to c; \\ и)\ S \to aB|cA;\ A \to BaA|a;\ B \to A|a; \\ к)\ S \to ABS|\varepsilon ;\ A \to abA|a;\ B \to Ba|Bab|\varepsilon .

4.1.4. Является ли однозначной грамматика с правилами:

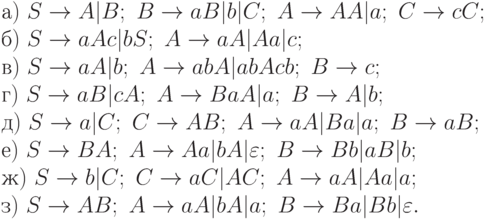
а)\ S \to A|B;\ B \to aB|b|C;\ A \to AA|a;\ C \to cC; \\ б)\ S \to aAc|bS;\ A \to aA|Aa|c; \\ в)\ S \to aA|b;\ A \to abA|abAcb;\ B \to c; \\ г)\ S \to aB|cA;\ A \to BaA|a;\ B \to A|b; \\ д)\ S \to a|C;\ C \to AB;\ A \to aA|Ba|a;\ B \to aB; \\ е)\ S \to BA;\ A \to Aa|bA|\varepsilon ;\ B \to Bb|aB|b; \\ ж)\ S \to b|C;\ C \to aC|AC;\ A \to aA|Aa|a; \\ з)\ S \to AB;\ A \to aA|bA|a;\ B \to Ba|Bb|\varepsilon .

4.1.5. Пусть G1 - грамматика, имеющая продукции:

S -> bA|ab; A -> a|aS|bAA; B -> b|bS|aBB;

а G2 - грамматика, определяемая продукциями:

S -> aB|aBS|bAS|bA; A -> bAA|a; B -> bBB|b.

Показать, что

1) G1 - неоднозначная грамматика;
2) G2 - однозначная грамматика;
3) L(G1) = L(G2):

4.1.6. Какой язык допускается автоматом с магазинной памятью

P = (Хq_{0}\} , \{ a, b\} , \{ z_{0}\} , \varnothing , q_{0}, z_{0}, \{ q_{0}\} ) ?

4.1.7. Построить МП-автоматы, определяющие языки

а)\ \{ ww^{R} : w \in \{ a, b\} ^{*}\} ; \\ б)\ язык\ всех\ цепочек\ из\ нулей\ и\ единиц\ с\ одинаковым\ числом \\ тех\ и\ других \\ в)\ \{ \{ a, b\} ^{*} \setminus \{ a^{m}b^{n}a^{m}b^{n}\} : m, n \ge 1\} ; \\ г)\ \{ \{ a, b\} ^{*} \setminus \{ a^{m}b^{n}a^{m}\} : m, n \ge 1\} ; \\ д)\ \{ \{ a, b\} ^{*} \setminus \{ ww\} : w \in \{ a, b]^{*}\} :

4.1.8. Построить автомат с магазинной памятью, допускающий язык:

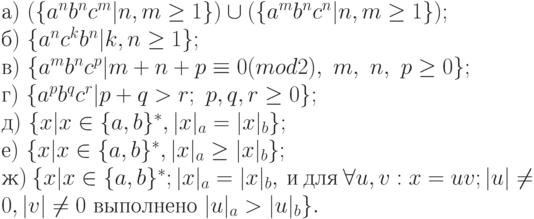
а)\ (\{ a^{n}b^{n}c^{m}|n, m \ge 1\} ) \cup (\{ a^{m}b^{n}c^{n}|n, m \ge 1\} ); \\ б)\ \{ a^{n}c^{k}b^{n}|k, n \ge 1\} ; \\ в)\ \{ a^{m}b^{n}c^{p}|m + n + p \equiv 0(mod2),\ m,\ n,\ p \ge 0\} ; \\ г)\ \{ a^{p}b^{q}c^{r}|p + q > r;\ p, q, r \ge 0\} ; \\ д)\ \{ x|x \in \{ a, b\} ^{*}, |x|_{a} = |x|_{b}\} ; \\ е)\ \{ x|x \in \{ a, b\} ^{*}, |x|_{a} \ge |x|_{b}\} ; \\ ж)\ \{ x|x \in \{ a, b\} ^{*}; |x|_{a} = |x|_{b},\ и\ для\ \forall u, v : x = uv; |u| \ne 0, |v| \ne 0\ выполнено\ |u|_{a} > |u|_{b}\} .

4.1.9. Пусть A - магазинный автомат. Построить магазинный автомат B, допускающий все префиксы языка

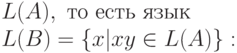
L(A),\ то\ есть\ язык\\ L(B) = \{ x|xy \in L(A)\} :

4.1.10. Построить детерминированные МП-автоматы, определяющие языки:

а)\ \{ wcw^{R} : w \in \{ a, b\} ^{*}\} ; \\ б)\ \{ 0^{n}1^{n} : n \ge 1\} \\ в)\ \{ xcx^{R}ycy^{R}|x, y \in \{ a, b\} ^{*}\} .

4.1.11. Является ли язык L = \{ xcx^{R}|x \in (a*b*)*\} детерминированным? Обосновать ответ с помощью магазинного автомата, допускающего язык L.

4.1.12. Является ли детерминированным следующий язык:

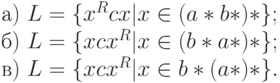
а)\ L = \{ x^{R}cx|x \in (a*b*)*\} ; \\ б)\ L = \{ xcx^{R}|x \in (b*a*)*\} ; \\ в)\ L = \{ xcx^{R}|x \in b*(a*)*\} .

4.1.13. Доказать, что для любой КС-грамматики G' существует эквивалентная ей КС грамматика G, имеющая лишь правила вида

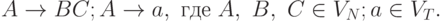
A \to BC; A \to a ,\ где\ A,\ B,\ C \in V_{N}; a \in V_{T} .

4.1.14. Доказать, что если L1 - КС-язык, то язык L, состоящий из всех слов L1 четной длины - КС-язык, то есть

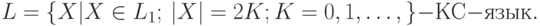
L = \{ X|X \in L_{1};\ |X| = 2K; K = 0, 1, \dots , \} - КС-язык.

4.1.15. Доказать, что для КС-грамматики G существует неукорачивающая КС-грамматика G', порождающая язык

L(G') = L(G) \setminus \{ \varepsilon \} .

4.1.16. Привести алгоритм, позволяющий узнать, принадлежит ли данное слово данному КС-языку и доказать его правильность.

4.1.17. КС-грамматика называется левооднозначной, если каждое слово порождаемого ею языка имеет единственный левый вывод. Аналогично определяется правооднозначная грамматика. Построить пример левооднозначной, но не правооднозначной КС-грамматики.

C.4.2. Алгебраические свойства КС-языков. Лемма о разрастании.

4.2.1. Пусть L1, L2 - КС-языки. Докажите:

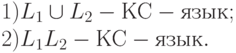
1) L_{1} \cup L_{2} - КС-язык; \\ 2) L_{1}L_{2} - КС-язык.

4.2.2. Пусть L - КС-язык. Докажите:

1) L* - КС-язык;
2) LR - КС-язык.

4.2.3. Доказать, что не существует КС-грамматик, порождающих языки

а) {anbncn} : n >= 1}; б) \{ ww : w \in \{ a, b\} ^{*}\} ;

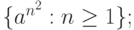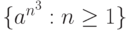в) \{ a^{n^2} : n \geq 1 \}; г) \{a^{n^3} : n \geq 1\}.

4.2.4. Выяснить, какие из приведенных ниже языков не являются КС-языками:

1)\ \{ a^{i}b^{j}c^{k}|0 \le i <j< k\} ; \\ 2)\ \{ a^{i}b^{j}c^{k}|0 \le i =j= k\} ; \\ 3)\ \{ a^{i}b^{j}c^{k}|0 \le i = j, k \ge 0,\ i \ne k\} ; \\ 4)\ \{ a^{i}b^{j}c^{k}|0 \le i = j,\ k \ge 0\} :

4.2.5. Показать, что язык {anbncn|n>=1g не является КС-языком.

4.2.6. Является ли язык {anbmanbm|n >= 1, m >= 1 } КС-языком?

4.2.7. Является ли язык {anbmbnam|n >= 1, m >= 1} КС-языком?

4.2.8. Является ли язык {ap|p - простое число} КС- языком?

4.2.9. Является ли язык \{a^nb^{n^2} \mid n \in N \} КС-языком?

4.2.10. Определить, замкнуто ли множество КС-языков относительно дополнения?

4.2.11. Замкнуто ли множество КС-языков относительно обращения? (Иначе говоря, верно ли, что если L - КС-язык, то LR - тоже КС-язык).

Дальше >>
< Дополнительный материал 2 || Дополнительный материал 3: 12345678

Вопросы и ответы

вопросов: 1
Анна Галкина
Анна Галкина
ответить