Синтаксический анализ
Теорема 4.3. Пусть  - расширенный МП-автомат. Тогда существует МП-
автомат M' , такой, что L(M') = L(M).
- расширенный МП-автомат. Тогда существует МП-
автомат M' , такой, что L(M') = L(M).
Расширенный МП-автомат 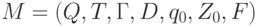 называется детерминированным, если выполнены следующие
условия:
называется детерминированным, если выполнены следующие
условия:
(1) Множество D(q, a, u) содержит не более одного элемента
для любых  ,
,
(2) Если  и
и  , то не существует цепочки x такой, что u = vx или v = ux,
, то не существует цепочки x такой, что u = vx или v = ux,
(3) Если  , то не существует
цепочки x такой, что u = vx или v = ux.
, то не существует
цепочки x такой, что u = vx или v = ux.
Теорема 4.4. Пусть 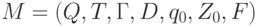 - расширенный ДМП-автомат. Тогда существует ДМП- автомат M' , такой, что L(M') = L(M).
- расширенный ДМП-автомат. Тогда существует ДМП- автомат M' , такой, что L(M') = L(M).
ДМП-автомат и расширенный ДМП-автомат лежат в основе рассматриваемых далее в этой главе, соответственно, LL- и LR-анализаторов.
Определение. Говорят, что КС-грамматика находится в нормальной форме Хомского, если каждое правило имеет вид:
(1) либо A -> BC, A, B, C - нетерминалы,
(2) либо A -> a, a - терминал,
(3) либо S -> e и в этом случае S - не встречается в правых частях правил.
Утверждение. Любую КС-грамматику можно преобразовать в эквивалентную ей в нормальной форме Хомского.
Утверждение. Если КС-грамматика находится в
нормальной форме Хомского, тогда для любой цепочки 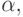 если
если 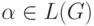 и m - высота дерева вывода с кроной
и m - высота дерева вывода с кроной  .
.
Теорема 4.5. (Лемма о разрастании для контекстно-
свободных языков). Для любого КС-языка L существуют
такие целые l и k, что любая цепочка 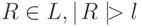 , представима в виде R = uvwxy, где
, представима в виде R = uvwxy, где
(1) |vwx| <= k
(2) 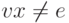
(3)  для любого i >= 0.
для любого i >= 0.
Доказательство.
Пусть L = L(G), где  - контекстно-
свободная грамматика в нормальной форме Хомского.
Обозначим через n число нетерминалов, т.е. n = |N|, и
рассмотрим l = 2n и k = 2n+1.
- контекстно-
свободная грамматика в нормальной форме Хомского.
Обозначим через n число нетерминалов, т.е. n = |N|, и
рассмотрим l = 2n и k = 2n+1.
Для доказательства того, что l и k удовлетворяют условию
теоремы, рассмотрим произвольную цепочку 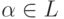 , для
которой
, для
которой 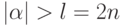 . В силу Утверждения получаем, что
высота дерева с кроной
. В силу Утверждения получаем, что
высота дерева с кроной  больше n + 1 и есть путь по дереву
(обозначим его через P ), который проходит более чем через n + 1 вершин. Отсюда по определению дерева вывода имеем,
что P содержит более n вершин, помеченных нетерминалами.
Таким образом, существует нетерминал, который метит не
менее двух вершин пути P. Среди всех таких нетерминалов
пусть A - такой, что его вхождение, ближайшее к листу, не
содержит других нетерминалов, обладающих этим свойством
(если бы это было не так, то выбрали бы этот другой). Пусть q
- вхождение A, ближайшее к листу, p - расположенное выше.
Представим крону
больше n + 1 и есть путь по дереву
(обозначим его через P ), который проходит более чем через n + 1 вершин. Отсюда по определению дерева вывода имеем,
что P содержит более n вершин, помеченных нетерминалами.
Таким образом, существует нетерминал, который метит не
менее двух вершин пути P. Среди всех таких нетерминалов
пусть A - такой, что его вхождение, ближайшее к листу, не
содержит других нетерминалов, обладающих этим свойством
(если бы это было не так, то выбрали бы этот другой). Пусть q
- вхождение A, ближайшее к листу, p - расположенное выше.
Представим крону  в виде uvwxy, где w - крона поддерева D1 с корнем q и vwx - крона поддерева D2 с корнем p. Тогда
высота поддерева D2 не более (n - 1) + 2 + 1 = n + 2, так что |vwz| <= 2n+1.
в виде uvwxy, где w - крона поддерева D1 с корнем q и vwx - крона поддерева D2 с корнем p. Тогда
высота поддерева D2 не более (n - 1) + 2 + 1 = n + 2, так что |vwz| <= 2n+1.
Также очевидно, что 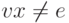 , поскольку в силу определения
нормальной формы Хомского p имеет двух сыновей,
помеченных нетерминалами, из которых не выводится пустая
цепочка.
, поскольку в силу определения
нормальной формы Хомского p имеет двух сыновей,
помеченных нетерминалами, из которых не выводится пустая
цепочка.
Кроме того, S =>* u Ay =>* uvAxy =>* uvwxy, а также A =>* vAx =>* vwx. Отсюда получаем A =>* viwxi для всех i >= 0 и S =>* uviwxiy для всех i >= 0.
Пример. Покажем, что язык L = {anbncn|n>=1} не является контекстно-свободным языком.
Если бы он был КС-языком, то мы взяли бы константу k,
которая определяется в лемме о разрастании. Пусть z = akbkck.
Тогда z = uvwxy. Так как |vwx| <= k, то в цепочке vwx не могут
быть вхождения каждого из символов a, b и c. Таким образом,
цепочка uwy, которая по лемме о разрастании принадлежит L,
содержит либо k символов a, либо k символов c. Но она не может
иметь k вхождений каждого из символов a, b и c, потому, что |uwy| < 3k. Значит, вхождений какого-то из этих символов в
uwy больше, чем другого и, следовательно,  . Полученное
противоречие позволяет заключить, что L - не КС-язык.
. Полученное
противоречие позволяет заключить, что L - не КС-язык.
