НОУ ИНТУИТ | Теория и реализация языков программирования. Лекция 5: Синтаксический анализ

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 06.08.2007 | Доступ: свободный | Студентов: 1930 / 1080 | Оценка: 4.45 / 4.29 | Длительность: 18:50:00

Тема: Программирование

Специальности: Программист

|

Вам нравится? Нравится 18 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

LL(k)-грамматики

Определение. КС-грамматика $G = (N, \Sigma , P, S)$ называется LL(k)-грамматикой для некоторого фиксированного k, если из

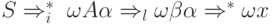
(1) $S \Rightarrow^*_i \; \omega A \alpha \Rightarrow_l \omega \beta \alpha \Rightarrow^* \omega x$

(2) $S \Rightarrow^*_i \; \omega A \alpha \Rightarrow_l \omega \gamma \alpha \Rightarrow^* \omega x$ для которых

и

FIRST_k(x) = FIRST_k(y), вытекает, что $\beta = \gamma$ .

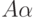Говоря менее формально, G будет LL(k)- грамматикой, если для данной цепочки $\omega A \alpha \in (N \cup \Sigma)^*$ и первых k символов (если они есть), выводящихся из $A\alpha$ , существует не более одного правила, которое можно применить к A, чтобы получить вывод какой-нибудь терминальной цепочки,

Рис. 4.4.

начинающейся с $\omega$ и продолжающейся упомянутыми k терминалами.

Грамматика называется LL(k)-грамматикой, если она LL(k)-грамматика для некоторого k.

Пример 4.7. Рассмотрим грамматику G = ({S, A, B}, {0, 1, a, b}, P, S), где P состоит из правил

S -> A | B,
	A -> aAb | 0,
	B -> aBbb | 1.

Здесь $L(G) = a^{n}0b^{n} | n \ge 0 \cup a^{n}1b^{2n} | n \ge 0$ . G не является LL(k)-грамматикой ни для какого k. Интуитивно, если мы начинаем с чтения достаточно длинной цепочки, состоящей из символов a, то не знаем, какое из правил S -> A и S -> B было применено первым, пока не встретим 0 или 1.

Обращаясь к точному определению LL(k)-грамматики, положим $\omega = \alpha = e; \beta = A; \gamma = B; x = a^{k}0b^{k}$ и y = a^k1b^2k. Тогда выводы

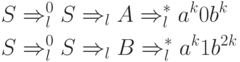
$\begin{align*} &S \Rightarrow^0_l S \Rightarrow_l A \Rightarrow^*_l a^k0b^k \\ &S \Rightarrow^0_l S \Rightarrow_l B \Rightarrow^*_l a^k1b^{2k} \end{align*}$

соответствуют выводам (1) и (2) определения. Первые k символов цепочек x и y совпадают. Однако заключение $\beta = \gamma$ ложно. Так как k здесь выбрано произвольно, то G не является LL-грамматикой.

Следствия определения LL(k)- грамматики

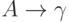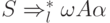Теорема 4.6. КС-грамматика $G = (N, \Sigma , P, S)$ является LL(k)-грамматикой тогда и только тогда, когда для двух различных правил $A \to \beta$ и $A \to \gamma$ из Р пересечение $FIRST_{k}(\beta \alpha ) \cap FIRST_{k}(\gamma \alpha )$ пусто при всех таких $\omega A\alpha$ , что $S \Rightarrow^*_l \omega A \alpha$ .

Доказательство. Необходимость. Допустим, что $\omega , A, \alpha , \beta$ и $\gamma$ удовлетворяют условиям теоремы, а $FIRST_{k}(\beta \alpha ) \cap FIRST_{k}(\gamma \alpha )$ содержит x. Тогда по определению FIRST для некоторых y и z найдутся выводы

$\begin{align*} &S \Rightarrow^*_l \omega A \alpha \Rightarrow_l \omega \beta \alpha \Rightarrow^*_l \omega x y \\ & \text{и}\\ &S \Rightarrow^*_l \omega A \alpha \Rightarrow_l \omega \gamma \alpha \Rightarrow^*_l \omega x y \end{align*}$

(Заметим, что здесь мы использовали тот факт, что N не содержит бесполезных нетерминалов, как это предполагается для всех рассматриваемых грамматик.) Если |x| < k ; то y = z = e. Так как 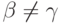$\beta \ne \gamma$ , то G не LL(k)-грамматика.

Достаточность. Допустим, что G не LL(k)-грамматика.

Тогда найдутся такие два вывода

$\begin{align*} &S \Rightarrow^*_l \omega A \alpha \Rightarrow_l \omega \beta \alpha \Rightarrow^*_l \omega x \\ & \text{и}\\ &S \Rightarrow^*_l \omega A \alpha \Rightarrow_l \omega \gamma \alpha \Rightarrow^*_l \omega y \end{align*}$

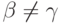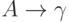что цепочки x и y совпадают в первых k позициях, но $\beta \ne \gamma$ . Поэтому $A \to \beta$ и $A \to \gamma$ - различные правила из P и каждое из множеств $FIRSTk(\beta \alpha )$ и $FIRSTk(\gamma \alpha )$ содержит цепочку FIRST_k(x), совпадающую с цепочкой FIRST_k(y).

Пример 4.8. Грамматика G, состоящая из двух правил S -> aS | a, не будет LL(1)-грамматикой, так как

FIRST₁(aS) = FIRST₁(a) = a.

Интуитивно это можно объяснить так: видя при разборе цепочки, начинающейся символом a, только этот первый символ, мы не знаем, какое из правил S -> aS или S -> a надо применить к S. С другой стороны, G - это LL(2)-грамматика. В самом деле, в обозначениях только что представленной теоремы, если 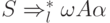$S \Rightarrow^*_l \omega A \alpha$ , то A = S и $\alpha = e$ . Так как для S даны только два указанных правила, то $\beta = aS$ и $\gamma = a$ . Поскольку FIRST2(aS) = aa и FIRST2(a) = a, то по последней теореме G будет LL(2)-грамматикой.

Удаление левой рекурсии

Основная трудность при использовании предсказывающего анализа - это нахождение такой грамматики для входного языка, по которой можно построить таблицу анализа с однозначно определенными входами. Иногда с помощью некоторых простых преобразований грамматику, не являющуюся LL(1), можно привести к эквивалентной LL(1)-грамматике. Среди этих преобразований наиболее эффективными являются левая факторизация и удаление левой рекурсии. Здесь необходимо сделать два замечания. Во-первых, не всякая грамматика после этих преобразований становится LL(1), и, во-вторых, после таких преобразований получающаяся грамматика может стать менее понимаемой.

Непосредственную левую рекурсию, то есть рекурсию вида $A\to A\alpha$ , можно удалить следующим способом. Сначала группируем A -правила:

$A \to A\alpha _{1} |A\alpha _{2}| \dots |A\alpha _{m}|\beta _{1}|\beta _{2}| \dots |\beta _{n};$

где никакая из строк 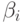$\beta _{i}$ не начинается с A. Затем заменяем этот набор правил на

$\begin{align*} &A\rightarrow\beta_1A' \mid \beta_2A' \mid \ldots \mid \beta_nA'\\ &A'\rightarrow\alpha_1A' \mid \alpha_2A' \mid \ldots \mid \alpha_nA'\mid e\\ \end{align*}$

где A' - новый нетерминал. Из нетерминала A можно вывести те же цепочки, что и раньше, но теперь нет левой рекурсии. С помощью этой процедуры удаляются все непосредственные левые рекурсии, но не удаляется левая рекурсия, включающая два или более шага. Приведенный ниже алгоритм 4.8 позволяет удалить все левые рекурсии из грамматики.

Алгоритм 4.8. Удаление левой рекурсии.

Вход. КС-грамматика G без e-правил (вида A -> e ).

Выход. КС-грамматика G' без левой рекурсии, эквивалентная G.

Метод. Выполнить шаги 1 и 2.

(1) Упорядочить нетерминалы грамматики G в произвольном порядке.

(2) Выполнить следующую процедуру:

$\begin{align*} \textbf{fo}&\textbf{r} (i=1;i<=n;i++)\{\\ &\textbf{for} (j=1;j<=i-1;j++) \{ \\ &\quad \text{пусть } A_j \rightarrow \beta_1\mid \beta_2 \mid \ldots \mid \beta_k \text{ - все текущие правила }\\ &\quad\text{для } A_j;\\ &\quad\text{заменить все правила вида } A_i \rightarrow A_j \alpha\\ &\quad \text{на правила } A_i \rightarrow \beta_1\alpha \mid \beta_2 \alpha \mid \ldots \mid \beta_k \alpha ;\\ &\;\}\\ &\; \text{удалить правила вида } A_i \rightarrow A_i; \\ &\; \text{удалить непосредственную левую рекурсию в} \\ &\; \text{правилах для } A_i;\\ \} \end{align*}$

После (i-1) -й итерации внешнего цикла на шаге 2 для любого правила вида $A_{k} \to A_{s}\alpha$ , где k < i, выполняется s > k. В результате на следующей итерации (по i ) внутренний цикл (по j ) последовательно увеличивает нижнюю границу по m в любом правиле $A_{i} \to A_{m}\alpha$ , пока не будет m >= i. Затем, после удаления непосредственной левой рекурсии для A_i -правил, m становится больше i.

Алгоритм 4.8 применим, если грамматика не имеет e - правил (правил вида A -> e ). Имеющиеся в грамматике e - правила могут быть удалены предварительно. Получающаяся грамматика без левой рекурсии может иметь e -правила.

Левая факторизация

Oсновная идея левой факторизации в том, что в том случае, когда неясно, какую из двух альтернатив надо использовать для развертки нетерминала A, нужно изменить A -правила так, чтобы отложить решение до тех пор, пока не будет достаточно информации для принятия правильного решения.

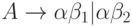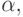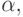Если $A \to \alpha \beta _{1} | \alpha \beta _{2}$ - два A -правила и входная цепочка начинается с непустой строки, выводимой из $\alpha,$ мы не знаем, разворачивать ли по первому правилу или по второму. Можно отложить решение, развернув $A \to \alpha A'$ . Тогда после анализа того, что выводимо из $\alpha,$ можно развернуть по $A' \to \beta _{1}$ или по $A' \to \beta _{2}$ . Левофакторизованные правила принимают вид

$A\to \alpha A'$

$A'\to \beta _{1}|\beta _{2}$

Алгоритм 4.9. Левая факторизация грамматики.

Вход. КС-грамматика G.

Выход. Левофакторизованная КС-грамматика G', эквивалентная G.

Метод. Для каждого нетерминала A найти самый длинный префикс 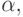$\alpha,$ общий для двух или более его альтернатив. Если $\alpha \ne e$ , то есть существует нетривиальный общий префикс, заменить все A -правила

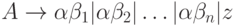$A \to \alpha \beta _{1}|\alpha \beta _{2}| \dots |\alpha \beta _{n}|z$ ,

где z обозначает все альтернативы, не начинающиеся с 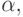$\alpha,$ на

$A \to \alpha A'|z$

$A'\to \beta _{1}|\beta _{2}| \dots |\beta _{n}$

где A' - новый нетерминал. Применять это преобразование, пока никакие две альтернативы не будут иметь общего префикса.

Пример 4.9. Рассмотрим вновь грамматику условных операторов из примера 4.6:

S -> if E then S | if E then S else S | a
  E -> b

После левой факторизации грамматика принимает вид

S -> if E then SS' | a
  S' -> else S | e
  E -> b

К сожалению, грамматика остается неоднозначной, а значит, и не LL(1)-грамматикой.

Дальше >>

Авторизоваться

Теория и реализация языков программирования

Синтаксический анализ

LL(k)-грамматики

Следствия определения LL(k)- грамматики

Удаление левой рекурсии

Левая факторизация

Вопросы и ответы