Синтаксический анализ

Преобразования КС-грамматик

Рассмотрим ряд преобразований, позволяющих "улучшить" вид контекстно-свободной грамматики без изменения порождаемого ею языка.

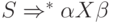Назовем символ недостижимым в КС- грамматике G = (N, T, P, S), если X не появляется ни в одной выводимой цепочке этой грамматики. Иными словами, символ X является недостижимым, если в G не существует вывода ни для каких .

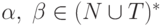Назовем символ несводимым (бесплодным) в той же грамматике, если в ней не существует вывода вида X =>^* xwy, где w, x, y принадлежат T^*.

Очевидно, что каждый недостижимый и/или несводимый символ является бесполезным, как и все правила, его содержащие.

При внимательном изучении вышеприведенных определений становится понятным, что а) целесообразно искать не непосредственно сами недостижимые (или несводимые) символы, а последовательно определять множество достижимых (или сводимых) символов, начиная с тех, которые по определению являются достижимыми (аксиома) и сводимыми (терминалы) - все остальные символы оказываются бесполезными, б) одновременное определение достижимых и сводимых символов невозможно, так как соответствующие процессы идут в противоположных направлениях (от корня к листьям и наоборот).

Алгоритм 4.1. Устранение недостижимых символов.

Вход. КС-грамматика G = (N, T, P, S).

Выход. КС-грамматика G' = (N', T', P', S) без недостижимых символов, такая, что L(G') = L(G).

Метод. Выполнить шаги 1-4:

(1) Положить V₀ = {S} и i = 1,

(2) Положить V_i = {X | в P есть 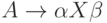и ,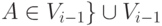

(3) Если , положить i = i + 1 и перейти к шагу 2, в противном случае перейти к шагу 4,

(4) Положить . Включить в P' все правила из P, содержащие только символы из V_i.

Алгоритм 4.2. Устранение несводимых символов.

Вход. КС-грамматика G = (N, T, P, S).

Выход. КС-грамматика G' = (N', T', P', S) без несводимых символов, такая, что L(G') = L(G).

Метод. Выполнить шаги 1-4:

(1) Положить N' = T и i = 1,

(2) Положить ,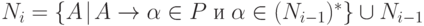

(3) Если 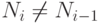, положить i = i + 1 и перейти к шагу 2, в противном случае положить N_e = N_i и перейти к шагу 4,

(4) Положить 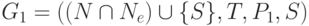, где P₁ состоит из правил множества P, содержащих только символы из ,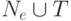

Чтобы устранить все бесполезные символы, необходимо применить к исходной грамматике сначала Алгоритм 4.2, а затем Алгоритм 4.1.

Пример. Все символы следующей грамматики

S -> AS | b

A -> AB

B -> a

являются достижимыми. Поэтому нарушение предложенного порядка применения к ней алгоритмов приведет лишь к частичному решению задачи.

КС-грамматика без бесполезных символов называется приведенной. Легко видеть, что для любой КС-грамматики существует эквивалентная приведенная. В дальнейшем будем предполагать, что все рассматривамые грамматики - приведенные.

Алгоритм Кока-Янгера-Касами

Приведем алгоритм синтаксического анализа, применимый для любой грамматики в нормальной форме Хомского

Алгоритм Кока-Янгера-Касами

Вход. КС-грамматика G = (N, T, P, S) в нормальной форме Хомского и входная цепочка .

Выход. Таблица разбора Tab для w такая, что 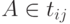тогда и только тогда, когда A =>⁺ a_ia_i+1 ... a_i+j-1.

Метод.

(1) Положить 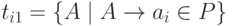для каждого i. Так что, если 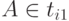, то A =>⁺ a_i.

(2) Пусть t_ij вычислено для 1<=i<=n и 1<= j' < j. Положим t_ij = {A| для некоторого 1 <= k < j правило .

Так как 1 <= k < j, то k < j и j - k < j. Так что t_ik и t_i+k,j-k вычисляются раньше, чем t_ij. Если то A => BC =>⁺ a_i a_i+k-1 C =>⁺ a_I ... a_i+k-1a_i+k ... a_i+j-1.

(3) Повторять шаг 2 до тех пор, пока не станут известны t_ij для всех 1 <= i <= n и 1 <= j <= n-i+1.

Алгоритм нахождения левого разбора по таблице разбора Tab.

Вход. КС-грамматика G = (N, T, P, S) в нормальной форме Хомского с правилами, занумерованными от 1 до p, входная цепочка и таблица разбора Tab.

Выход. Левый разбор цепочки w или сигнал ошибка.

Метод. Процедура gen(i, j, A):

(1) Если j = 1 и A => a_i = p_m, выдать m.

(2) Пусть j > 1 и k - наименьшее из чисел от 1 до j-1, для которых существует и правило pm = A -> BC. Выдать m и выполнить gen(i, k, B), затем gen(i + k, j - k, C).

Выполнить gen(1, n, S), если 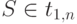, иначе ошибка.