Квантовые вероятности
Задача 9.1. Докажите, что операторы вида 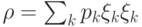 — это в точности эрмитовы неотрицательно определенные операторы со следом 1, т.е. операторы, удовлетворяющие условиям:
— это в точности эрмитовы неотрицательно определенные операторы со следом 1, т.е. операторы, удовлетворяющие условиям:
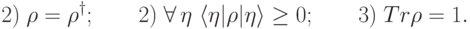
В дальнейшем под матрицей плотности понимается любой оператор с этими свойствами.
Рассуждение о "распределении вероятностей на квантовых состояниях" носило вспомогательный характер. Задача состоит в том, чтобы обобщить понятие квантового состояния так, чтобы оно включало в себя классические распределения вероятностей. Полученный нами ответ (последнее выражение в (9.2)) зависит лишь от матрицы плотности, поэтому мы можем постулировать, что обобщенные квантовые состояния и матрицы плотности — это одно и то же (такая аксиома не противоречит физическим наблюдениям). Если состояние задается одним вектором ( 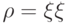 ), то оно называется чистым, если состояние задается общей матрицей плотности, то оно называется смешанным.
), то оно называется чистым, если состояние задается общей матрицей плотности, то оно называется смешанным.
Определение 9.1. Для квантового состояния, задаваемого матрицей плотности  , и подпространства
, и подпространства  вероятность "события"
вероятность "события"  равна
равна 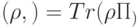 .
.
Диагональные матрицы 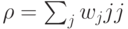 соответствуют классическим распределениям вероятностей на множестве базисных векторов. Это означает, что при вычислении вероятности по общей квантовой формуле для диагональной матрицы и координатного подпространства
соответствуют классическим распределениям вероятностей на множестве базисных векторов. Это означает, что при вычислении вероятности по общей квантовой формуле для диагональной матрицы и координатного подпространства  (натянутого на часть базисных векторов
(натянутого на часть базисных векторов 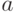 :
: 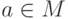 ) получается то же, что и при вычислении по обычной классической формуле:
) получается то же, что и при вычислении по обычной классической формуле: 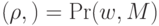 .
.
Продолжим сравнение свойств классической и квантовой вероятности, под последней мы будем теперь понимать общее определение с использованием матриц плотности. (Свойства 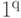 и
и 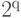 остаются в силе).
остаются в силе).
Определение 9.2. Пусть 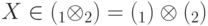 . Частичный след оператора
. Частичный след оператора  по пространству
по пространству 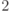 определен следующим образом: если
определен следующим образом: если 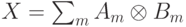 , то
, то 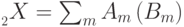 .
.
Докажем, что это определение корректно, т.е. не зависит от выбора слагаемых в представлении 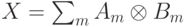 . Для этого зафиксируем некоторые ортонормированные базисы в пространствах
. Для этого зафиксируем некоторые ортонормированные базисы в пространствах 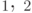 и выразим частичный след через матричные элементы
и выразим частичный след через матричные элементы  . Пусть
. Пусть  и
и 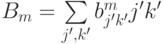 . Тогда
. Тогда
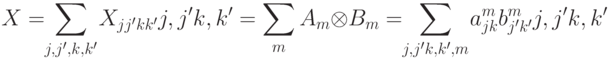

Рассмотрим пример, когда взятие частичного следа от матрицы плотности, соответствующей чистому состоянию, приводит к матрице плотности, соответствующей смешанному состоянию.
Пусть 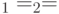 , а
, а 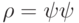 , где
, где 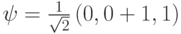 . В этом случае
. В этом случае 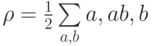 , поэтому получаем
, поэтому получаем
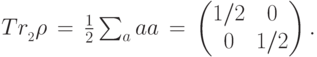
 и
и  имеют вероятности, равные
имеют вероятности, равные 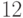 . Таким образом, отбрасывание второго q-бита приводит к чисто классическому распределению вероятностей на
первом q-бите.
. Таким образом, отбрасывание второго q-бита приводит к чисто классическому распределению вероятностей на
первом q-бите.Утверждение 9.1. Любое смешанное состояние  представимо как частичный след
представимо как частичный след 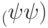 от чистого состояния большей системы,
от чистого состояния большей системы,  , причем можно считать, что
, причем можно считать, что  .
.
Доказательство. Полагаем 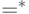 . Так как
. Так как  неотрицательно определена, то существует
неотрицательно определена, то существует 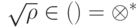 . Докажем, что для
. Докажем, что для 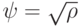 выполнено искомое, т.е.
выполнено искомое, т.е.  .
.
Поскольку  эрмитова, она диагонализуется в некотором ортонормированном базисе
эрмитова, она диагонализуется в некотором ортонормированном базисе 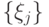 . Тогда
. Тогда  , а
, а 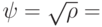
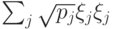 , и
, и  . Вклад в частичный след вносят лишь слагаемые с
. Вклад в частичный след вносят лишь слагаемые с 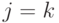 . Поэтому
. Поэтому 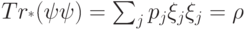 .
.
Задача 9.2. Пусть имеется чистое состояние  . Докажите, что существует так называемое разложение Шмидта:
. Докажите, что существует так называемое разложение Шмидта:
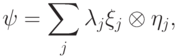
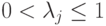 , а множества векторов
, а множества векторов 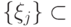 и
и 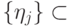 являются ортонормированными.
являются ортонормированными.Заметим, что числа 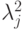 — это ненулевые собственные числа частичных следов
— это ненулевые собственные числа частичных следов 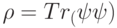 и
и 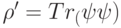 . (Таким образом, ненулевые собственные числа
. (Таким образом, ненулевые собственные числа  и
и 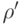 совпадают.) Отсюда следует, что взятие частичного следа от чистого состояния приводит к чистому состоянию тогда и только тогда, когда исходное состояние разложимо:
совпадают.) Отсюда следует, что взятие частичного следа от чистого состояния приводит к чистому состоянию тогда и только тогда, когда исходное состояние разложимо: 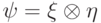 .
.
Задача 9.3. Пусть  — два чистых состояния, таких что
— два чистых состояния, таких что  . Докажите, что
. Докажите, что 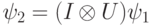 для некоторого унитарного оператора
для некоторого унитарного оператора  на пространстве
на пространстве  .
.

 задано
задано 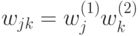 . Имеется два множества исходов
. Имеется два множества исходов 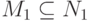 ,
, 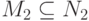 . Тогда вероятности перемножаются:
. Тогда вероятности перемножаются:  .
.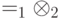 задана матрица плотности вида
задана матрица плотности вида  . Имеется два подпространства
. Имеется два подпространства 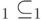 ,
, 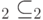 . Тогда вероятности также перемножаются:
. Тогда вероятности также перемножаются: 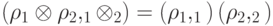 .
. . Интересующее нас событие не зависит от исхода во втором множестве:
. Интересующее нас событие не зависит от исхода во втором множестве: 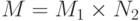 . Вероятность такого события выражается через проекцию распределения на первое множество:
. Вероятность такого события выражается через проекцию распределения на первое множество: 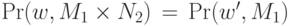 , где
, где 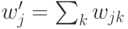 .
.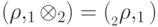 .
.