Класс NP: сводимость и полнота
Сводимость и NP-полнота.
Сложность вычисления предикатов можно сравнивать, пользуясь следующим определением.
Определение 2.4. Сводимость по Карпу. Предикат 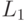 сводится к предикату
сводится к предикату 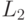 (обозначение
(обозначение 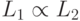 ), если существует такая функция
), если существует такая функция  , что
, что  .
.
Сводимость по Карпу также называют полиномиальной сводимостью, а часто — просто сводимостью.
Лемма 2.1. Пусть 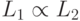 . Тогда
. Тогда


-
 .
.
Доказательство. Пункт 1 совершенно очевиден — чтобы вычислить значение предиката 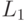 , достаточно применить ко входу
, достаточно применить ко входу  функцию
функцию  , а к результату ее работы — программу вычисления
, а к результату ее работы — программу вычисления 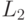 .
.
Пункт 3 также прост. Его можно объяснять по-разному. Например, так: Мерлин сообщает Артуру  (длина которого ограничена некоторым полиномом
(длина которого ограничена некоторым полиномом  от длины
от длины  , поскольку
, поскольку  ) и слово
) и слово  , которое убеждает Артура в том, что
, которое убеждает Артура в том, что  . Артур также может проверить, что ему действительно сообщено
. Артур также может проверить, что ему действительно сообщено  . Используя определение 2.2, можно написать цепочку эквивалентностей
. Используя определение 2.2, можно написать цепочку эквивалентностей
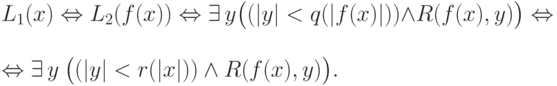
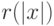 в последнем выражении — это композиция полиномов
в последнем выражении — это композиция полиномов  и
и  .
.Определение 2.5. Предикат 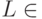 называется NP- полным, если любой предикат из
называется NP- полным, если любой предикат из  к нему сводится.
к нему сводится.
Если некоторый NP-полный предикат можно вычислять за время 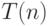 , то любой предикат из NP можно вычислять за время
, то любой предикат из NP можно вычислять за время 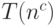 для некоторого фиксированного числа
для некоторого фиксированного числа  . Такая потеря эффективности считается в этой науке несущественной.
. Такая потеря эффективности считается в этой науке несущественной.
NP-полные предикаты существуют, приведем примеры.
Выполнимость. Задается предикатом
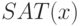

 есть формула с булевыми переменными и символами
есть формула с булевыми переменными и символами 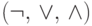 , которая истинна при некоторых значениях переменных.
, которая истинна при некоторых значениях переменных.
Теорема 2.2 (Кук, Левин). 1) 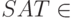 ; 2)
; 2) 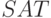 — NP- полна.
— NP- полна.
Если 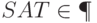 , то
, то  .
.
Доказательство (теоремы 2.2). 1) Мерлину достаточно сообщить Артуру значения переменных, входящих в формулу, при которых она истинна. Артур справится с проверкой истинности полученного высказывания.
2) Пусть предикат из NP, который нужно свести к 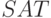 , имеет вид
, имеет вид 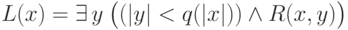 .
.
Рассмотрим таблицу вычисления (см. доказательство теоремы 1.2) для МТ, вычисляющей 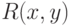 (входом является пара
(входом является пара  ). Будем использовать те же переменные, что и в доказательстве теоремы 1.2 (коды состояний клеток таблицы вычисления). Чтобы таблица вычисления соответствовала правильно проведенному успешному (с ответом "да") вычислению, должны выполняться локальные правила согласования для каждой четверки клеток вида
). Будем использовать те же переменные, что и в доказательстве теоремы 1.2 (коды состояний клеток таблицы вычисления). Чтобы таблица вычисления соответствовала правильно проведенному успешному (с ответом "да") вычислению, должны выполняться локальные правила согласования для каждой четверки клеток вида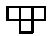 и результат должен быть "да". Каждое такое правило задается формулой от переменных, отвечающих либо рассматриваемой четверке, либо нулевой ячейке самой нижней строки таблицы. Определим формулу
и результат должен быть "да". Каждое такое правило задается формулой от переменных, отвечающих либо рассматриваемой четверке, либо нулевой ячейке самой нижней строки таблицы. Определим формулу 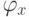 как конъюнкцию всех этих формул, в которые подставлены значения переменных, кодирующих вход
как конъюнкцию всех этих формул, в которые подставлены значения переменных, кодирующих вход  , дополненный символами
, дополненный символами  до длины
до длины 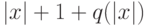 . Значения, соответствующие
. Значения, соответствующие  и
и  , — константы, поэтому переменные, от которых зависит эта формула, отвечают
, — константы, поэтому переменные, от которых зависит эта формула, отвечают  и кодам внутренних ячеек таблицы. Так что можно считать, что формула
и кодам внутренних ячеек таблицы. Так что можно считать, что формула 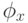 зависит от
зависит от  и еще от каких-то переменных, которые мы обозначим
и еще от каких-то переменных, которые мы обозначим  .
.
Итак, мы сопоставили слову  формулу
формулу 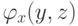 , которая по построению обладает следующим свойством. Если выполняется
, которая по построению обладает следующим свойством. Если выполняется 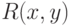 , то найдется такой набор значений
, то найдется такой набор значений 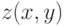 , при котором
, при котором  истинна (эти значения описывают работу МТ на входе
истинна (эти значения описывают работу МТ на входе  ). А если
). А если 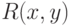 не выполняется, то
не выполняется, то 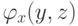 всегда ложна (поскольку по сути утверждает, что вычисление на входе
всегда ложна (поскольку по сути утверждает, что вычисление на входе  дает ответ "да"). Таким образом, при
дает ответ "да"). Таким образом, при  такая формула иногда (при некоторых значениях
такая формула иногда (при некоторых значениях  ) истинна, при
) истинна, при 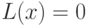 — всегда ложна.
— всегда ложна.
Другие примеры NP-полных задач получаются с помощью следующей леммы.
Лемма 2.2. Если  и
и 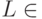 , то
, то  — NP-полная. И вообще, если
— NP-полная. И вообще, если 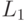 — NP-полная,
— NP-полная, 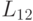 и
и  , то
, то 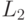 — NP-полная.
— NP-полная.
Доказательство. Достаточно проверить транзитивность сводимости: если 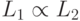 ,
, 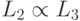 , то
, то 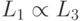 . Она следует из того, что композиция двух полиномиально вычислимых функций полиномиально вычислима.
. Она следует из того, что композиция двух полиномиально вычислимых функций полиномиально вычислима.


 есть 3-КНФ, которая истинна истинна при некоторых значениях переменных. 3-КНФ — это конъюнкция дизъюнкций, каждая из которых содержит три литерала.
есть 3-КНФ, которая истинна истинна при некоторых значениях переменных. 3-КНФ — это конъюнкция дизъюнкций, каждая из которых содержит три литерала.
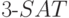 также NP-полна. Это устанавливается сведением к ней
также NP-полна. Это устанавливается сведением к ней 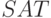 .
.
Теорема 2.3. 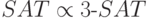 .
.
Доказательство. Сопоставим любой схеме в стандартном базисе такую 3-КНФ, выполнимость которой равносильна тому, что вычисляемая схемой функция не равна тождественно 0. В эту КНФ будут входить все переменные схемы ( 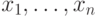 и
и 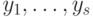 — используем те же обозначения, что и в определении схемы). Для этого построим вначале конъюнкцию
— используем те же обозначения, что и в определении схемы). Для этого построим вначале конъюнкцию 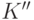 условий, означающих, что каждая из вспомогательных переменных
условий, означающих, что каждая из вспомогательных переменных 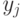 имеет значение, соответствующее правой части присваивания
имеет значение, соответствующее правой части присваивания 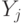 . Есть три типа таких условий (они соответстуют трем базисным функциям), и каждый можно записать в виде 3-КНФ:
. Есть три типа таких условий (они соответстуют трем базисным функциям), и каждый можно записать в виде 3-КНФ:
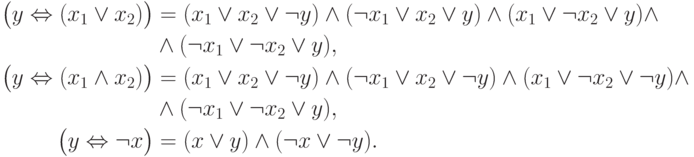
Подставляя эти 3-КНФ в 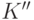 , получим 3-КНФ
, получим 3-КНФ  . Искомая 3-КНФ имеет вид
. Искомая 3-КНФ имеет вид 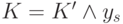 . Действительно, истинность
. Действительно, истинность  равносильна утверждению: все присваивания выполнены правильно и в результате получилась 1 (
равносильна утверждению: все присваивания выполнены правильно и в результате получилась 1 ( 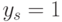 ). Значит, если при каких-то значениях переменных
). Значит, если при каких-то значениях переменных  схема выдает 1, то
схема выдает 1, то  выполнима, и наоборот.
выполнима, и наоборот.
Еще один простой пример сведения.
Задача ЦЛП (целочисленного линейного программирования). Дана система линейных неравенств с целыми коэффициентами. Есть ли у нее целочисленное решение? (Другими словами, совместна ли система?)
В этой задаче входом является матрица коэффициентов и вектор правых частей. То, что 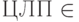 , не совсем очевидно. Оказывается, что в качестве подсказки Мерлин может сообщить Артуру значения переменных, при которых выполнены все неравенства системы. По определению, длина этого сообщения должна быть также полиномиально ограничена. Можно доказать, что из существования целочисленного решения следует существование целочисленного решения, размер записи которого ограничен полиномом от длины записи системы, см. [14, т. 2, 17.1].
, не совсем очевидно. Оказывается, что в качестве подсказки Мерлин может сообщить Артуру значения переменных, при которых выполнены все неравенства системы. По определению, длина этого сообщения должна быть также полиномиально ограничена. Можно доказать, что из существования целочисленного решения следует существование целочисленного решения, размер записи которого ограничен полиномом от длины записи системы, см. [14, т. 2, 17.1].
Сведем теперь 3-КНФ к ЦЛП. Построим по 3-КНФ систему линейных неравенств. Целочисленных переменных возьмем столько же, сколько есть булевых переменных. Булевой переменной  сопоставим выражение
сопоставим выражение 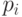 . Отрицанию переменной
. Отрицанию переменной  сопоставим выражение
сопоставим выражение 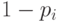 . Каждой дизъюнкции
. Каждой дизъюнкции 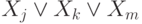 (
(  — литералы) сопоставим неравенство
— литералы) сопоставим неравенство 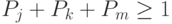 , в котором
, в котором 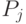 ,
, 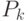 ,
, 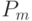 — выражения, сопоставленные литералам дизъюнкции.
— выражения, сопоставленные литералам дизъюнкции.
Искомая система содержит для всех  неравенства
неравенства  , а также все неравенства, сопоставленные дизъюнкциям из КНФ. Очевидно, что выполнимость 3-КНФ равносильна совместности такой системы.
, а также все неравенства, сопоставленные дизъюнкциям из КНФ. Очевидно, что выполнимость 3-КНФ равносильна совместности такой системы.
Замечание 2.4. Если не требовать целочисленности решений, то проверить совместность системы линейных неравенств можно за полиномиальное время. Примеры таких алгоритмов (Хачияна, Кармаркара) также см. в [14, т. 1, 13, 15.1].
Обширный список NP-полных задач содержится в книге Гэри и Джонсона [3]. Как правило, их NP-полнота доказывается с помощью сведений. Приведем несколько примеров NP-полных задач.
3-раскраска. Дан граф. Спрашивается, можно ли раскрасить его вершины в три цвета так, чтобы концы каждого ребра были покрашены в разные цвета. (Аналогичная задача 2-раскраска решается за полиномиальное время.)
Клика. Даны граф и число  . Спрашивается, есть ли
. Спрашивается, есть ли  -элементное множество вершин графа, любые две вершины которого соединены ребром.
-элементное множество вершин графа, любые две вершины которого соединены ребром.
Задачи
- Докажите, что задача проверки выполнимости 2-КНФ (конъюнкции дизъюнкций, каждая из которых содержит два литерала) принадлежит P.
- Докажите, что задача об эйлеровом пути в неориентированном графе (существует ли путь, проходящий по всем ребрам ровно по одному разу) принадлежит P.
- Предположим, что класс NP совпадает с P. Докажите, что в этом случае за полиномиальное время можно не только проверить выполнимость формулы, но и найти значения переменных, при которых она истинна (аналогично для гамильтонова цикла и т.п.)
- Докажите, что задача о паросочетаниях (есть
 мальчиков и
мальчиков и  девочек, известно, какие пары согласны друг с другом танцевать; надо определить, можно ли устроить танец, в котором все
девочек, известно, какие пары согласны друг с другом танцевать; надо определить, можно ли устроить танец, в котором все  мальчиков и
мальчиков и  девочек соединены в пары) принадлежит NP и, более того, принадлежит P.
девочек соединены в пары) принадлежит NP и, более того, принадлежит P. -
Постройте
- полиномиальное сведение задачи 3-КНФ к задаче Клика;
- тот же вопрос, но дополнительно требуется, чтобы количество решений сохранялось (если 3-КНФ
 при сведении соответствует пара (граф
при сведении соответствует пара (граф  , размер
, размер  ), то количество выполняющих наборов переменных для
), то количество выполняющих наборов переменных для  равно количеству клик размера
равно количеству клик размера  в графе
в графе  ).
).
-
Постройте
- полиномиальное сведение задачи 3-КНФ к задаче 3-раскраска;
- тот же вопрос, но дополнительно требуется, чтобы количество выполняющих наборов переменных для любой 3-КНФ равнялось бы шестикратному количеству 3-раскрасок соответствующего ей графа.
- Покажите, что следующая задача является NP-полной: дан набор из не более чем
 типов квадратиков
типов квадратиков  , на сторонах которых написаны какие-то буквы; дан список допустимых пар букв и список граничных букв; спрашивается, можно ли корректно сложить из квадратиков набора большой квадрат размера
, на сторонах которых написаны какие-то буквы; дан список допустимых пар букв и список граничных букв; спрашивается, можно ли корректно сложить из квадратиков набора большой квадрат размера  (так, чтобы на примыкающих сторонах квадратиков были только допустимые пары букв, а на границе квадрата — только граничные буквы).
(так, чтобы на примыкающих сторонах квадратиков были только допустимые пары букв, а на границе квадрата — только граничные буквы). - Докажите, что предикат "
 — двоичная запись составного числа" принадлежит NP.
— двоичная запись составного числа" принадлежит NP. - Докажите, что предикат "
 — двоичная запись простого числа" принадлежит NP.
— двоичная запись простого числа" принадлежит NP.
