Что такое алгоритм?
Задачи
- Постройте машину Тьюринга, которая записывает входное двоичное слово в обратном порядке.
- Постройте машину Тьюринга, которая складывает два числа, записанные в двоичной системе. Для определенности считайте, что записи чисел разделены специальным символом алфавита "
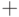 ".
". - Докажите, что не существует алгоритма, который по машине Тьюринга и входу определяет, остановится ли она на этом входе.
- Докажите, что не существует алгоритма, который выписывает одну за другой все машины Тьюринга, которые не останавливаются, будучи запущенными на пустой ленте.
-
Пусть
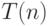 — максимальное время, которое может пройти до остановки машины Тьюринга с
— максимальное время, которое может пройти до остановки машины Тьюринга с  состояниями и
состояниями и  символами алфавита, если ее запустить на пустой ленте. Докажите, что функция
символами алфавита, если ее запустить на пустой ленте. Докажите, что функция 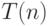 растет быстрее любой вычислимой всюду определенной функции
растет быстрее любой вычислимой всюду определенной функции  , то есть
, то есть ![\lim [T(n)/b(n)]=+\infty](/sites/default/files/tex_cache/234248c544a0424d4e328ff829bd19fd.png) .
.Набор элементарных инструкций у описанных выше машин Тьюринга крайне беден. Имеются разнообразные их обобщения, например, многоленточные машины Тьюринга. В отличие от описанной выше, такая МТ имеет несколько (конечное множество) лент, каждая со своей головкой, управляющему устройству доступны символы, находящиеся в ячейках, на которых расположены головки лент. Выделены две ленты: входная, с которой разрешается только читать символы, и выходная, на которую разрешается только писать символы. Остальные ленты называются рабочими. Многоленточная машина называется
 -ленточной, если у нее
-ленточной, если у нее  рабочих лент. Действие за такт работы состоит в изменении состояния управляющего устройства, изменении символов в ячейках под головками и изменении положений головок на лентах (каждая головка сдвигается не более, чем на одну позицию). Это действие однозначно определяется состоянием управляющего устройства и набором символов в ячейках под головками. Если действие выполнить нельзя, машина останавливается.
рабочих лент. Действие за такт работы состоит в изменении состояния управляющего устройства, изменении символов в ячейках под головками и изменении положений головок на лентах (каждая головка сдвигается не более, чем на одну позицию). Это действие однозначно определяется состоянием управляющего устройства и набором символов в ячейках под головками. Если действие выполнить нельзя, машина останавливается.В начале работы многоленточной машины Тьюринга все ленты пусты, кроме входной, на которой записан вход. Результат работы машины — состояние выходной ленты в конце работы.
Если интересоваться сложностью алгоритмов с точностью до полиномиально ограниченного множителя, многоленточные машины ничего не добавляют по сравнению с описанными выше машинами с единственной лентой.
- Докажите, что двухленточную машину Тьюринга, работающую за время
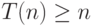 на входах длины
на входах длины  , можно моделировать на машине с единственной лентой за время
, можно моделировать на машине с единственной лентой за время 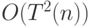 .
. - Докажите, что трехленточную машину Тьюринга, работающую за время
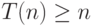 на входах длины
на входах длины  , можно моделировать на двухленточной за время
, можно моделировать на двухленточной за время  .
. - Пусть
 — машина Тьюринга с единственной лентой, которая копирует входное слово (приписывая его копию справа от самого слова). Пусть
— машина Тьюринга с единственной лентой, которая копирует входное слово (приписывая его копию справа от самого слова). Пусть 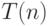 — максимальное время ее работы на входах длины
— максимальное время ее работы на входах длины  . Докажите, что
. Докажите, что  для некоторого
для некоторого  и для всех
и для всех  . Что можно сказать про
. Что можно сказать про 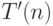 , которое есть минимальное время ее работы на входах длины
, которое есть минимальное время ее работы на входах длины  ?
? - Рассмотрим язык программирования, в котором есть всего
 натуральных переменных, разрешенные операции — прибавление и вычитание
натуральных переменных, разрешенные операции — прибавление и вычитание  , разрешенная проверка — не равна ли переменная нулю. Разрешено использовать if-then-else и while, но рекурсия не разрешена. Докажите, что с помощью программ на таком языке программирования можно вычислять любую вычислимую функцию.
, разрешенная проверка — не равна ли переменная нулю. Разрешено использовать if-then-else и while, но рекурсия не разрешена. Докажите, что с помощью программ на таком языке программирования можно вычислять любую вычислимую функцию. - Постройте алгоритм, определяющий, является ли данный базис полным. Базисные функции заданы таблицами значений.
- Пусть
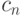 есть максимум сложности
есть максимум сложности 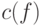 по всем булевым функциям
по всем булевым функциям  от
от  переменных. Докажите, что
переменных. Докажите, что 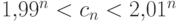 при достаточно больших
при достаточно больших  .
. -
Глубиной схемы называется максимальное число элементов на пути от входов к выходу. Покажите, что любую функцию можно вычислить схемой глубины не более
 из элементов
из элементов  и из элементов
и из элементов  и
и  с произвольным числом входов.
с произвольным числом входов. - Докажите, что если из схемы глубины
 , вычисляющей функцию
, вычисляющей функцию 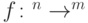 , выбросить все несущественные присваивания, то полученная схема имеет полиномиальный по
, выбросить все несущественные присваивания, то полученная схема имеет полиномиальный по 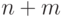 размер.
размер. - Постройте схему, которая сравнивает два
 -битовых числа и имеет размер
-битовых числа и имеет размер  , а глубину
, а глубину  .
. -
- Постройте схему сложения двух
 -битовых чисел размера
-битовых чисел размера  .
. - Тот же вопрос, если дополнительно потребовать, чтобы глубина схемы была
 .
.
- Постройте схему сложения двух
- Функция
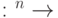 равна 1 на двоичных словах, в которых число единиц больше числа нулей, и 0 — на остальных словах. Постройте схему, вычисляющую эту функцию, размер схемы должен быть линеен по
равна 1 на двоичных словах, в которых число единиц больше числа нулей, и 0 — на остальных словах. Постройте схему, вычисляющую эту функцию, размер схемы должен быть линеен по  , глубина —
, глубина —  .
. - Постройте схему размера
 и глубины
и глубины 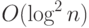 , которая проверяет, связаны ли путем две вершины в графе. Граф на
, которая проверяет, связаны ли путем две вершины в графе. Граф на  вершинах, которые помечены числами от 1 до
вершинах, которые помечены числами от 1 до  , задается
, задается 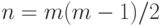 булевыми переменными. Переменная
булевыми переменными. Переменная 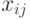 , где
, где  , определяет, есть ли в графе ребро, соединяющее вершины
, определяет, есть ли в графе ребро, соединяющее вершины  и
и  .
. - Пусть схема глубины
 из элементов
из элементов  и из элементов
и из элементов  и
и  с произвольным числом входов вычисляет сложение
с произвольным числом входов вычисляет сложение  битов по модулю
битов по модулю  (функция
(функция  ). Покажите, что размер схемы не меньше
). Покажите, что размер схемы не меньше 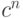 для некоторого
для некоторого  .
. -
Пусть
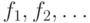 — последовательность булевых функций от
— последовательность булевых функций от 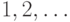 аргументов. Покажите, что следующие два свойства равносильны:
аргументов. Покажите, что следующие два свойства равносильны:- существует последовательность вычисляющих эти функции формул, размер которых не превосходит полинома от
 ;
; - существует последовательность вычисляющих эти функции схем глубины
 из элементов
из элементов  ,
,  и
и  (с двумя входами).
(с двумя входами).
- существует последовательность вычисляющих эти функции формул, размер которых не превосходит полинома от
- Докажите, что существует разрешимый предикат, который принадлежит
 , но не принадлежит
, но не принадлежит  .
.
