Введение в математическое программирование
[+]
Донецкий национальный технический университет
Опубликован: 09.07.2007 | Доступ: свободный | Студентов: 3116 / 711 | Оценка: 4.34 / 4.12 | Длительность: 13:54:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Программист
Теги: beta, анализ, базисное решение, вычисления, двойственная задача, задача линейного программирования, законы, искусственная жизнь, исследования, метод полного исключения, моделирование, нелинейное программирование, оптимальный план, поиск, программирование, симплекс, симплекс-метод, функция лагранжа, экстремум функции, электронная почта, элементы

Лекция 7: Нелинейное программирование. Классификация методов нелинейного программирования. Классический метод определения условного экстремума. Метод множителей Лагранжа

A
|
версия для печати
< Лекция 6 || Лекция 7: 1234 || Лекция 8 >

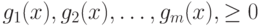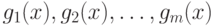Теорема 3.6 (о выпуклости допустимого множества решений). Пусть g_1(x),g_2(x),\ldots,g_m(x), \ge 0 и x \ge 0 - ограничения задачи нелинейного программирования. Если функции g_1(x),g_2(x),\ldots,g_m(x) - вогнуты, то допустимое множество 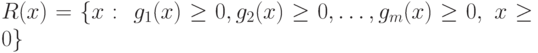R(x)= \{ x: \; g_1(x) \ge 0, g_2(x) \ge 0, \ldots, g_m(x) \ge 0, \; x \ge 0 \} является выпуклым.

Доказательство. Для доказательства теоремы достаточно показать, что множество R(x)= \{ x: \; g_1(x) \ge 0,\; x \ge 0 \} при каждом i = \overline{1,m} будет выпуклым. Тогда множество R=R_1 \cap R_2 \cap \ldots \cap R_m также выпукло, так как пересечение конечного числа выпуклых множеств Ri.

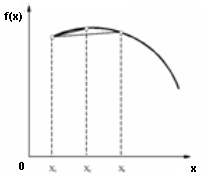
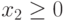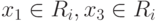Рассмотрим некоторую вогнутую функцию g_i(x) \ge 0. Выберем две произвольных точки x_1 \ge 0 и x_2 \ge 0 (рис.7.1). Тогда x_2 = \lambda x_1 + (1 - \lambda) x_3 \ge 0 , \; 0 < \lambda < 1. Поскольку x_1 \in R_i, x_3 \in R_i, то и точка x2 принадлежит Ri. Из условия вогнутости gi следует, что g_i[\lambda x+1 +(1 - \lambda)] \ge g_i (x_1) \lambda + (1 - \lambda) g_i(x_1) \ge 0.

Следовательно, множество Ri содержит отрезок 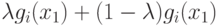\lambda g_i(x_1) + (1-\lambda) g_i(x_1), и поэтому оно выпукло (рис.7.1).


Рис. 7.1.

Справедливое такое утверждение: если функции 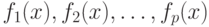f_1(x),f_2(x),\ldots,f_p(x) - выпуклы (вогнуты) на множестве Ri, то функция g(x)=\sum_{i=1}^p k_i f_i(x) - также выпукла (вогнута) при условии, что все k_i \ge 0, \; i=1,2,\ldots,p.

Рассмотрим метод поиска условного экстремума. Он состоит из следующих процедур.

1.Отыскивают множество всех стационарных точек S1(x) функции f(x) на выпуклом допустимом множестве R. Найденные точки далее исследуют на максимум (минимум) и определяют точку наибольшего максимума 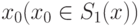x_0(x_0 \in S_1(x)).

2. Переходят к исследованию точек границы S2(x) и отысканию тех из них, где f(x) достигает максимума. Этот процесс состоит в следующем. Выбирают произвольную границу, определяемую, например, условием g1(x)=0. Если функция

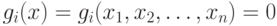g_i(x) = g_i(x_1, x_2, \ldots, x_n) = 0 ( 3.7)
является сепарабельной, то можно, определив из (3.7) переменную
x_i = \varphi(\{ x_j \}), \; j = \overline{1,n} , \; j \neq i
подставить ее в выражение для f(x). Тем самым задача сведется к поиску безусловного экстремума, для чего можно использовать процедуру, описанную в п.1.

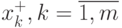Обозначим через x_i^+ точку границы g_i(x)=0, \; x_i^+ \in R, в которой f(x) достигает максимума. Повторив вышеописанную процедуру по всем остальным границам, найдем соответственно точки максимума (минимума) для всех границ x_k^+, k = \overline{1,m}.

3. Непосредственным сравнением значений функции f(x) для всех точек 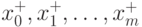x_0^+,x_1^+,\ldots,x_m^+ определяют точку абсолютного максимума (минимума) xopt на множестве решений R.

Такой подход требует значительных вычислительных затрат и может применяться лишь в простейших случаях при небольшом числе ограничений m и для случая сепарабельных функций g1(x), поэтому область его применения очень ограничена, и ниже рассматриваются более эффективные методы решения задач условной оптимизации.

Обобщение понятия выпуклой функции. Рассмотрим некоторые классы функций, которые не являются полностью выпуклыми, но обладают лишь отдельными их свойствами.

Определение 3.5. Пусть функция f(x) определена на непустом и выпуклом множестве R. Функция f(x) квазивыпукла, если для любых 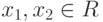x_1, x_2 \in R и \lambda \in [0,1] выполняется неравенство

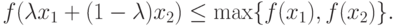f(\lambda x_1 + (1-\lambda)x_2) \le \max \{ f(x_1), f(x_2) \}. ( 3.8)

Функция f(x) называется квазивогнутой, если -f(x) - квазивыпуклая функция.

Из этого определения следует, что функция f(x) - квазивыпукла, если из неравенства f(x_2) \ge f(x_1) следует, что f(x2) не меньше значения функции f(x) в любой точке, являющейся выпуклой комбинацией точек x1 и x2. И наоборот, функция f(x) квазивогнута, если из неравенства f(x_2) \ge f(x_1) следует, что f(x1) не больше значения f(x) в любой точке, которая есть выпуклой комбинацией точек x1 и x2.

На рис. 7.2 приведены примеры квазивыпуклых и квазивогнутых функций, где а - квазивыпуклая, б - квазивогнутая функции.

Введем понятия строгой квазивыпуклости и квазивогнутости.


Рис. 7.2.

Определение 3.6. Пусть функция f(x) определена на непустом и выпуклом множестве R. Функция f(x) строго квазивыпукла, если для любых 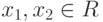x_1, x_2 \in R таких, что f(x_1) \neq f(x_2) и \lambda \in (0;1) выполняется неравенство

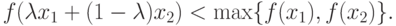f(\lambda x_1 +(1-\lambda)x_2) < \max \{ f(x_1), f(x_2) \}. ( 3.9)

Функция f(x) называется строго квазивогнутой, если -f(x) - строго квазивыпуклая функция. На рис. 7.3 изображены: а, б - строго квазивыпуклые функции, в - квазивогнутая функция. Из приведенного определения следует, что любая выпуклая функция является в тоже время и строго квазивыпуклой.

Строго квазивыпуклые и квазивогнутые функции играют важную роль в нелинейном программировании, поскольку для них локальный минимум и локальный максимум являются глобальным минимумом и максимумом соответственно.


Рис. 7.3.

Утверждение. Пусть f(x) - строго квазивыпуклая функция. Рассмотрим задачу минимизаци f(x) при условии, что x \in R, где R - непустое выпуклое множество в E(n). Пусть \overline{x} - точка локального минимума рассматриваемой задачи. Тогда она является и точкой глобального минимума.

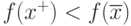Доказательство. Предположим противное, то есть пусть существует точка x^+ \in R, для которой f(x^+) < f(\overline{x}). Поскольку R - выпуклое, то точка \lambda x^+ + (1-\lambda)\overline{x} \in R при любой \lambda \in (0;1). Так как \overline{x} - точка локального минимума, то

f(\overline{x}) \le f [\lambda x^+ + (1-\lambda) \overline{x} ] ( 3.10)
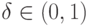для всех \lambda \in (0, \delta) для некоторого \delta \in (0,1).

Поскольку f(x) - квазивыпуклая функция и выполняется неравенство 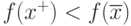f(x^+) < f(\overline{x}), то мы получим, что f[\lambda x^+ + (1-\lambda)\overline{x} ]< f(\overline{x}) при всех \labda \in (0;1). Однако это соотношение противоречит (3.10).

Заметим, что строго квазивыпуклые и квазивогнутые функции называются унимодальными.

Дальше >>
< Лекция 6 || Лекция 7: 1234 || Лекция 8 >

Вопросы и ответы

вопросов: 0