Введение в математическое программирование
[+]
Донецкий национальный технический университет
Опубликован: 09.07.2007 | Доступ: свободный | Студентов: 3134 / 727 | Оценка: 4.34 / 4.12 | Длительность: 13:54:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Программист
Теги: beta, анализ, базисное решение, вычисления, двойственная задача, задача линейного программирования, законы, искусственная жизнь, исследования, метод полного исключения, моделирование, нелинейное программирование, оптимальный план, поиск, программирование, симплекс, симплекс-метод, функция лагранжа, экстремум функции, электронная почта, элементы

Лекция 4: Метод полного исключения. Табличный симплекс – метод. Геометрическая интерпретация задач линейного программирования

A
|
версия для печати
< Лекция 3 || Лекция 4: 123 || Лекция 5 >

3. Геометрическая интерпретация задач линейного программирования

Рассмотрим такой пример:

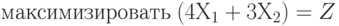
\text{максимизировать} \; (4Х_1 + 3Х_2 ) = Z
при условиях
X_1 \leq 4000; \; X_2 \leq 6000; \; X_1 + 2/3X_2 \leq 6000; \; X_1, X_2 \geq 0


Рис. 4.1.

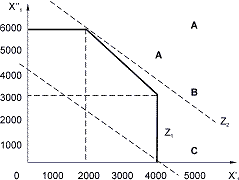
Каждое из этих неравенств определяет полуплоскости, пересечение которых дает многоугольник, заштрихованый на рис. 4.1. Этот многоугольник (выпуклый многогранник) и представляет собой допустимое множество решений R(x1, x2) задачи ЛП. Теперь рассмотрим целевую функцию

f(x1,x2)=4x1+3x2,

пусть ее значения

f(x1,x2)=12000=Z1.

График уравнения 4х1+3х2=12000 - прямая с отрезками на осях x1=3000; x2=4000.

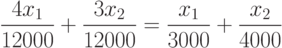
\frac{4x_1}{12000} + \frac{3x_2}{12000} = \frac{x_1}{3000} + \frac{x_2}{4000}
При f(x1,x2)=24000 получим прямую z2.

Прямая z2 параллельная прямой z1, но расположена выше от нее. Передвигая прямую z вверх параллельно самой себе, приходим к такому ее положению, когда прямая и множество R будут иметь только одну общую точку А.

Очевидно, что точка А (x1=2000; x2=6000) - оптимальное решение, так как она лежит на прямой с максимально возможным значением z_{\max}. Заметим, что эта точка оказалась крайней точкой множества R.

При векторной форме ограничения задачи ЛП записываются так:

A_1 x_1 + A_2 x_2 + . + A_n x_n \leq b, ( 3.1)
где
A_1 = \left[ \begin{gathered} a_{11} \\ a_{12} \\ \ldots \\ a_{m1} \end{gathered} \right] , \; A_2 = \left[ \begin{gathered} a_{21} \\ a_{22} \\ \ldots \\ a_{m2} \end{gathered} \right] , \; . , \; A_n = \left[ \begin{gathered} a_{21} \\ a_{22} \\ \ldots \\ a_{mn} \end{gathered} \right] .

Рассмотрим допустимое множество A1, A2,.,An в пространстве данных векторов. Поскольку в формуле (3.1) х_і \geq 0, \; i = 1,2, ..., n, то все положительные комбинации векторов A1,A2,.,An образуют конус. Поэтому вопрос о существовании допустимых решений равнозначен вопросу о принадлежности вектора b этому конусу. Поскольку A1,A2,.,An m -мерные векторы (n > m), то среди них всегда обнаружится m линейно-независимых векторов, образующих базис m -мерного пространства и содержащих конус, образованный векторами A1,A2,.,An...

Поэтому справедливо следующее утверждение. Если задача ЛП содержит n переменных и m ограничений, записанных в форме неравенств (n > m), не считая ограничений неотрицательности переменных x_i \geq 0, то в оптимальное решение входит не более чем m ненулевых компонент вектора x.

Расширенная форма задачи ЛП. Для решения задач ЛП необходимо переходить от ограничений - неравенств к ограничениям в форме уравнений. Для этого в каждое неравенство вводят по одной свободной переменной x_{n+1} \geq 0, x_{n+2} \geq 0,.,x_{n+m} \geq 0, чтобы превратить его в равенство. В таком виде задачу ЛП называют расширенной и записывают так:

\begin{multiple} \text{максимизировать}\\ f(x_1, x_2, ., x_n) = c_1 x_1 + c_2 x_2 + \ldots + c_n x_n + 0x_{n+m} \end{multiple} ( 3.2)
при ограничениях

a11x1+a12x2+.+a1nxn+1xn+1+0xn+2+...+0xn+m=b1;
a21x1+a22x2+.+a2nxn+0xn+1+1xn+2+...+0xn+m=b2;
........................................
am1x1+am2x2+.+amnxn+0xn+1+0xn+2+...+1xn+m=bm ...

В матричной форме эта задача имеет следующий вид:

\text{максимизировать} \; c^T x
при ограничениях
A^{m \times n} x_1 + E^{m \times m} x_2 = b;
где
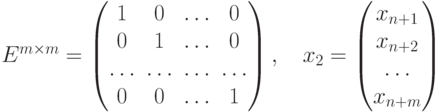E^{m \times m} = \begin{pmatrix} 1 &0 &\ldots &0 \\ 0 &1 &\ldots &0 \\ \ldots &\ldots &\ldots &\ldots \\ 0 &0 &\ldots &1 \end{pmatrix}, \quad x_2 = \begin{pmatrix} x_{n+1} \\ x_{n+2} \\ \ldots \\ x_{n+m} \end{pmatrix} ( 3.3)

Наконец, векторная форма записи расширенной задачи ЛП:

\text{максимизировать} \; c^T x
при ограничениях
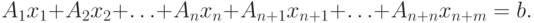A_1 x_1 + A_2 x_2 + \ldots + A_n x_n + A_{n+1} x_{n+1} +\ldots+ A_{n+n} x_{n+m} = b. ( 3.4)


Рис. 4.2.

Рис. 4.3.

Пусть R и R1 - допустимые множества решений исходной и расширенной задач соответственно. Тогда любой точке допустимого множества решений R1 соответствует единственная точка множества R, и наоборот.

Установим отношение между элементами R и R1:

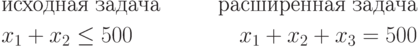
\begin{align*} & \text{исходная задача} & \text{расширенная задача} \\ & x_1 + x_2 \leq 500 & x_1 + x_2 + x_3 = 500 \end{align*}

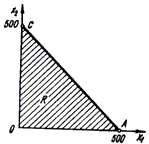
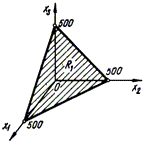
На рис. 4.2 и 4.3 изображены допустимые множества решений обеих задач. Очевидно, что треугольник ОСА (рис. 4.2) - допустимое множество R - есть проекция допустимого множества R1 (рис.4.3) на подпространство x_1 \cup x_2.

В общем случае допустимое множество решений исходной задачи R есть проекция допустимого множества решений расширенной задачи R1 на подпространство исходных переменных x_1 \cup x_2.

Дальше >>
< Лекция 3 || Лекция 4: 123 || Лекция 5 >

Вопросы и ответы

вопросов: 0