Московский физико-технический институт
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3974 / 1245 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00
ISBN: 978-5-9556-0065-9
Специальности: Программист, Математик
Теги:
Лекция 3:
Численное решение систем линейных алгебраических уравнений
2.6. Вариационные итерационные методы
2.6.1. Связь между вариационной задачей и задачей решения СЛАУ
Пусть 
, где Ln есть n -мерное евклидово пространство. Рассмотрим квадратичный функционал
от 
, называемый функционалом энергии:
где 
— линейный оператор, 
, c — константа. Этот функционал совпадает с квадратичным функционалом 
, где 
— сопряженный к оператор. Действительно, 
по определению сопряженного оператора и 
в силу коммутативности скалярного произведения. Тогда
Без ограничения общности предположим, что оператор — самосопряженный, 
В противном случае будем рассматривать задачу с оператором
Будем также считать, что — положительный
оператор, т.е.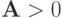 
, это означает, что для любого
ненулевого вектора выполнено 
Поставим задачу об отыскании элемента 
, придающего наименьшее значение функционалу 
:
Теорема. Пусть 
В этом случае существует единственный элемент 
, придающий наименьшее значение квадратичному функционалу 
, являющийся решением СЛАУ 
Доказательство.
СЛАУ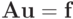 
имеет единственное решение , поскольку является невырожденным оператором в силу его положительной определенности. Покажем, что в этом случае при 
для любого вектора 
имеет место 
, т.е. при 
достигается
минимум квадратичного функционала 
Действительно,
![\begin{gather*}
\Phi (\mathbf{v} + \mathbf{\Delta }) = (\mathbf{A}(\mathbf{v} + \mathbf{\Delta }), \mathbf{v} + \mathbf{\Delta }) - 2(\mathbf{f,v} + \mathbf{\Delta }) + c = \\
= (\mathbf{Av} + \mathbf{A\Delta }\mathbf{,v} + \mathbf{\Delta }) - 2(\mathbf{f,v} + \mathbf{\Delta }) + c = \\
= (\mathbf{Av,v}) + (\mathbf{Av}\mathbf{,\Delta }) + (\mathbf{A\Delta }
\mathbf{,v}) + (\mathbf{A\Delta }\mathbf{,\Delta }) - 2(\mathbf{f}\mathbf{,v}) - 2(\mathbf{f}\mathbf{,\Delta }) + c = \\
= (\mathbf{Av}\mathbf{,v}) + 2(\mathbf{Av}\mathbf{,\Delta }) + (\mathbf{A\Delta }\mathbf{,\Delta }) - 2(\mathbf{f}\mathbf{,v}) - 2(\mathbf{f}\mathbf{,\Delta }) + c = \\
= \left[{(\mathbf{Av}\mathbf{,v}) - 2(\mathbf{f}\mathbf{,v}) + c}\right] + 2(\mathbf{Av}\mathbf{,\Delta }) - 2(\mathbf{f}\mathbf{,\Delta }) + (\mathbf{A\Delta }\mathbf{,\Delta }) = \\
= \Phi (\mathbf{v}) + 2(\mathbf{Av}-\mathbf{f},\mathbf{\Delta }) + (\mathbf{A\Delta }\mathbf{,\Delta }) = \Phi (\mathbf{v}) + (\mathbf{A\Delta }\mathbf{,\Delta }) > \Phi (\mathbf{v}),
\end{gather*}](/sites/default/files/tex_cache/cc0054fb6168f7015521d17fef538ef4.png)
т.е. при 
и любом имеет место 
Докажем, что верно и обратное утверждение. Если элемент доставляет минимальное значение функционалу энергии, то он является решением системы линейных уравнений 
Из курса математического анализа известно, что в точке минимума должно выполняться условие 
Вычисляя градиент, приходим к условию минимума функционала 
Таким образом установлена эквивалентность вариационной задачи (отыскание элемента, придающего минимум ) и задачи о нахождении решения СЛАУ.
Заметим, что СЛАУ с самосопряженным и положительно определенным оператором представляют собой важный класс задач в математической физике, в частности, они возникают при решении краевых задач для эллиптических уравнений. При необходимости можно произвести симметризацию по Гауссу исходной системы.
