Численное решение систем линейных алгебраических уравнений
2.7. О спектральных задачах
Спектральные задачи — вычислительно наиболее трудоемкие задачи в прикладной линейной алгебре. Различают полную и частичную проблемы собственных значений. В первом случае необходимо отыскать ВСЕ собственные числа матрицы, во втором — лишь максимальное по абсолютной величине собственное число. Различают также самосопряженную спектральную задачу и задачу для произвольной матрицы. Очевидно, самосопряженная проблема решается проще — спектр самосопряженной матрицы всегда действительный.
Рассмотрим два алгоритма для самосопряженных матриц. Первый — степенной алгоритм, для вычисления наибольшего по абсолютной величине собственного числа. Выбираем произвольный ненулевой вектор 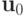 и строим последовательность векторов
и строим последовательность векторов

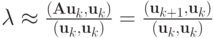
приближает максимальное по абсолютной величине собственное значение с точностью  Здесь
Здесь 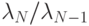 — отношение самого большого по модулю собственного числа матрицы к следующему по абсолютной величине.
— отношение самого большого по модулю собственного числа матрицы к следующему по абсолютной величине.
Для решения полной самосопряженной проблемы собственных значений применяется метод вращений.
Определение собственных значений самосопряженной матрицы  эквивалентно отысканию такой ортогональной матрицы
эквивалентно отысканию такой ортогональной матрицы  , что
, что
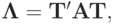
матрица  — диагональная. Среди всех ортогональных преобразований данное минимизирует сумму квадратов внедиагональных
элементов исходной матрицы. Построим итерационный метод, минимизирующий эту сумму на каждой итерации. Пусть каждое преобразование подобия на каждой итерации содержит лишь одну матрицу вращения
— диагональная. Среди всех ортогональных преобразований данное минимизирует сумму квадратов внедиагональных
элементов исходной матрицы. Построим итерационный метод, минимизирующий эту сумму на каждой итерации. Пусть каждое преобразование подобия на каждой итерации содержит лишь одну матрицу вращения  , где матрица
, где матрица 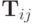 есть матрица поворота в плоскости
есть матрица поворота в плоскости 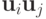 на угол
на угол  Эта матрица отличается от матрицы
Эта матрица отличается от матрицы  только двумя строками и двумя столбцами (с номерами i и j ). Так как евклидова норма матрицы не изменяется при ортогональных преобразованиях, то легко получить соотношение между суммами квадратов внедиагональных элементов старой и новой матриц:
только двумя строками и двумя столбцами (с номерами i и j ). Так как евклидова норма матрицы не изменяется при ортогональных преобразованиях, то легко получить соотношение между суммами квадратов внедиагональных элементов старой и новой матриц:
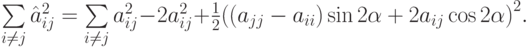
Очевидны условия минимизации суммы в левой части последнего равенства. Следует на текущей итерации выбирать индексы так, чтобы выполнялось условие 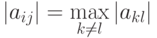 , а угол поворота выбирается из условия
, а угол поворота выбирается из условия  Тогда он удовлетворяет условию
Тогда он удовлетворяет условию
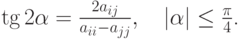
Независимо от наличия кратных собственных значений метод вращений обладает квадратичной сходимостью.
Выбор максимального по модулю внедиагонального элемента — затратная операция, поэтому часто реализуется метод вращений с барьерами. Его идея состоит в следующем. При переборе внедиагональных значений вращение производится тогда, когда значение элемента по абсолютной величине превосходит некоторую величину (барьер). Если все элементы меньше барьера, его значение уменьшается, например, на порядок, и снова начинается циклический перебор внедиагональных элементов. Подробнее о методе вращений смотри в [2.1].
Другие алгоритмы решения спектральных задач описаны в специальной литературе [2.1, 2.3, 2.10].
