НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 3: Численное решение систем линейных алгебраических уравнений

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3916 / 1197 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Задачи

Методом Гаусса решить систему линейных уравнений , где
$\mathbf{A} ={\left( \begin{array}{ccc} 5 & 0 & 1 \\ 2 & 6 & {-2}\\ -3 & 2 & 10 \\ \end{array}\right)}, \mathbf{f} = {(11, 8, 6)}^{\mathbf{T}}$

или

$\begin{gather*} 5{x}_1 + 0 \cdot{x}_2 +{x}_3 = 11, \\ 2{x}_1 + 6 \cdot{x}_2 + 2{x}_3 = 8, \\ - 3{x}_1 + 2 \cdot{x}_2 + 10{x}_3 = 6. \end{gather*}$

Решение.Расширенная матрица $\tilde{\mathbf{A}}$ имеет вид

$\tilde{\mathbf{A}} = \left( \begin{array}{cccc} {{a}_{11}} & {{a}_{12}} & {{a}_{13}} & {f}_1 \\ {{a}_{21}} & {{a}_{22}} & {{a}_{23}} & {f}_2 \\ {{a}_{31}} & {{a}_{32}} & {{a}_{33}} & {f_3}\\ \end{array}\right) = \left( \begin{array}{cccc} 5 & 0 & 1 & 11\\ 2 & 6 & {-2} & 8 \\ -3 & 2 & 10 & 6 \\ \end{array}\right)$

Разделив элементы первой строки на ведущий элемент a₁₁= 5 получаем первую опорную строку (1, 0, 0.2, 2.2).

Далее умножим ее на a₂₁= 2 и вычтем из второй строки, после чего умножим опорную строку на a₃₁= 3 и вычтем из третьей. Получаем матрицу $\tilde{\mathbf{A}}_1$

$\tilde{\mathbf{A}} = \left( \begin{array}{cccc} {{a}_{11}} & {{a}_{12}} & {{a}_{13}} & {{f}_1}\\ 0 & {\tilde{a}_{22}} & {\tilde{a}_{23}} & {\tilde{f}_2}\\ 0 & {\tilde{a}_{32}} & {\tilde{a}_{33}} & {\tilde{f}_3}\\ \end{array}\right) = \left( \begin{array}{cccc} 1 & 0 & 0.2 & 2.2\\ 0 & 6 & {-2.4} & 3.6 \\ 0 & 2 & 10.6 & 12.6 \\ \end{array}\right)$

Вторая опорная строка — результат деления второй строки матрицы $\tilde{\mathbf{A}}_1$ на

:
```
(0, 1, - 0.4, 0.6)
```
Матрицы $\tilde{\mathbf{A}}_2$ после умножения опорной строки на 2 и вычитания ее из третьей

$\tilde{\mathbf{A}}= \left( \begin{array}{cccc} {{a}_{11}} & {{a}_{12}} & {{a}_{13}} & {f}_1 \\ 0 & {\tilde{a}_{22}} & {\tilde{a}_{23}} & {\tilde{f}_2}\\ 0 & 0 & {\tilde{\tilde{a}}_{33}} & {\tilde{\tilde{f}}_3}\\ \end{array}\right) = \left( \begin{array}{cccc} 1 & 0 & 0.2 & 2.2\\ 0 & 6 & {-0.4} & 0.6 \\ 0 & 0 & 11.4 & 11.4 \\ \end{array}\right)$

Третья опорная строка (результат деления третьей строки на 11,4 ) есть (0,0,1,1) .

Матрица $\tilde{\mathbf{A}}_3$ будет

$\tilde{\mathbf{A}}_1 = \left( \begin{array}{cccc} 1 & 0 & {0,2} & {2,2}\\ 0 & 1 & {- 0,4} & {0,6}\\ 0 & 0 & 1 & 1 \\ \end{array}}\right).$

Обратный ход метода Гаусса.

Система уравнений с матрицей $\tilde{\mathbf{A}}_3$

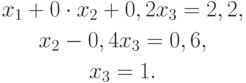
$\begin{gather*} {x}_1 + 0 \cdot{x}_2 + 0,2{x}_3 = 2,2 , \\ {x}_2 - 0,4{x}_3 = 0,6 , \\ {x}_3 = 1. \end{gather*}$

Разрешая эту систему, начиная с последнего уравнения, получим
```
x₃  = 1,  x₂  = 1,  x₁  = 2.
```
Определитель матрицы $\det \mathbf{A}$ можно вычислить как произведение ведущих элементов
Показать, что решение системы линейных уравнений
$\begin{gather*} {x}_1 + 2{x}_2 + 3{x}_3 + 4{x}_4 = 2, \\ {x}_1 + 3{x}_2 + {x}_3 + 2{x}_4 = - 1, \\ 2{x}_1 + 3{x}_2 + 8{x}_3 + 7{x}_4 = 10, \\ 2{x}_1 + 5{x}_2 + 3{x}_3 + 7{x}_4 = 3 \end{gather*}$

методом Гаусса невозможно.

Решение. Преобразование матрицы рассматриваемой системы будет

$\left( \begin{array}{ccccc} 1 & 2 & 3 & 4 & 2 \\ 1 & 3 & 1 & 2 & {- 1}\\ 2 & 3 & 8 & 7 & {10}\\ 2 & 5 & 3 & 7 & 3 \\ \end{array}\right) \to \left( \begin{array}{ccccc} 1 & 2 & 3 & 4 & 2 \\ 0 & 1 & {- 2} & {- 2} & {- 3}\\ 0 & {- 1} & 2 & {- 1} & 6 \\ 0 & 1 & {- 3} & {- 1} & 1 \\ \end{array}\right) \to \left( \begin{array}{ccccc} 1 & 2 & 3 & 4 & 2 \\ 0 & 1 & {- 2} & {- 2} & {- 3}\\ 0 & 0 & 0 & {- 3} & {- 3}\\ 0 & 0 & {- 1} & 1 & 2 \\ \end{array}\right)$

Поскольку ${a^2_{33}} = 0$ то вычисление третьей опорной строки невозможно.
Показать, что
$\mu (\mathbf{A}) \ge \frac{|{\max\limits_i \lambda_i(\mathbf{A})}|}{|{\min\limits_i \lambda_i (\mathbf{A})}|}.$

Рассмотреть случай симметричной матрицы $\mathbf{A}.$

Решение. Для собственного вектора $\omega,$ соответствующего наибольшему по модулю собственному значению матрицы, выполняется равенство $\mathbf{A}\omega = \lambda \omega$ , откуда

$\|{\mathbf{A\omega}}\| = \left|{\max\limits_i\lambda_i}\right|{\|\omega\|}.$
Учитывая, что $\|{\mathbf{A}\omega }\| \le \|\mathbf{A}\|{\|\omega\|}$ , получим $\|\mathbf{A}\| \ge \left|{\max\limits_i \lambda_i (\mathbf{A})}\right|.$ Для обратной матрицы $\mathbf{A}^{-1}$ максимальным по модулю является собственное число $\min\limits_i \lambda_i^{-1}$ , откуда $\left\|{\mathbf{A}^{- 1}}\right\| \ge {\left|{\min\limits_i\lambda_i(\mathbf{A})}\right|}^{- 1}.$ Объединяя два последних неравенства, получим

$\mu (\mathbf{A}) = {\left\|{\mathbf{A}^{- 1}}\right\|}\|\mathbf{A}\| \ge \frac{|{\max\limits_i \lambda_i (\mathbf{A})}|}{|{\min\limits_i \lambda_i (\mathbf{A})}|}.$

В случае симметричной матрицы 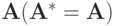$\mathbf{A}(\mathbf{A}^* = \mathbf{A})$ имеем

$\|\mathbf{A}\|}_3 = \sqrt{\lambda_{\max}(\mathbf{A}^*\mathbf{A})} = \sqrt{\lambda_{\max}(\mathbf{A}^2 )}= \sqrt{\lambda_{\max}^2(\mathbf{A})} = |{\lambda_{\max}(\mathbf{A})}|$ ,
т.к. из ${\mathbf{A\omega}}_i = \lambda_i\omega_i$ следует $({\mathbf{A\omega}}_i )^2 = \lambda_i^2\omega_i^2 .$ Аналогично

${\left\|{\mathbf{A}^{- 1}}\right\|}_3 = \sqrt{\lambda_{\max}[(\mathbf{A}^{- 1})^* (\mathbf{A}^{- 1})]} = \sqrt{\lambda_{\max}[(\mathbf{A}^{- 1})]^2} = \\ = \sqrt{\lambda_{\min}^{- 1}(\mathbf{A}^2 )} = |{\lambda_{\min}^{- 1}(\mathbf{A})}|.$
Тогда $\mu (\mathbf{A}) = {\|\mathbf{A}\|}_3{\left\|{\mathbf{A}^{- 1}}\right\|}_3 = |{\lambda_{\max}(\mathbf{A})}|/|{\lambda_{\min}(\mathbf{A})}|.$
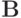Найти число обусловленности матрицы $\mathbf{A}$ , выразив его через число обусловленности матрицы $\mathbf{B}$ , если $\mathbf{A} = {\mathbf{B}}^*{\mathbf{B}} > 0.$
Решение. Для самосопряженной положительной матрицы $\mathbf{A}$ имеем

$\|\mathbf{A}\| = \sup\limits_{\|\mathbf{u}\| \ne 0}\frac{(\mathbf{u}, \mathbf{Au})}{(\mathbf{u}, \mathbf{u})}.$

Тогда

$\mu (\mathbf{A}) = {\|\mathbf{A}\|}_3 \left\|{{\mathbf{A}}^{- 1}}\right\|}_3 = \sup\limits_{\|\mathbf{u}\| \ne 0}\frac{(\mathbf{u, Au})}{(\mathbf{u, u})} \sup\limits_{\|{u}\| \ne 0}\frac{(\mathbf{u}, \mathbf{A}^{- 1}\mathbf{u})}{(\mathbf{u, u})} = \\ = \sup\limits_{\|\mathbf{u}\| \ne 0} \frac{({\mathbf{Bu, Bu}})}{(\mathbf{u,u})}\sup\limits_{\|\mathbf{u}\| \ne 0}\frac{({\mathbf{B}}^{- 1}\mathbf{u},{\mathbf{B}}^{- 1}\mathbf{u})}{(\mathbf{u, u})} = {\|{\mathbf{B}}\|}_3^2 {\left\|{{\mathbf{B}}^{- 1}}\right\|}_3^2,$

откуда

$\mu (\mathbf{A}) = \mu ^2({\mathbf{B}}).$
Показать, что норма матрицы
${\|\mathbf{A}\|}_2 = \max\limits_{1 \le j \le n}\sum\limits_{j= 1}^n{|{a_{ij}}|}$

согласована с нормой вектора

${\|\mathbf{u}\|}_2 = \sum\limits_{i = 1}^n{|{u_i}|}.$
Решение.

${\|\mathbf{Au}\|}_2 = \sum\limits_{i = 1}^n{\left|{\sum\limits_{j= 1}^n{a_{ij}u_j}}\right|} \le \sum\limits_{i = 1}^n{\sum\limits_{j = 1}^n{|{a_{ij}}|}} \cdot |{u_j}| \le \sum\limits_{j = 1}^n{|{u_j}|} \cdot \sum\limits_{i = 1}^n{|{a_{ij}}|} \le \\ \le (\max\limits_{1 \le i \le n}\sum\limits_j{|{a_{ij}}|}) \cdot {\|\mathbf{u}\|}_2 = {\|\mathbf{A}\|}_2 {\|\mathbf{u}\|}_2.$
Положим

$\max \sum\limits_{i = 1}^n{|{a_{ij}}|} = \sum\limits_{i = 1}^n{|{a_{ik}}|}.$
Покажем, что существует вектор $\mathbf{v}$ , для которого достигается равенство. В качестве такового можно взять вектор $\mathbf{v}$ с компонентами ${v}_i = 0, i \ne k, {v}_k = 1.$

Таким образом, норма матрицы ${\|\mathbf{A}\|}_2 = \max\limits_{1 \le j \le n}\sum {|{u_{ij}}|}$ согласована с нормой вектора ${\|\mathbf{u}\|}_2 = \sum\limits_{i = 1}^n{|{u_i}|}.$
Дана жорданова клетка порядка n
$\mathbf{A}= \left( \begin{array}{ccccccc} 1 & {d} & 0 & \ldots & \ldots & 0 & 0 \\ 0 & 1 & {d} & \ldots & \ldots & 0 & 0 \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & \ldots & 1 & {d} & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & \ldots & \ldots & \ldots & 1 & {d}\\ 0 & 0 & \ldots & \ldots & \ldots & \ldots & 1 \\ \end{array} \right).$

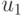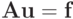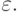
Найти $\mu (\mathbf{A})$ и оценить возмущение в компоненте решения системы $\mathbf{Au} = \mathbf{f}$ , если компонент f_n вектора f возмущен на величину $\varepsilon.$

Решение. Из 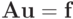$\mathbf{Au}= \mathbf{f}$ следует, что $\mathbf{u}=\mathbf{A}^{- 1}\mathbf{f}.$

С помощью обратной подстановки u_n = 1, u_{n - 1} = ... находим компоненты матрицы

$\mathbf{A}^{- 1}= \left( \begin{array}{ccccccc} 1 & {- d} & {d^2} & \ldots & \ldots & {( - d)^{n - 2}} & {( - d)^{n - 1}}\\ 0 & 1 & {- d} & \ldots & \ldots & {( - d)^{n - 3}} & {( - d)^{n - 2}}\\ 0 & 0 & 1 & \ldots & \ldots & {( - d)^{n - 4}} & {( - d)^{n - 3}}\\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & 0 & \ldots & \ldots & 1 & {- d}\\ 0 & 0 & 0 & \ldots & \ldots & 0 & 1 \\ \end{array} \right).$

В этом случае
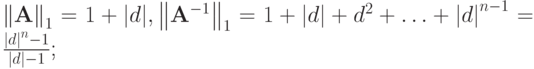
$$ {\|\mathbf{A}\|}_1 = 1 + |{d}|, {\left\|{\mathbf{A}^{- 1}}\right\|}_1 = 1 + |{d}|+{d}^2 + \ldots + {|{d}|}^{n - 1} = \frac{{|{d}|}^n - 1}{|{d}| - 1} $;$

Видно, что при | d | > 1 матрица $\mathbf{A}$ плохо обусловлена, при | d | < 1 - хорошо. При n = 20 и d = 5 имеем $\mu (\mathbf{A}) \approx 10^{14}.$

Компонент $\tilde{u}_1$ решения возмущенной системы $\tilde{\mathbf{u}} = {\mathbf{A}}^{- 1}{\mathbf{\tilde{f}}}$ будет

$\tilde{\mathbf{u}}_1 = f_1 - df_2 + d^2f_3 + \ldots + {(- d)}^{n - 2}f_{n - 1} + {( - d)}^{n - 1}(f_n + \varepsilon ) = u_1 + {(- d)}^{n - 1}\varepsilon,$
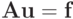
где u₁ — компонент решения невозмущенной системы $\mathbf{Au} = \mathbf{f}$

Отсюда видно, что при | d | > 1 возмущение в n компоненте вектора 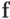$\mathbf{f}$ увеличивается в компоненте u₁ вектора $\mathbf{u}$ в | d |^{n - 1} раз, а при | d | < 1 — в | d |^{n - 1} раз убывает.
Пусть в системе линейных уравнений
```
u₁  + 0,99u₂  = f₁, 
0,99u₁  + u₂  = f₂
```
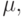вектор $\mathbf{f} = {(f_1, f_2)}^{T}$ получает приращение $\mathbf{\Delta f} = {(\delta f_1, \delta f_2)}^{T}$ , а решение получает приращение $\Delta\mathbf{u} = {(\delta u_1, \delta u_2)}^{T}$ , Найти наименьшее число $\mu,$ при котором независимо от 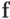$\mathbf{f}$ и $\Delta \mathbf{f}$ выполняется оценка
$\frac{\|{\Delta\mathbf{u}}\|}{\|\mathbf{u}\|} \le \mu \frac{\|{\Delta \mathbf{f}}\|}{\|\mathbf{f}\|}.$

Решить задачу, используя нормы матриц ${\|\cdot\|}_1, {\|\cdot\|}_2 , {\|\cdot\|}_3.$

Решение. Для возмущенной задачи $\mathbf{A}(\mathbf{u} + \Delta\mathbf{u}) = \mathbf{f} + \Delta\mathbf{f}$ , из линейности системы следует $\mathbf{A}\Delta\mathbf{u} = \Delta\mathbf{f}.$ Для возмущения решения выполняется равенство $\Delta\mathbf{u} = {\mathbf{A}}^{- 1}\Delta\mathbf{f}.$ Тогда
$$ \|{\Delta\mathbf{u}}\| \le \|{\mathbf{A}^{- 1}}\| \cdot \|\mathbf{A}\| \cdot \frac{\|{\Delta\mathbf{f}}\|}{\|\mathbf{f}\|} \cdot \frac{\|\mathbf{f}\|}{\|\mathbf{A}\|} $.$

Отсюда сразу следует
$\|{\Delta\mathbf{u}}\| \le \left\|{{\mathbf{A}}^{- 1}}\right\| \cdot \|\mathbf{A}\| \frac{\|{\Delta\mathbf{f}}\|}{\|\mathbf{f}\|}\|\mathbf{u}\|$
, так как
$$ \frac{\|\mathbf{f}\|}{\|\mathbf{A}\|} \le \|{\Delta\mathbf{u}}\| $.$

Тогда искомая оценка будет
$$ \frac{\|{\Delta\mathbf{u}}\|}{\|\mathbf{u}\|} \le \left\|{{\mathbf{A}}^{- 1}}\| \cdot \|\mathbf{A}\| \frac{\|{\Delta\mathbf{f}}\|}{\|\mathbf{f}\|}.$
Обозначим В этом случае наименьшим числом, при котором выполняется оценка
$\frac{\|{\Delta\mathbf{u}}\|}{\|\mathbf{u}\|} \le \mu \frac{\|{\Delta\mathbf{f}}\|}{\|\mathbf{f}\|}$
, является Это — число обусловленности системы уравнений. Численное решение в соответствующих нормах получается легко.
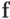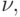При заданном фиксированном $\mathbf{f}$ найти наименьшее число $\nu,$ при котором независимо от 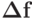$\mathbf{\Delta f}$ выполняется оценка
$$ \frac{\|{\Delta\mathbf{u}}\|}{\|\mathbf{u}\|} \le \nu (f) \frac{\|{\Delta\mathbf{f}}\|}{\|\mathbf{f}\|} $.$

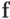Найти такую правую часть системы $\mathbf{f}$ , которой соответствует наименьшее $\nu,$ а также само это значение при использовании третьей нормы матрицы.

Решение.

По условию задачи
$$ \nu \ge \frac{\|\mathbf{f}\|}{\|\mathbf{u}\|} \cdot \frac{\|{\Delta\mathbf{u}}\|}{\|{\Delta\mathbf{f}}\|} $.$
Рассмотрим, какие значения может принимать это число. Точная нижняя грань для такой оценки, очевидно,
$$ \inf\limits_{\|{\Delta\mathbf{f}}\| \ne 0}\nu = \frac{\|\mathbf{f}\|}{\|\mathbf{u}\|} \cdot \sup\limits_{\|{\Delta\mathbf{f}}\| \ne 0} \frac{\left\|{{\mathbf{A}}^{- 1} \cdot \Delta\mathbf{f}}\right\|}{\|{\Delta\mathbf{f}}\|} $.$
Так как надо найти оценку, не зависящую от начального возмущения (при решении конкретной задачи оно, очевидно, неизвестно), получим

$\nu = \inf\limits_{\|{\Delta\mathbf{f}}\| \ne 0}\nu = {\left\|{{\mathbf{A}}^{- 1}}\right\|} \cdot \frac{\|\mathbf{f}\|}{\|\mathbf{u}\|}.$

Для точной нижней грани выполнено
$$ \inf\limits_\mathbf{f}\nu (\mathbf{f}) = \left\|{{\mathbf{A}}^{- 1}}\right\| \times \\ \times {\left({\sup\frac{\|{{\mathbf{A}}^{- 1}\mathbf{f}}\|}{\|\mathbf{f}\|}}\right)}^{- 1} = 1 $.$
Можно оценить и точную верхнюю грань:

$\sup\limits_\mathbf{f}\nu = \left\|{{\mathbf{A}}^{- 1}}\right\| \sup\limits_{\mathbf{u}}\frac{\|\mathbf{Au}\|}{\|\mathbf{u}\|} = \left\|{{\mathbf{A}}^{- 1}}\right\| \cdot \|\mathbf{A}\| = \mu$

Таким образом, $1 \le \nu \le \mu.$

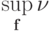Ответим на вопрос, при каких $\mathbf{f}$ достигается $\sup\limits_{\mathbf{f}}\nu$ и $\inf\limits_{\mathbf{f}}\nu.$ Для этого используем разложение вектора правой части системы по базису из собственных векторов матрицы ${\mathbf{A}}^2$ (без ограничения общности полагаем, что такой базис существует). В этом базисе
$\frac{\|\mathbf{Au}\|}{\|\mathbf{u}\|} = \sqrt{\frac{({\mathbf{A}}^*\mathbf{Au, u})}{(\mathbf{u, u})}} - \sqrt{\frac{(\sum{\lambda_i\xi_i\omega_i, \xi_i\omega_i})}{(\xi_i\omega_i, \xi_i\omega_i )}} = \sqrt{\frac{\sum{\lambda_i\xi_i^2}}{\sum{\xi_i^2}}},$

$$ \sqrt{\lambda_{\min}({\mathbf{A}}^*\mathbf{A})} \le \sqrt{\frac{\sum {\lambda_i\xi_i^2}}{\sum{\xi_i^2}}} = \frac{\|\mathbf{Au}\|}{\|\mathbf{u}\|} \le \sqrt{\lambda_{\max}({\mathbf{A}}^*\mathbf{A})} $.$

Для самосопряженной положительной матрицы ${\mathbf{A}}^* = \mathbf{A} > 0$ получаем

$|{\lambda_{\min}(\mathbf{A})}| \le \sqrt{\frac{\sum\limits_i {\lambda_i \xi_i^2}}{\sum\limits_i{\xi_i^2}}} = \frac{\|\mathbf{Au}\|}{\|\mathbf{u}\|} \le |{\lambda_{\max}(\mathbf{A})}|.$

В то же время

$\frac{\|{{\mathbf{A\omega}}_i}\|}{\|{\omega_i}\|} = \sqrt{\frac{(\mathbf{A}*{\mathbf{A\omega}}_i, \omega_i )}{(\omega_i, \omega_i )}} = \sqrt{\frac{\lambda_i (\omega_i, \omega_i )}{(\omega_i ,\omega_i )}} = \sqrt{\lambda_i (\mathbf{A}*\mathbf{A})},$

для самосопряженной положительной матрицы
$$ \frac{\|{{\mathbf{A\omega}}_i}\|}{\|{\omega_i}\|} = |{\lambda_i (\mathbf{A})}| $.$

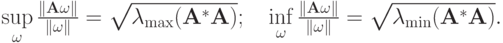
$\sup\limits_\omega\frac{\|{{\mathbf{A\omega}}}\|}{\|\omega\|} = \sqrt{\lambda_{\max}({\mathbf{A}}^*\mathbf{A})};\quad \inf\limits_\omega \frac{\|{{\mathbf{A\omega}}}\|}{\|\omega\|} = \sqrt{\lambda_{\min}({\mathbf{A}}^*\mathbf{A})}.$

В случае 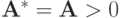${\mathbf{A}}^* = \mathbf{A} > 0$ получаем $\sup\limits_\omega \frac{\|{{\mathbf{A\omega}}}\|}{\|\omega\|} = |{\lambda_{\max}(\mathbf{A})}| \inf\limits_\omega \frac{\|{{\mathbf{A\omega}}}\|}{\|\omega\|} = |{\lambda_{\min}(\mathbf{A})}| $.$

Таким образом,

$\sup\limits_\mathbf{u} \frac{\|\mathbf{Au}\|}{\|\mathbf{u}\|} = \sqrt{\lambda_{\max}({\mathbf{A}}^*\mathbf{A});} \sup\limits_\omega\frac{\|{{\mathbf{A\omega}}}\|}{\|\omega\|} = \sqrt{\lambda_{\max}({\mathbf{A}}^*\mathbf{A})},$

$\inf\limits_\mathbf{u}\frac{\|\mathbf{Au}\|}{\|\mathbf{u}\|} = \sqrt{\lambda_{\min}({\mathbf{A}}^*\mathbf{A});} \inf\limits_\omega \frac{\|{{\mathbf{A\omega}}}\|}{\|\omega\|} = \sqrt{\lambda_{\min}({\mathbf{A}}^*\mathbf{A})}.$
Выписать формулы итерационных методов Якоби, Зейделя, верхней релаксации для СЛАУ
$\mathbf{Ax}= \mathbf{f}, \mathbf{A}= \left( \begin{array}{cc} 2 & 1 \\ 1 & 2 \\ \end{array}\right), \mathbf{x} = {(1,-1)}^{T}, \mathbf{f} = {(1,-1)}^{T}$

или
```
2u + v = 1, 
u + 2v = - 1.
```
Оценить количество итераций для метода Якоби.

(Решение системы: u = 1; v = -1 ).

Решение.

Итерационные методы Якоби, Зейделя, релаксации соответственно записываются

$\left\{ \begin{array}{ccc} u_{k + 1} = - \frac{1}{2}v_k + \frac{1}{2}, \\ v_{k + 1} = - \frac{1}{2}u_k - \frac{1}{2}, \\ \end{array} \right.$
,
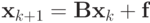или ${\mathbf{x}}_{k+ 1} = {\mathbf{Bx}}_k + \mathbf{f}$ ,

${\mathbf{B}}= \left( \begin{array}{cc} 0 & {- 0,5}\\ {- 0,5} & 0 \\ \end{array} \right),$

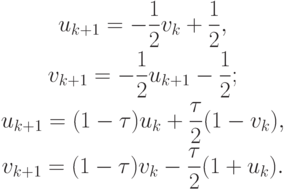
$\begin{gather*} u_{k + 1} = - \frac{1}{2}v_k + \frac{1}{2}, \\ v_{k + 1} = - \frac{1}{2}u_{k + 1} - \frac{1}{2}; \\ u_{k + 1} = (1 - \tau )u_k + \frac{\tau}{2}(1 - v_k), \\ v_{k + 1} = (1 - \tau )v_k - \frac{\tau}{2}(1 + u_k). \end{gather*}$

Оценка количества итераций проводится по формуле

$k \approx \ln \frac{\varepsilon }{\varepsilon_0 }/\ln \|\mathbf{B}\| = \ln 10^{- 3}/\ln \frac{1}{2}.$
Представить графическую интерпретацию итерационного метода Якоби для СЛАУ
$\begin{gather*} a_{11}u + a_{12}v = f_1, \\ a_{21}u + a_{22}v= f_2, \\ a_{11} \ne 0, a_{22} \ne 0 \end{gather*}$

Решение. Итерационный процесс Якоби записывается как

$\begin{gather*}u_{k+ 1} = - \frac{a_{12}}{a_{11}}v_k + \frac{f_1}{a_{11}}, \\ v_{k+ 1} = - \frac{a_{21}}{a_{22}}u_k + \frac{f_2}{a_{22}}. \end{gather*}$

Рис. 2.1.

Первое уравнение соответствует прямой 1, второе — прямой 2. Вычисление u₁ соответствует проведению отрезка, параллельного оси 0u и (при v = v₀ ) до пересечения с прямой 1 ; точка пересечения даст первое приближение u₁. Вычислению v₁ соответствует проведение из точки A₁ прямой, параллельной оси 0v до пересечения с прямой 2 и т.д. до сходимости итераций к точке пересечения прямых 1 и 2 (A_k) с заданной точностью.
При каких a,b сходится метод простой итерации ${\mathbf{u}}_{k+ 1} = {\mathbf{Bu}}_k + \mathbf{f}$ , где
${\mathbf{B}} = \left( \begin{array}{ccc} {a} & {b} & 0 \\ {b} & {a} & {b}\\ 0 & {b} & {a} \\ \end{array} \right).$

Решение. Для того, чтобы метод простой итерации сходился к решению соответствующей СЛАУ, необходимо и достаточно, чтобы все собственные значения матрицы 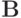$\mathbf{B}$ по модулю были меньше единицы: $|\lambda _{i}| < 1.$ Решаем характеристическое уравнение

$\begin{gather*} det (\mathbf{B}- \lambda \mathbf{E}) = {\left| \begin{array}{ccc} {a - \lambda } & {b} & 0 \\ {b} & {{a}-{\lambda}} & {b}\\ 0 & {b} & {{a}-{\lambda}}\\ \end{array} \right|} = \\ = (a - \lambda ) {\left| \begin{array}{cc} {{a}-{\lambda}} & {b}\\ {b} & {{a}-{\lambda}}\\ \end{array} \right|} - b{\left| \begin{array}{cc} {b} & {a}\\ 0 & {{a}-{\lambda}}\\ \end{array} \right|} = \\ = (a - \lambda )\left[{{(a - \lambda )}^2 - b^2}\right] - b^2 (a - \lambda ) = \\ = (a - \lambda )(a - \lambda - \sqrt{2b})(a - \lambda + \sqrt{2b}) = 0, \end{gather*}$

откуда получим условие сходимости итерационного метода

$|{a}| < 1, |{a \pm \sqrt{2b}}| < 1.$
Найти условие сходимости итерационных методов Якоби и Зейделя для СЛАУ 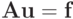$\mathbf{Au} = \mathbf{f}$ с матрицей
$\mathbf{A}$ вида
$\mathbf{A} = \left( \begin{array}{ccc} {a} & {b} & 0 \\ {b} & {a} & {b}\\ 0 & {b} & {a}\\ \end{array} \right).$

Решение. Для метода Якоби

${\mathbf{u}}_{k + 1} = {\mathbf{Bu}}_k + \mathbf{f},\quad \mbox{где}\quad {\mathbf{B}} = -{\mathbf{D}}^{- 1}({\mathbf{L}} + {\mathbf{U}}).$
Имеет место уравнение:

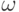${\mathbf{B\omega}} = \lambda \omega$ , где $\lambda$ и $\mathbf{\omega}$ — собственное число и собственный вектор, соответственно. В таком случае $- {\mathbf{D}}({\mathbf{L}} + {\mathbf{U}})\omega = \lambda\omega$ , или: $({\mathbf{L}} + {\mathbf{U}} + \lambda{\mathbf{D}}) \omega = 0$ , откуда (предполагаем наличие нетривиальных решений у последней СЛАУ ):

$\det ({\mathbf{L}} + {\mathbf{U}} + \lambda{\mathbf{D}}) = 0.$
Решим это уравнение:

$\det {\left| \begin{array}{ccc} \lambda a & b & 0\\ b & \lambda a & b\\ 0 & b & \lambda a \end{array} \right|} = 0,$

откуда получим условия сходимости итерационного метода Якоби:

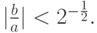
$|{\frac{b}{a}}| < 2^{- \frac{1}{2}}.$

Для метода Зейделя имеем

${\mathbf{B}} = {- (\mathbf{D} + \mathbf{L})}^{- 1}{\mathbf{U}},\quad {\mathbf{B\omega}} = \lambda\omega.$
В таком случае

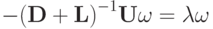${- (\mathbf{D} + \mathbf{L})}^{- 1}{\mathbf{U\omega}} = \lambda\omega$ ,
откуда следует уравнение

$\det (\lambda{\mathbf{L}} + \lambda {\mathbf{D}} + {\mathbf{U}}) = 0$ ,
Вычислив детерминант, придем к алгебраическому уравнению

$\det {\left( \begin{array}{ccc} \lambda a & b & 0 \\ \lambda b & \lambda a & b \\ 0 & \lambda b & \lambda a \end{array} \right) } = a{\lambda}^2(a^2\lambda - 2b^2) = 0.$

В таком случае, поскольку
$\lambda_{1,2}= 0, \lambda_3 = 2\frac{b^2}{a^2}$
, получим условие сходимости метода Зейделя:
$$ \frac{b}{a} < 2^{- \frac{1}{2}}$.$
Видно, что в данном случае условия сходимости для обоих методов совпадают.