Численное решение систем линейных алгебраических уравнений
2.4. Прямые методы решения СЛАУ
Трудность численного решения рассматриваемых СЛАУ определяется видом
матрицы  Легко получается решение системы с диагональной матрицей, в этом случае система распадается на n линейных уравнений, каждое из которых содержит лишь одну неизвестную величину. Для диагональной системы очевидны явные формулы
Легко получается решение системы с диагональной матрицей, в этом случае система распадается на n линейных уравнений, каждое из которых содержит лишь одну неизвестную величину. Для диагональной системы очевидны явные формулы
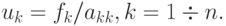
В случае треугольной матрицы
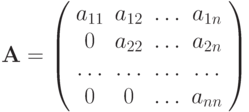
из последнего уравнения получаем 
Решая систему линейных уравнений с треугольной матрицей "снизу вверх", для uk имеем
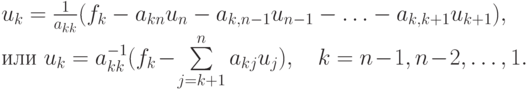
Можно оценить количество арифметических действий, затрачиваемых на решение такой системы. Оно составляет O(n2) .
Пусть теперь система уравнений имеет матрицу общего вида. Стандартная схема такого решения разделяется на два этапа: прямой ход — приведение матрицы к треугольному виду, и обратный — вычисление решения системы.
2.4.1. Метод исключения Гаусса
Рассматривается система уравнений
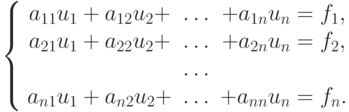 |
( 2.10) |
Прямой ход метода Гаусса состоит в следующем. Положим, что 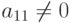 и исключим u1 из всех уравнений, начиная со второго,
для чего ко второму уравнению прибавим первое, умноженное на
и исключим u1 из всех уравнений, начиная со второго,
для чего ко второму уравнению прибавим первое, умноженное на 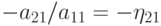 , к третьему прибавим первое, умноженное на
, к третьему прибавим первое, умноженное на 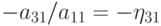 и т.д. После этих преобразований получим эквивалентную систему:
и т.д. После этих преобразований получим эквивалентную систему:
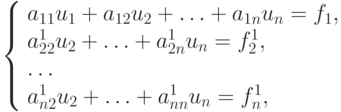 |
( 2.11) |
в которой коэффициенты и правые части определяются следующим образом:
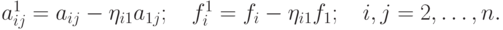
Теперь положим 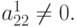 Аналогично, вычислив множители второго шага
Аналогично, вычислив множители второго шага 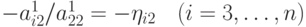 ,
исключаем u2 из последних (n - 2) уравнений системы (2.17). В результате преобразований получим новую эквивалентную систему уравнений
,
исключаем u2 из последних (n - 2) уравнений системы (2.17). В результате преобразований получим новую эквивалентную систему уравнений
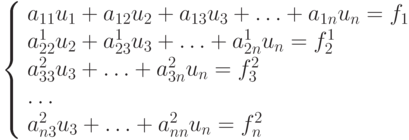
в которой 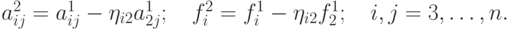 Продолжая алгоритм, т.е. исключая ui (i = k + 1, ..., n), приходим на n - 1 шаге к системе с треугольной матрицей
Продолжая алгоритм, т.е. исключая ui (i = k + 1, ..., n), приходим на n - 1 шаге к системе с треугольной матрицей
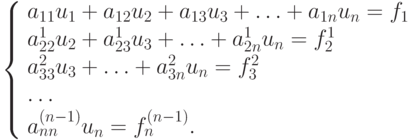 |
( 2.12) |
Обратный ход метода Гаусса позволяет определить решение системы линейных уравнений. Из последнего уравнения системы находим un ; подставляем это значение в предпоследнее уравнение, получим un-1. Поступая так и далее, последовательно находим un-2, un-3, ..., u1. Вычисления компонент вектора решения проводятся по формулам
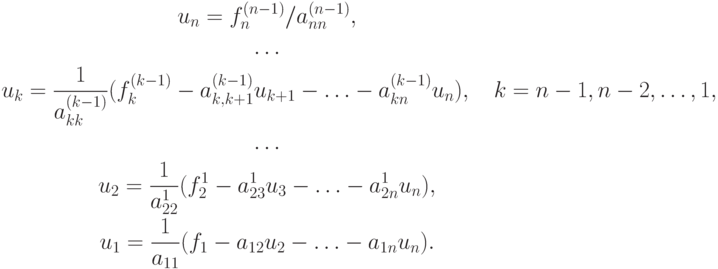
Этот алгоритм прост и легко реализуем при условии, что 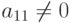 ,
, 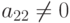 и т.д. Количество арифметических действий прямого хода
и т.д. Количество арифметических действий прямого хода 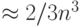 , обратного
, обратного 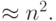 Это уже приемлемая для современных компьютеров величина.
Это уже приемлемая для современных компьютеров величина.
Рассмотрим метод Гаусса с позиции операций с матрицами. Пусть  — матрица системы после исключения первого неизвестного
— матрица системы после исключения первого неизвестного
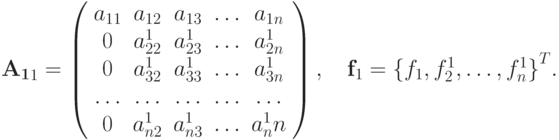
Введем новую матрицу
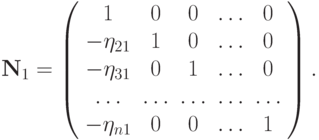
Очевидно, 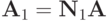 ,
,  Аналогично, после второго шага система приводится к виду
Аналогично, после второго шага система приводится к виду 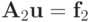 , где
, где  ,
, 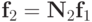 ,
,
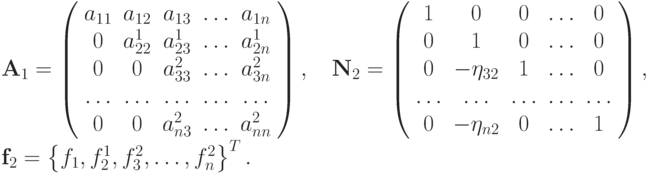
После n - 1 шага получим 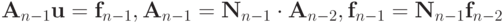 ,
,
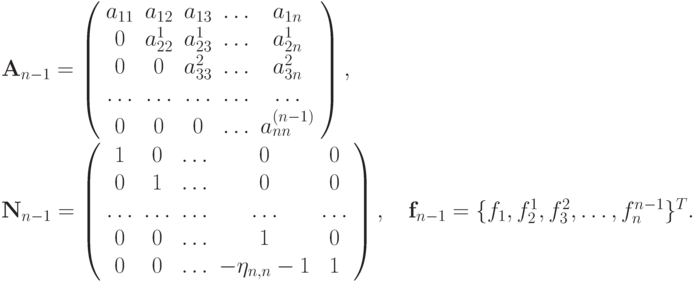
В итоге получаются матрица и вектор 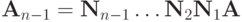 ,
,  , откуда
, откуда 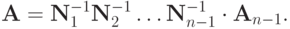 При этом
При этом
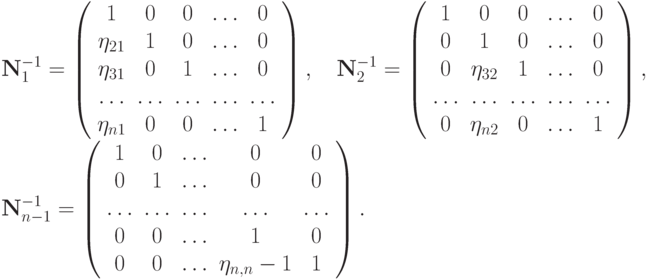
После введения обозначений  ,
,  , где
, где
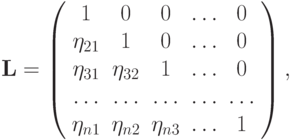
получим 
Это представление матрицы  называется LU-разложением (на произведение нижней и верхней треугольных матриц
называется LU-разложением (на произведение нижней и верхней треугольных матриц 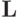 и
и  ). Прямой ход метода Гаусса можно рассматривать как один из вариантов представления матрицы в виде произведения двух треугольных матриц, или LU-разложения. Его можно провести и другими способами.
). Прямой ход метода Гаусса можно рассматривать как один из вариантов представления матрицы в виде произведения двух треугольных матриц, или LU-разложения. Его можно провести и другими способами.
Вспомним "отрицательный" пример из "Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования" . Пусть необходимо решить систему
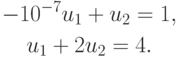
Исключая u1 из первого уравнения и подставляя во второе, получим u2 = (107 + 4)/(107 + 2). После вычислений с семью значащими цифрами получаем u1 = 0,000000, u2 = 1,000000, что неверно (см. второе уравнение). Теперь исключим u1 из второго уравнения и подставим в первое. При этом получим
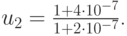
В реальных вычислениях используются методы с выбором главного (или ведущего ) элемента. Выбор главного элемента по столбцам реализуется следующим образом: перед исключением u1 отыскивается 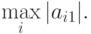 Пусть максимум достигается при i = k. В этом случае меняются местами первое и k уравнения (или в матрице меняются местами две строки) и реализуется процедура исключения.
Пусть максимум достигается при i = k. В этом случае меняются местами первое и k уравнения (или в матрице меняются местами две строки) и реализуется процедура исключения.
Затем отыскивается 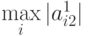 , и процедура поиска главного элемента в столбцах повторяется. Так же реализуется выбор главного элемента
по строкам: перед исключением u1 отыскивается
, и процедура поиска главного элемента в столбцах повторяется. Так же реализуется выбор главного элемента
по строкам: перед исключением u1 отыскивается 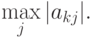 Если максимум достигается при i = k, то у u1 и uk меняются номера, то есть максимальный элемент из коэффициентов первого уравнения окажется на месте a11, и т.д. Наиболее эффективным является метод Гаусса с выбором главного элемента по всей матрице. Во многих методах важным является условие диагонального преобладания
Если максимум достигается при i = k, то у u1 и uk меняются номера, то есть максимальный элемент из коэффициентов первого уравнения окажется на месте a11, и т.д. Наиболее эффективным является метод Гаусса с выбором главного элемента по всей матрице. Во многих методах важным является условие диагонального преобладания
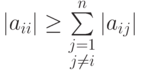
Полученное решение можно улучшить следующим образом. Пусть 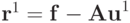 есть невязка, допущенная при решении рассматриваемой системы (
есть невязка, допущенная при решении рассматриваемой системы ( 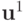 — полученное численное решение) за счет ошибки округлений. Очевидно, что погрешность
— полученное численное решение) за счет ошибки округлений. Очевидно, что погрешность 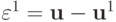 удовлетворяет СЛАУ
удовлетворяет СЛАУ 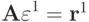 , так как
, так как 
Решив последнюю систему, получаем 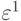 ,
после чего уточняем решение:
,
после чего уточняем решение:
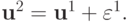
Эту процедуру можно продолжить.
