НОУ ИНТУИТ | Структуры данных и модели вычислений. Лекция 9: Толстые кучи

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 26.09.2006 | Доступ: свободный | Студентов: 1800 / 485 | Оценка: 4.25 / 4.12 | Длительность: 17:09:00

ISBN: 978-5-9556-0066-6

Тема: Алгоритмы и дискретные структуры

Специальности: Программист, Математик

|

Вам нравится? Нравится 19 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Толстая куча

Толстая куча — это почти кучеобразный нагруженный лес.

Представление толстой кучи. Каждый узел толстой кучи будем представлять записью следующего вида:

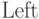$\eq*{ {\rm FatNode} = ({\rm Key}, {\rm Parent}, {\rm Left}, {\rm Right}, {\rm LChild}, {\rm Rank}), }$

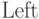где ${\rm Key}$ — ключ элемента, приписанного узлу дерева; ${\rm Parent}$ — указатель на родителя; ${\rm Left}$ — указатель на ближайшего левого брата; ${\rm Right}$ — указатель на ближайшего правого брата; ${\rm LChild}$ — указатель на самого левого сына; ${\rm Rank}$ — ранг узла. Таким образом, "братья" связаны в двусвязный список при помощи указателей ${\rm Left}$ и ${\rm Right}$ . У самого левого (правого) "брата" в этом списке указатель ${\rm Left}$ ( ${\rm Right}$ ) заземлен.

На рис. 9.2 представлено толстое дерево 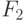F_2 (внутри узлов указаны их ранги).

Рис. 9.2.

Вспомогательные структуры

Для представления толстой кучи введем новую структуру, которую назовем корневым счетчиком, а для того, чтобы быстро находить неправильные узлы, введем еще один избыточный счетчик, который назовем счетчиком нарушений. Таким образом, толстую кучу можно представить записью следующего вида:

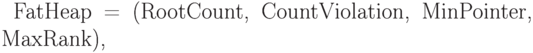
$\eq*{ {\rm FatHeap} = ({\rm RootCount}, {\rm CountViolation}, {\rm MinPointer}, {\rm MaxRank}), }$

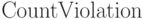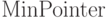где ${\rm RootCount}$ — массив, соответствующий корневому счетчику; ${\rm CountViolation}$ — массив, соответствующий счетчику нарушений; ${\rm MinPointer}$ — указатель на элемент кучи, имеющий минимальный ключ; ${\rm MaxRank}$ — наибольший ранг среди рангов деревьев, присутствующих в куче.

Корневой счетчик. Корневой счетчик состоит из избыточного троичного представления числа элементов в куче и набора списочных элементов.

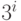Значение -го разряда избыточного корневого представления равно количеству деревьев ранга , присутствующих в куче. При таком определении избыточного корневого представления число, которое оно представляет, равно числу узлов в куче, так как толстое дерево ранга содержит ровно 3^i узлов. Заметим, что состояние избыточного корневого представления определяется неоднозначно. Отсюда следует, что толстая куча с одним и тем же набором элементов может быть представлена различными наборами толстых деревьев. Очевидно, что для любой толстой кучи, состоящей из элементов, существует регулярное избыточное представление корневого счетчика.

Списочный элемент, приписанный -му разряду избыточного корневого представления, — это указатель на список деревьев ранга , присутствующих в куче, образованный посредством указателей ${\rm Right}$ корневых узлов связываемых деревьев.

Определение корневого счетчика дает возможность сделать несколько утверждений:

Корневой счетчик позволяет иметь доступ к корню любого дерева ранга за время .
Вставка толстого дерева ранга соответствует операции инкрементирования -го разряда корневого счетчика.
Удаление толстого поддерева ранга соответствует операции декрементирования -го разряда корневого счетчика.
Операции инкрементирования и декрементирования -го разряда корневого счетчика осуществляются за время .

Представление корневого счетчика. Корневой счетчик представляем расширяющимся массивом ${\rm RootCount}$ , каждый элемент которого — запись с тремя полями:

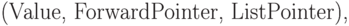
$\eq*{ ({\rm Value}, {\rm ForwardPointer}, {\rm ListPointer}), }$

которые интерпретируем следующим образом:

${\rm RootCount}[i].{\rm Value}$ — -й разряд, равный количеству деревьев ранга ;
${\rm RootCount}[i].{\rm ForwardPointer}$ — прямой указатель -го разряда;
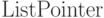${\rm RootCount}[i].{\rm ListPointer}$ — указатель на список деревьев ранга , присутствующих в толстой куче. Деревья в этом списке связаны при помощи указателя ${\rm Right}$ корневых узлов связываемых деревьев. Если в куче нет деревьев ранга , то указатель ${\rm ListPointer}$ заземлен. Заметим, что если значение ${\rm RootCount}[i].{\rm Value}$ равно нулю, то нам неважно, каково значение указателя ${\rm RootCount}[i].{\rm ListPointer}$ .

Инициализация корневого счетчика (InitRootCount). Поскольку корневой счетчик реализован как массив записей, возникает вопрос о величине данного массива и о том, что делать, когда весь этот массив заполнен. Чтобы была возможность оценить время инициализации счетчиков величиной O(1) , используем поразрядную их инициализацию. То есть будем добавлять новые разряды только тогда, когда возникает такая необходимость, и при этом инициализировать новый разряд сразу в обоих счетчиках. Для этого мы вводим переменную ${\rm MaxRank}$ , которая показывает нам, какая часть массивов счетчиков используется в данный момент.

При начальной инициализации необходимо установить счетчики в состояние, которое отвечает пустой куче. Очевидно, что в пустой куче не может быть никаких нарушений. Операция инициализации выглядит следующим образом.

Обновление прямого указателя i-го разряда корневого счетчика ${\rm UpdateForwardPointer(i)$ заключается в выполнении операторов

$\formula{ \t If\ ({\rm RootCount}[i+1].{\rm Value} = 3-1)\\ \mbox{}\q \t then\ {\rm RootCount}[i].{\rm ForwardPointer} := {\rm RootCount}[i+1].{\rm ForwardPointer}\\ \mbox{}\q \t else\ \t{RootCount}[i].\t{ForwardPointer}:= i+1; }$

Корректировка списочной части i-го разряда корневого счетчика при вставке в кучу нового дерева ранга i $({\rm InsertTree(i,p)})$ . Эта процедура вставляет новое дерево ранга (на него указывает указатель ) в списочную часть -го разряда корневого счетчика ${\rm RootCount}$ и заключается в выполнении операторов

$\formula{ p1 := {\rm RootCount}[i].{\rm ListPointer};\\ \t if\ ({\rm RootCount}[i].{\rm Value} \ne 0)\ \t then\ p\t{\^{}.}{\rm Right} := p1\ \t {else}\ p\t{\^{}}.{\rm Right} := {\rm nil};\\ p\t{\^{}.}{\rm Left}:= {\rm nil}; {\rm RootCount}[i].{\rm ListPointer} := p; }$

Корректировка списочной части i>-го разряда корневого счетчика при удалении из кучи дерева ранга i $({\rm DeleteTree (i; p))$ . Эта процедура удаляет дерево ранга (на него указывает указатель ) из списочной части -го разряда корневого счетчика ${\rm RootCount}$ . Будем считать, что указанное дерево присутствует в куче. Процедура заключается в выполнении операторов

$\formula{ p1:= {\rm RootCount}[i].{\rm ListPointer};\\ \t If\ (p1 = p)\ \t then\ {\rm RootCount}[i].{\rm ListPointer} := p\t{\^{}}.{\rm Right};\\ j:= 1;\\ \t while\ (j \le {\rm RootCount}[i].{\rm Value})\ \t{and}\ (p1\t{\^{}}.{\rm Right} \ne p)\ \t do\\ \t begin\ j:= j+1;\ p1 := p1\t{\^{}.}{\rm Right}\,{\rm End}; \\ p1\t{\^{}.}{\rm Right} := p\t{\^{}}.{\rm Right}; }$

Связывание (Fastening (p1, p2, p3)) трех толстых деревьев ранга i в одно толстое дерево ранга i +1. Эта функция принимает три указателя 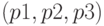на три разных толстых дерева одного и того же ранга и возвращает указатель на вновь сформированное дерево ранга i + 1 .

Дальше >>

Авторизоваться

Структуры данных и модели вычислений

Толстые кучи

Толстая куча

Вспомогательные структуры

Вопросы и ответы