|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Вводная
Амортизационный анализ работы двоичного счетчика
Рассмотрим работу  -разрядного двоичного сбрасываемого
счетчика,
реализованного как массив битов
-разрядного двоичного сбрасываемого
счетчика,
реализованного как массив битов ![A[0 \ldots k-1]](/sites/default/files/tex_cache/76dca2a66ae24f829163d951250a250c.png) , хранящего двоичную
запись числа
, хранящего двоичную
запись числа  . Будем считать, что
. Будем считать, что ![A[0]](/sites/default/files/tex_cache/dedca2c1f57101b400f1f2d5933f8289.png) —
младший разряд.
Пусть первоначально
—
младший разряд.
Пусть первоначально 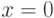 . Единственной операцией в нашем примере
будет операция Increment,
увеличивающая
. Единственной операцией в нашем примере
будет операция Increment,
увеличивающая  на 1
по модулю
на 1
по модулю 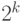 .
.
Увеличение счетчика на единицу происходит следующим образом: все начальные
единичные биты в массиве  , если они есть, становятся нулями,
а следующий непосредственно за ними нулевой бит, если он есть,
устанавливается в единицу. Стоимость операции Increment линейно
зависит от общего количества битов, подвергшихся изменению. Каждое такое
изменение будем считать элементарной операцией.
, если они есть, становятся нулями,
а следующий непосредственно за ними нулевой бит, если он есть,
устанавливается в единицу. Стоимость операции Increment линейно
зависит от общего количества битов, подвергшихся изменению. Каждое такое
изменение будем считать элементарной операцией.
Анализ работы двоичного счетчика
методом группировки.
Применим метод группировки для анализа сложности  -кратного
выполнения операции Increment.
Поскольку в худшем случае, когда
массив
-кратного
выполнения операции Increment.
Поскольку в худшем случае, когда
массив  состоит из одних единиц, меняются все
состоит из одних единиц, меняются все  битов, то
битов, то  -кратное выполнение операции Increment может быть оценено
как
-кратное выполнение операции Increment может быть оценено
как 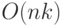 элементарных операций. Но эта оценка слишком груба.
элементарных операций. Но эта оценка слишком груба.
Чтобы получить более точную оценку, учтем, что не каждый раз значения
всех  битов меняются. В самом деле, младший бит
битов меняются. В самом деле, младший бит ![A[0]](/sites/default/files/tex_cache/dedca2c1f57101b400f1f2d5933f8289.png) меняется при
каждом исполнении операции Increment. Следующий по старшинству бит
меняется при
каждом исполнении операции Increment. Следующий по старшинству бит ![A[1]](/sites/default/files/tex_cache/4c91b246bb2d1dadc430ab7ac1affa99.png) меняется только через раз. При счете от нуля
до
меняется только через раз. При счете от нуля
до  этот
бит меняется
этот
бит меняется ![[n/2]](/sites/default/files/tex_cache/1df61e7f2446684a7a300e9420d62011.png) раз. Бит
раз. Бит ![A[2]](/sites/default/files/tex_cache/5a242e1b94e0ccb2f9eecf192b7a2b12.png) меняется только
каждый четвертый раз, и так далее. Заметим, что если
меняется только
каждый четвертый раз, и так далее. Заметим, что если 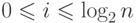 , то в процессе счета от
, то в процессе счета от  до
до  разряд
разряд ![A[i]](/sites/default/files/tex_cache/8a6b5ab46e06fa60418f7c34e624b076.png) меняется
меняется ![[n/2^i]](/sites/default/files/tex_cache/e11dd8191aabb4b1a677237725893844.png) раз, а если
раз, а если ![i
> [\log_2 n]](/sites/default/files/tex_cache/9d143896323a3ac862b918b303959301.png) , то он вообще не меняется. Следовательно, общее количество
операций зануления и записи 1 равно
, то он вообще не меняется. Следовательно, общее количество
операций зануления и записи 1 равно
![\eq*{
n + [n/2] + [n/4] + \ldots + [n/2]^{[\log n]} < n(1 + 1/2 + 1/4 + \ldots)
= 2n.
}](/sites/default/files/tex_cache/fe12f4e8403a5692c02412bf6254548e.png)
 до
до  требует не более
требует не более  операций, причем константа не зависит
от
операций, причем константа не зависит
от  и равна
и равна  . Учетную стоимость операции Increment можно считать
равной
. Учетную стоимость операции Increment можно считать
равной 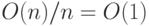 .
.Анализ работы двоичного счетчика
методом предоплаты.
Применим метод предоплаты для анализа сложности  -кратного
выполнения операции Increment.
Будем считать, что реальная стоимость
изменения бита составляет
-кратного
выполнения операции Increment.
Будем считать, что реальная стоимость
изменения бита составляет  рубль. Установим такие учетные
стоимости:
рубль. Установим такие учетные
стоимости:  рубля за запись единицы,
рубля за запись единицы,  за очистку.
При каждой установке бита в единицу
одним из двух рублей учетной стоимости будем расплачиваться за реальные
затраты на эту установку, а второй рубль, остающийся в резерве, будем
"прикреплять" к рассматриваемому биту. Поскольку первоначально все
биты были нулевыми, в каждый момент к каждому ненулевому биту будет прикреплен
резервный рубль. Стало быть, за очистку любого бита дополнительно платить
нам не придется: мы расплатимся за нее рублем, прикрепленным к этому биту
в момент его установки.
за очистку.
При каждой установке бита в единицу
одним из двух рублей учетной стоимости будем расплачиваться за реальные
затраты на эту установку, а второй рубль, остающийся в резерве, будем
"прикреплять" к рассматриваемому биту. Поскольку первоначально все
биты были нулевыми, в каждый момент к каждому ненулевому биту будет прикреплен
резервный рубль. Стало быть, за очистку любого бита дополнительно платить
нам не придется: мы расплатимся за нее рублем, прикрепленным к этому биту
в момент его установки.
Теперь легко определить учетную стоимость операции Increment.
Поскольку каждая такая операция требует не более одной установки бита, ее
учетную стоимость можно считать равной  рублям. Следовательно,
фактическая стоимость
рублям. Следовательно,
фактическая стоимость  последовательных операций Increment,
начинающихся с нуля, есть
последовательных операций Increment,
начинающихся с нуля, есть  , поскольку она не превосходит
суммы учетных стоимостей
, поскольку она не превосходит
суммы учетных стоимостей  .
.
Анализ работы двоичного счетчика
методом потенциалов.
Проанализируем теперь трудоемкость  -кратного выполнения операции Increment с помощью метода
потенциалов.
-кратного выполнения операции Increment с помощью метода
потенциалов.
Пусть 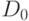 — содержимое счетчика в начальный
момент,
— содержимое счетчика в начальный
момент, 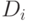 —
содержимое счетчика после выполнения
—
содержимое счетчика после выполнения  -й операции,
-й операции, 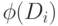 — число единиц
в записи
— число единиц
в записи 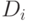 ,
, 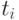 — число единиц,
превращенных в нули при
— число единиц,
превращенных в нули при  -й операции. Очевидно, что
-й операции. Очевидно, что

Пусть далее  — реальная стоимость
— реальная стоимость  -й
операции Increment,
-й
операции Increment, 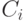 — ее учетная стоимость. Очевидно, что
— ее учетная стоимость. Очевидно, что 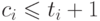 . Тогда
. Тогда
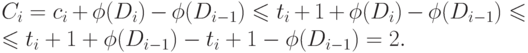
Если счет начинается с нуля, то

и
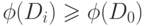
для всех  . Поскольку сумма учетных стоимостей оценивает сверху
сумму реальных стоимостей, имеем
. Поскольку сумма учетных стоимостей оценивает сверху
сумму реальных стоимостей, имеем
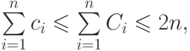
то есть получаем, что суммарная стоимость  операций есть
операций есть  с константой (двойкой), не зависящей от
с константой (двойкой), не зависящей от  .
.
Метод потенциалов позволяет разобраться и со случаем, когда счет начинается не с нуля. В этом случае имеем

откуда при достаточно больших значениях  (
(  )
получаем, что реальная стоимость оценивается как
)
получаем, что реальная стоимость оценивается как  , причем
константа в
, причем
константа в  -записи не зависит ни от
-записи не зависит ни от  , ни от
начального
значения счетчика.
, ни от
начального
значения счетчика.
