|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Вводная
Классы функций, используемые для оценки сложности алгоритмов
Все функции, используемые ниже для оценки сложности алгоритмов, считаются
асимптотически неотрицательными функциями натурального аргумента, то есть
неотрицательными, начиная с некоторого значения аргумента  .
.
Для асимптотических оценок сверху используется класс функций
![{
O (g(n))=\{f(n):\exists c>0, \exists n_{0} \forall n>n_{0}
[0\le f(n)\le c\cdot g(n)]\}.
}](/sites/default/files/tex_cache/ad65e2016f5b059de05c10065acfba0c.png)
Для асимптотических оценок снизу используется класс функций
![{
\Omega (g(n))=\{ f(n):\exists c>0,\exists n_{0}
\forall n>n_{0} [0\le c\cdot g(n)\le f(n)]\}.
}](/sites/default/files/tex_cache/33d6be26c61d9054e4e889f42e7b5c06.png)
Для асимптотически точных оценок используется класс функций
![{
\Theta (g(n))=\{ f(n):\exists c_{1},c_{2} >0,\exists n_{0}
\forall n>n_{0} [0\le c_{1} g(n)\le f(n)\le c_{2} g(n)]\}.
}](/sites/default/files/tex_cache/0355a0679c8e445d857cff246973bf0e.png)
Очевидно, что справедливы следующие соотношения
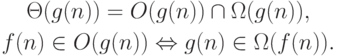
Далее, предполагается знание стандартных функций, используемых при оценках сложности, таких как полиномы, экспоненты, суперэкспоненты, логарифмы, суперлогарифмы, факториалы, числа Фибоначчи. Предполагается умение сравнивать их по скоростям роста.
Амортизационный анализ
Наряду с получением верхних и нижних оценок и оценок в среднем, часто используются так называемые амортизационные оценки.
Амортизационный анализ применяется при оценке времени выполнения
корректной последовательности, состоящей из  однотипных или
разнотипных операций с некоторой структурой данных. Если верхнюю оценку
времени выполнения одной операции умножить на
однотипных или
разнотипных операций с некоторой структурой данных. Если верхнюю оценку
времени выполнения одной операции умножить на  , получим верхнюю
оценку выполнения всех
, получим верхнюю
оценку выполнения всех  операций. Часто такая оценка бывает
сильно
завышенной. Иногда длительное время выполнения очередной операции влечет
за собой малое время выполнения следующих операций. Более того, такая
ситуация может создаваться искусственно, то есть при выполнении очередной
операции мы можем готовить почву для более эффективного выполнения
следующей. Поэтому возникает задача изучения асимптотического поведения
гарантированной оценки для среднего времени выполнения одной операции.
операций. Часто такая оценка бывает
сильно
завышенной. Иногда длительное время выполнения очередной операции влечет
за собой малое время выполнения следующих операций. Более того, такая
ситуация может создаваться искусственно, то есть при выполнении очередной
операции мы можем готовить почву для более эффективного выполнения
следующей. Поэтому возникает задача изучения асимптотического поведения
гарантированной оценки для среднего времени выполнения одной операции.
При амортизационном анализе определяется некоторая так называемая учетная
(амортизационная) стоимость одной операции, которая может быть как больше,
так и меньше реальной стоимости конкретной операции. Но при этом для любой
корректной последовательности операций фактическая суммарная длительность
всех операций не должна превосходить суммы их учетных стоимостей. Зная
учетную стоимость одной операции, верхнюю оценку времени выполнения
последовательности из  операций можно получить, умножив ее
на
операций можно получить, умножив ее
на  .
.
Ниже рассмотрим три часто используемых метода амортизационного анализа: метод группировки, метод предоплаты и метод потенциалов.
Метод группировки. Предположим, что мы оценили сверху время
выполнения последовательности из  операций, установив, что она не
превосходит
операций, установив, что она не
превосходит 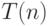 , тогда величину
, тогда величину 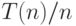 объявим учетной стоимостью любой операции из рассматриваемой
последовательности, независимо от ее длительности.
объявим учетной стоимостью любой операции из рассматриваемой
последовательности, независимо от ее длительности.
Метод предоплаты. В этом методе операции разных типов получают разные учетные стоимости, причем эти стоимости могут быть как больше, так и меньше фактических. Если учетная стоимость превосходит фактическую, то разность между ними рассматривается как резерв на оплату в будущем тех операций, у которых учетная стоимость ниже реальной. Учетные стоимости должны выбираться так, чтобы в любой момент времени фактическая стоимость не превосходила суммы учетных стоимостей, то есть чтобы резерв оставался неотрицательным.
Метод потенциалов. Этот метод является обобщением метода предоплаты. Здесь резерв определяется функцией состояния структуры данных в целом. Эта функция называется потенциалом.
Общая схема метода такова. Пусть над структурой данных предстоит
произвести  операций, и пусть
операций, и пусть 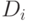 — состояние
структуры данных после
— состояние
структуры данных после  -й операции (
-й операции ( 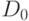 — исходное
состояние).
Потенциал представляет собой функцию
— исходное
состояние).
Потенциал представляет собой функцию  из множества возможных состояний
структуры данных в множество действительных чисел.
из множества возможных состояний
структуры данных в множество действительных чисел.
Пусть  — реальная стоимость
— реальная стоимость  -й
операции. Учетной стоимостью
-й
операции. Учетной стоимостью  -й операции объявим
число
-й операции объявим
число 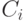 , определяемое формулой
, определяемое формулой
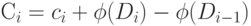
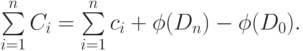
Если нам удалось придумать функцию  , для которой
, для которой
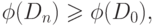
 операций. Не ограничивая общности, можно
считать, что
операций. Не ограничивая общности, можно
считать, что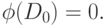
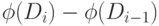
 -й операции включает в себя
резерв (предоплату за будущие операции); если же эта разность
отрицательна, то учетная стоимость
-й операции включает в себя
резерв (предоплату за будущие операции); если же эта разность
отрицательна, то учетная стоимость  -й операции меньше реальной
и разница покрывается за счет накопленного к этому моменту потенциала.
-й операции меньше реальной
и разница покрывается за счет накопленного к этому моменту потенциала.Учетные стоимости и оценки реальной стоимости, рассчитанные с помощью метода потенциалов, зависят от выбора потенциальной функции, а сам этот выбор является делом творческим.
Ниже эти три метода будут проиллюстрированы на примере анализа работы двоичного счетчика с единственной операцией Increment (прибавление единицы).
