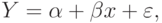|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Парный регрессионный анализ
2.1. Основные понятия регрессионного анализа
Регрессионный анализ является одним из наиболее распространенных инструментов эконометрического анализа. Он позволяет проанализировать и оценить связи между зависимой (объясняемой) и независимыми (объясняющими) переменными. Зависимую переменную иногда называют результативным признаком, а объясняющие переменные - предикторами, регрессорами или факторами. Как это часто бывает, название этого метода не связано с его сутью, а имеет исторические корни. Термин "регрессия" ввел лорд Ф. Гальтон (1822-1911), исследуя связь между ростом родителей и детей. Он установил, что хотя у высоких родителей - высокие дети, а у невысоких чаще рождаются маленькие дети, рост детей имеет тенденцию к постепенному выравниванию, т.е. стремится к средним значениям. Будучи аристократом, Ф. Гальтон к такой тенденции относился негативно и потому назвал ее регрессией (упадком).
Обозначим зависимую (объясняемую) переменную как  , а независимые (объясняющие) переменные как
, а независимые (объясняющие) переменные как 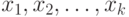 . Если
. Если 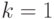 и есть только одна независимая переменная
и есть только одна независимая переменная  (которую обозначим
(которую обозначим  ), то регрессия называется простой (simple), или парной. Если
), то регрессия называется простой (simple), или парной. Если 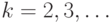 то регрессия называется множественной.
то регрессия называется множественной.
Теперь обратимся к вопросам, связанным с априорными предположениями, оценкой коэффициентов и доверительными интервалами для прогноза парной регрессии.
Начнем с построения простейшей модели
где  - зависимая переменная, состоящая из двух слагаемых: 1) неслучайной составляющей
- зависимая переменная, состоящая из двух слагаемых: 1) неслучайной составляющей  (
( - независимая переменная,
- независимая переменная,  и
и  - постоянные числа - параметры уравнения); 2) случайного члена
- постоянные числа - параметры уравнения); 2) случайного члена  .
.
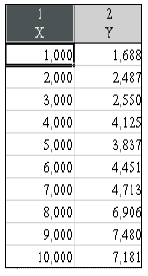
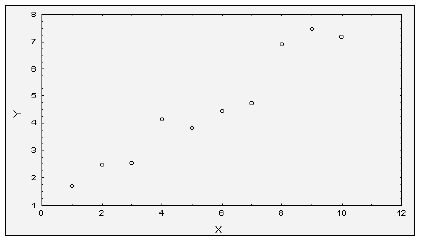
Допустим, мы имеем данные, представленные в двух видах: табличном (табл. 2.1) и графическом (рис. 2.1). Предположим, что истинная зависимость между  и
и  - линейная, т.е. существует некая прямая
- линейная, т.е. существует некая прямая  , отражающая "истинную" зависимость. Задача регрессионного анализа состоит в получении оценок
, отражающая "истинную" зависимость. Задача регрессионного анализа состоит в получении оценок 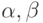 , а следовательно, и положения прямой. На рисунке 2.2 такое уравнение построено с помощью пакета STATISTICA.
, а следовательно, и положения прямой. На рисунке 2.2 такое уравнение построено с помощью пакета STATISTICA.
Таблица 2.1
Существование отклонений от прямой регрессии, т.е. случайных слагаемых  , объясняется рядом причин. К ним относятся:
, объясняется рядом причин. К ним относятся:
- ошибки измерения. Например, при сборе данных об урожайности сельскохозяйственных культур, результаты работы в отчетах могут завышаться или занижаться в зависимости от экономической политики, или оцениваться "на глазок" и т.д.;
-
невключение объясняющих переменных. Возможно, что простая зависимость
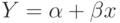 является очень большим упрощением. Наверняка существуют и другие влияющие на изменение
является очень большим упрощением. Наверняка существуют и другие влияющие на изменение  , факторы, которые не удалось оценить и включить в уравнение;
, факторы, которые не удалось оценить и включить в уравнение; - неправильный выбор вида зависимости в уравнении. Возможно, зависимость не линейная, а более сложная. Приведем наиболее употребительные виды связей, используемые при построении парной регрессии:
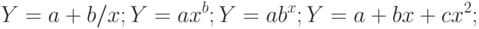
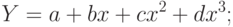
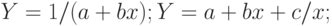
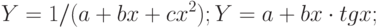

Вид зависимости выбирают либо графически, либо проверяя качество моделей на контрольной выборке, либо используя априорные экономические соображения. Например, валовой выпуск продукции  в зависимости от числа занятых в производстве работников
в зависимости от числа занятых в производстве работников  может быть описан уравнением
может быть описан уравнением 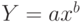 , где
, где 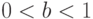 . Разделив уравнение слева и справа на
. Разделив уравнение слева и справа на  , получим зависимость производительности труда от числа работников в производстве:
, получим зависимость производительности труда от числа работников в производстве:  , где
, где 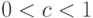 ;
;
- отражение уравнением регрессии связи между агрегированными переменными. Например, зависимость между урожайностью и количеством внесенных удобрений индивидуальна для различных полей, и любая попытка определить зависимость между совокупным урожаем и совокупным внесением удобрений является лишь приближением (аппроксимацией).
Для оценки параметров 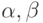 обычно применяют метод наименьших квадратов (МНК). Существуют и другие методы оценки параметров, например: метод моментов, метод наименьших модулей, метод максимального правдоподобия.
обычно применяют метод наименьших квадратов (МНК). Существуют и другие методы оценки параметров, например: метод моментов, метод наименьших модулей, метод максимального правдоподобия.