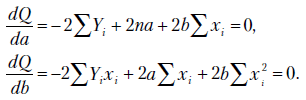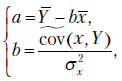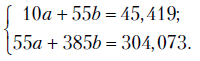|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Парный регрессионный анализ
2.2. Регрессия по методу наименьших квадратов (МНК)
Если имеется n наблюдений, уравнение (2.1) можно представить в следующем виде:

Случайное слагаемое  можно рассматривать как последовательность
можно рассматривать как последовательность  случайных величин
случайных величин  .
.
Метод наименьших квадратов позволяет получить такие оценки  и
и  параметров
параметров  и
и  , при которых сумма квадратов отклонений
, при которых сумма квадратов отклонений  фактических значений признака
фактических значений признака  от расчетных (теоретических)
от расчетных (теоретических)  является минимальной:
является минимальной:
Найдем минимум функции  , приравняв производные по каждой переменной
, приравняв производные по каждой переменной  к нулю:
к нулю:
После преобразований получаем систему уравнений
Система уравнений (2.4) представляет собой систему нормальных уравнений МНК.
Решая систему уравнений (2.4), находим  и
и 
где 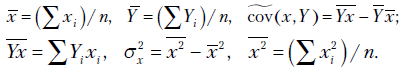
Коэффициент  при
при  называется выборочным коэффициентом регрессии. Если переменную
называется выборочным коэффициентом регрессии. Если переменную  изменить на единицу, т.е. взять за
изменить на единицу, т.е. взять за  величину
величину 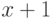 , то новое значение
, то новое значение 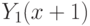 будет равно
будет равно  . Следовательно, коэффициент регрессии показывает среднее изменение результата
. Следовательно, коэффициент регрессии показывает среднее изменение результата  при изменении фактора
при изменении фактора  на единицу.
на единицу.
Коэффициент  указывает на значение результирующего признака при нулевом значении фактора. Это важный индикатор для выбора вида уравнения регрессии. Например, если в результате вычислений коэффициент
указывает на значение результирующего признака при нулевом значении фактора. Это важный индикатор для выбора вида уравнения регрессии. Например, если в результате вычислений коэффициент  оказался отрицательным, а экономический смысл задачи диктует положительность или равенство нулю показателя
оказался отрицательным, а экономический смысл задачи диктует положительность или равенство нулю показателя  , значит, выбор вида уравнения был неудачен.
, значит, выбор вида уравнения был неудачен.
Произведем расчеты для данных, представленных в табл. 2.1.
Систему уравнений (2.4) для данных табл. 2.2 представим в виде
Таблица 2.2
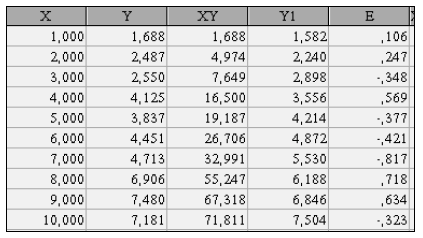
Решив последнюю систему уравнений, получим  . Построим таблицу (табл. 2.3), содержащую исходные данные, расчетные значения
. Построим таблицу (табл. 2.3), содержащую исходные данные, расчетные значения 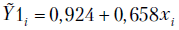 и остатки
и остатки 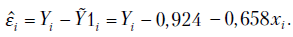
Таблица 2.3