| Россия, Пошатово |
Синтаксический разбор слева направо (LR)
16.4.3. Как изменится определение согласованности?
Решение. Слово S из терминалов и нетерминалов
согласовано с ситуацией ![[{K}\to{U}\_{V},\,{t}]](/sites/default/files/tex_cache/aa6544ad7e9e7ca599981058e2a47196.png) (здесь t - терминал или EOI ), если S кончается на U,
то есть
(здесь t - терминал или EOI ), если S кончается на U,
то есть 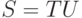 , и, кроме того, T принадлежит
, и, кроме того, T принадлежит 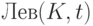 .
.
16.4.4.
Каковы правила для индуктивного вычисления множества  ситуаций, согласованных с данным словом S?
ситуаций, согласованных с данным словом S?
Ответ.
(1) Если слово S согласовано с ситуацией [K->U_V,t], причем слово V начинается на букву J, то есть V=JW, то слово SJ согласовано с ситуацией [K->UJ_W,t].
Это правило полностью определяет все ситуации с непустой
левой половиной (то есть не начинающиеся с подчеркивания),
согласованные с SJ. Осталось определить, для каких
нетерминалов K и терминалов t слово SJ принадлежит 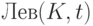 . Это делается по двум правилам:
. Это делается по двум правилам:
(2) Если ситуация [L->U\_V,t] согласована с SJ (согласно Правилу (1)), а V начинается на нетерминал K, то SJ принадлежит Лев(K,s) для всех терминалов s, которые могут начинать слова, выводимые из слова V\K (слово V без первой буквы K ), а также для s=t, если из V\K выводится пустое слово.
(3) Если SJ входит в Лев(L,t) для некоторых L и t, причем L->V - правило грамматики и V начинается на нетерминал K, то SJ принадлежит Лев(K,s) для всех терминалов s, которые могут начинать слова, выводимые из V\K, а также для s=t, если из V\K выводится пустое слово.
16.4.5. Дать определения LR(1)-конфликтов сдвиг/свертка и свертка/свертка по аналогии с данными выше.
Решение. Пусть дана некоторая грамматика. Пусть S - произвольное слово из терминалов и нетерминалов. Если множество  содержит ситуацию, в которой справа от подчеркивания стоит терминал t, то говорят, что для пары
содержит ситуацию, в которой справа от подчеркивания стоит терминал t, то говорят, что для пары  возможен сдвиг. (Это определение не изменилось по сравнению с SLR(1)-случаем - вторые компоненты пар из
возможен сдвиг. (Это определение не изменилось по сравнению с SLR(1)-случаем - вторые компоненты пар из  не учитываются.)
не учитываются.)
Если в  есть ситуация, в которой справа от подчеркивания ничего нет, а вторым членом пары является терминал t, то говорят, что для пары
есть ситуация, в которой справа от подчеркивания ничего нет, а вторым членом пары является терминал t, то говорят, что для пары  LR(1)-возможна свертка (по соответствующему правилу). Говорят, что для пары
LR(1)-возможна свертка (по соответствующему правилу). Говорят, что для пары  возникает
LR(1)-конфликт типа сдвиг/свертка,
если возможны и сдвиг, и свертка. Говорят, что для пары
возникает
LR(1)-конфликт типа сдвиг/свертка,
если возможны и сдвиг, и свертка. Говорят, что для пары  возникает LR(1)-конфликт типа свертка/свертка, если есть несколько правил, по которым возможна свертка.
возникает LR(1)-конфликт типа свертка/свертка, если есть несколько правил, по которым возможна свертка.
Грамматика называется LR(1)-грамматикой, если в ней нет LR(1)-конфликтов типа сдвиг/свертка и свертка/свертка ни для одной пары  .
.
16.4.6. Построить алгоритм проверки выводимости слова в LR(1)-грамматике.
Решение. Как и раньше, на каждом шаге LR-процесса можно однозначно определить, какой шаг только и может быть следующим.
Полезно (в частности, для LALR(1)-разбора, смотри ниже) понять, как связаны понятия LR(0) и LR(1)-согласованности.
16.4.7. Сформулировать и доказать соответствующее утверждение.
Ответ. Пусть фиксирована некоторая грамматика. Слово S из терминалов и нетерминалов является LR(0)-согласованным с ситуацией 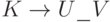 тогда и только тогда, когда оно LR(1)-согласовано с парой
тогда и только тогда, когда оно LR(1)-согласовано с парой ![[{K}\to{U}\_{V},{t}]](/sites/default/files/tex_cache/6ea27d1957c8e92c3b9138c1e02bb9bb.png) для некоторого
терминала t (или для
для некоторого
терминала t (или для 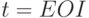 ). То же самое
другими словами:
). То же самое
другими словами:  есть объединение
есть объединение 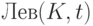 по всем t. В последней форме это
совсем ясно.
по всем t. В последней форме это
совсем ясно.
Замечание. Таким образом, функция  в LR(1)-смысле является расширением функции
в LR(1)-смысле является расширением функции  в LR(0)-смысле:
в LR(0)-смысле:  получается из
получается из  , если во
всех парах выбросить вторые члены.
, если во
всех парах выбросить вторые члены.
Теперь мы можем дать определение LALR(1)-грамматики. Пусть фиксирована некоторая грамматика, S - слово из нетерминалов и терминалов, t - некоторый терминал (или EOI ). Будем говорить, что для пары  LALR(1)-возможна свертка по
некоторому правилу, если существует другое слово
LALR(1)-возможна свертка по
некоторому правилу, если существует другое слово 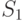 с
с  , причем для пары
, причем для пары 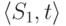 LR(1)-возможна свертка по
рассматриваемому правилу. Далее определяются конфликты
(естественным образом), и грамматика называется LALR(1)-грамматикой, если конфликтов нет.
LR(1)-возможна свертка по
рассматриваемому правилу. Далее определяются конфликты
(естественным образом), и грамматика называется LALR(1)-грамматикой, если конфликтов нет.
16.4.8. Доказать, что всякая SLR(1)-грамматика является LALR(1)-грамматикой, а всякая LALR(1)-грамматика является LR(1)-грамматикой.
Указание. Это - простое следствие определений.
16.4.9. Построить алгоритм проверки выводимости в LALR(1)-грамматике, который хранит в стеке меньше информации, чем соответствующий LR(1)-алгоритм.
Указание.
Достаточно хранить в стеке множества  , поскольку согласно определению LALR(1)-возможность свертки ими определяется. (Так что сам алгоритм ничем не отличается от SLR(1)-случая, кроме таблицы возможных сверток.)
, поскольку согласно определению LALR(1)-возможность свертки ими определяется. (Так что сам алгоритм ничем не отличается от SLR(1)-случая, кроме таблицы возможных сверток.)
16.4.10. Привести пример LALR(1)-грамматики, которая не является SLR(1)-грамматикой.
16.4.11. Привести пример LR(1)-грамматики, которая не является LALR(1)-грамматикой.
16.5. Общие замечания о разных методах разбора
Применение этих методов на практике имеет свои хитрости и тонкости, которых мы не касались. (Например, таблицы следует хранить по возможности экономно.) Часто оказывается также, что для некоторого входного языка наиболее естественная грамматика не является LL(1)-грамматикой, но является LR(1)-грамматикой, а также может быть заменена на LL(1)-грамматику без изменения языка. Какой из этих вариантов выбрать, не всегда ясно. Дилетантский совет: если Вы сами проектируете входной язык, то не следует выпендриваться и употреблять одни и те же символы для разных целей - и тогда обычно несложно написать LL(1)-грамматику или рекурсивный анализатор. Если же входной язык задан заранее с помощью LR(1)-грамматики, не являющейся LL(1)-грамматикой, то лучше ее не трогать, а разбирать как есть. При этом могут оказаться полезные средства автоматического порождения анализаторов, наиболее известными из которых являются yacc (UNIX) и bison (GNU).
Большое количество полезной и хорошо изложенной информации о теории и практике синтаксического разбора имеется в книге Ахо, Сети и Ульмана (см. список книг для чтения).
