| Россия, Пошатово |
Инспектор
Вы можете этот курс.
Опубликован: 08.04.2009 | Уровень: для всех | Доступ: платный
Лекция 16:
Синтаксический разбор слева направо (LR)
16.2. LR(0)-грамматики
Напомним, что наша основная цель - это поиск вывода заданного слова, или, другими словами, поиск успешного LR-процесса над ним. Во всех рассматриваемых нами грамматиках успешный LR-процесс (над данным словом) единствен. Искать этот единственный успешный процесс мы будем постепенно: в каждый момент мы смотрим, какой шаг возможен следующим. Для этого на грамматику надо наложить дополнительные требования, и сейчас мы рассмотрим простейший случай так называемых LR(0)-грамматик. Мы уже знаем:
(1) В успешном LR-процессе возможна свертка по правилу K->U при содержимом стека S тогда и только тогда, когда S принадлежит ЛевКонт(K->U) или, другими словами, когда слово S согласовано с ситуацией K->U_.
Аналогичное утверждение про сдвиг гласит:
(2) В успешном LR-процессе при содержимом стека S возможен сдвиг с очередным символом a тогда и только тогда, когда S согласовано с некоторой ситуацией K->U_aV.
16.2.1. Доказать это.
Указание. Пусть произошел сдвиг и к стеку S добавилась буква a. Рассмотрите первую свертку, затрагивающую эту букву.
Рассмотрим некоторую грамматику и произвольное слово S из терминалов и нетерминалов. Если множество 
содержит ситуацию, в которой справа от подчеркивания стоит терминал, то говорят, что для
слова S возможен сдвиг. Если в есть ситуация, в которой справа от подчеркивания ничего нет, то
говорят, что для слова S возможна свертка (по соответствующему правилу). Говорят, что для слова S возникает конфликт типа сдвиг/свертка, если возможны и сдвиг, и свертка. Говорят, что для слова S возникает конфликт типа свертка/свертка, если есть несколько правил, по которым возможна свертка.
Грамматика называется LR(0)-грамматикой, если в ней нет конфликтов типа сдвиг/свертка и свертка/свертка ни для одного слова S.
16.2.2. Является ли приведенная выше грамматика LR(0)-грамматикой?
Решение. Нет, не является. Для слов T и E+T имеются конфликты типа сдвиг/свертка.
16.2.3. Являются ли LR(0)-грамматиками такие:
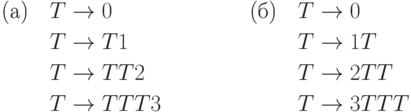
Решение. Являются, см. таблицы ниже (конфликтов нет).
| Слово S | Сост (S) |
|---|---|
| пустое | T->_0 T->_T1 T->_TT2 T->_TTT3 |
| 0 | T->0_ |
| T |
T->T_1 T->T_T2 T->T_TT3 T->_0 T->_T1 T->_TT2 T->_TT3 |
| T1 | T->T1_ |
| TT |
T->TT_2 T->TT_T3 T->T_1 T->T_T2 T->T_TT3 T->_0 T->_T1 T->_TT2 T->_TTT3 |
| TT2 | T->TT2_ |
| TTT |
T->TTT_3 T->TT_2 T->TT_T3 T->T_1 T->T_T2 T->T_TT3 T->_0 T->_T1 T->)TT2 T->_TTT3 |
| TT0 | =0 |
| TTT3 | T->TTT3_ |
| TTT2 | =TT2 |
| TTTT | =TTT |
| TTT0 | =0 |
| Слово S | Сост (S) |
|---|---|
| пустое | T->_0 T->_1T T->_1TT T->_3TTT |
| 0 | T->0_ |
| 1 |
T->1_T T->_0 T->_1T T->_2TT T->_3TTT |
| 2 |
T->2_TT T->_0 T->_1T T->_2TT T->_3TTT |
| 3 |
T->3_TTT T->_0 T->_1T T->_2TT T->_3TTT |
| 1T | T->1T_ |
| 10 | =0 |
| 11 | =1 |
| 12 | =2 |
| 13 | =3 |
| 2T |
T->2T_T T->_0 T->_1T T->_2TT T->_3TTT |
| 20 | =0 |
| 21 | =1 |
| 22 | =2 |
| 23 | =3 |
| 3T |
T->3T_TT T->_0 T->_1T T->_2TT T->_3TTT |
| 30 | =0 |
| 31 | =1 |
| 32 | =2 |
| 33 | =3 |
| 2TT | T->2TT_ |
| 2T0 | =0 |
| 2T1 | =1 |
| 2T2 | =2 |
| 2T3 | =3 |
| 3TT |
T->3TT_T T->_0 T->_1T T->_2TT T->_3TTT |
| 3T0 | =0 |
| 3T1 | =1 |
| 3T2 | =2 |
| 3T3 | =3 |
| 3TTT | T->3TTT_ |
| 3TTT0 | =0 |
| 3TTT1 | =1 |
| 3TTT2 | =2 |
| 3TTT3 | =3 |
Эта задача показывает, что LR(0)-грамматики могут быть как леворекурсивными, так и праворекурсивными.
16.2.4. Пусть дана LR(0)-грамматика. Доказать, что у любого слова существует не более одного правого вывода. Построить алгоритм проверки выводимости в LR(0)-грамматике.
Решение. Пусть дано произвольное слово. Будем строить LR-процесс над ним по шагам. Пусть текущее состояние стека LR-процесса равно S. Нам надо решить, делать сдвиг или свертку (и если свертку, то по какому правилу). Согласно определению LR(0)-грамматики, в нашем состоянии S возможен либо только сдвиг, либо только свертка (причем лишь по одному правилу). Таким образом, поиск возможных продолжений LR-процесса происходит детерминированно (на каждом шаге можно определить, какое действие только и возможно).
16.2.5. Что произойдет, если анализируемое слово не имеет вывода в данной грамматике?
Ответ. Либо на некотором шаге не будет возможен ни сдвиг, ни свертка, либо все возможные сдвиги будет иметь неподходящий очередной символ.
Замечания. 1. При реализации этого алгоритма нет необходимости каждый раз заново вычислять множество для текущего значения S. Эти множества
можно также хранить в стеке (в каждый момент хранятся множества 
для всех начал T текущего слова S ).
2. На самом деле само слово S можно не хранить -
достаточно хранить множества ситуаций для всех
его начал T (включая само S ).
В алгоритме проверки выводимости в LR(0)-грамматике мы используем не всю информацию, которую могли бы. В этом алгоритме для каждого состояния известно заранее, что в нем возможен только сдвиг или только свертка (причем в последнем случае известно, по какому правилу). Более изощренный алгоритм мог бы принимать решение о выборе между сдвигом и сверткой, посмотрев на очередной символ ( Next ). Глядя на состояние, можно сказать, при каких значениях Next возможен сдвиг (это те терминалы, которые в ситуациях этого состояния стоят непосредственно за подчеркиванием). Сложнее воспользоваться информацией о символе Next для решения вопроса о том, возможна ли свертка. Для этого есть упрощенный метод (грамматики, к которым он применим, называют SLR(1)-грамматиками [сокращение от Simple LR(1)]) и полный метод (более сложный, но использующий всю возможную информацию; грамматики, к которым он применим, называют LR(1)-грамматиками). Есть и промежуточный класс грамматик, называемый LALR(1).
