| Россия, Пошатово |
Сопоставление с образцом
10.8. Суффиксные деревья
До сих про наши программы сначала получали образец, который надо искать, а потом текст, в котором надо искать. В следующих задачах все наоборот.
10.8.1.
Программа получает на вход слово  длины
длины  и может
его
обрабатывать (пока без ограничений на время и память).
Затем она получает слово
и может
его
обрабатывать (пока без ограничений на время и память).
Затем она получает слово  длины
длины  и должна сообщить,
является ли оно подсловом слова
и должна сообщить,
является ли оно подсловом слова  . При этом число
операций при обработке слова
. При этом число
операций при обработке слова  должно быть порядка
должно быть порядка  (не превосходить
(не превосходить 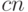 , где константа
, где константа  может зависеть
от размера алфавита). Как написать такую программу?
может зависеть
от размера алфавита). Как написать такую программу?
Решение. Пока не накладывается никаких ограничений на
время и память при обработке  , это не представляет
труда. Именно, надо склеить все подслова слова
, это не представляет
труда. Именно, надо склеить все подслова слова  в дерево, объединив слова с общими началами (как мы это делали,
распознавая вхождения нескольких образцов). Например, для
в дерево, объединив слова с общими началами (как мы это делали,
распознавая вхождения нескольких образцов). Например, для  получится такое дерево подслов (на ребре написана
буква, которая добавляется при движении по этому ребру;
вершины находятся во взаимно однозначном соответствии
с подсловами слова
получится такое дерево подслов (на ребре написана
буква, которая добавляется при движении по этому ребру;
вершины находятся во взаимно однозначном соответствии
с подсловами слова  ):
):
Пусть такое дерево построено. После этого, читая слово  слева направо, мы прослеживаем
слева направо, мы прослеживаем  в дереве, начав с корня;
слово
в дереве, начав с корня;
слово  будет подсловом слова
будет подсловом слова  , если при этом мы не
выйдем за пределы дерева.
, если при этом мы не
выйдем за пределы дерева.
Заметим, что аналогичная конструкция годится для любого
множества слов  , а не только для множества всех подслов
данного слова: после того как соответствующее дерево
построено, мы можем про любое слово
, а не только для множества всех подслов
данного слова: после того как соответствующее дерево
построено, мы можем про любое слово  определить его
принадлежность к
определить его
принадлежность к  за время, пропорциональное
длине
за время, пропорциональное
длине  .
(Надо только дополнительно хранить в вершине дерева
информацию, принадлежит ли соответствующее ей слово
множеству
.
(Надо только дополнительно хранить в вершине дерева
информацию, принадлежит ли соответствующее ей слово
множеству  или лишь является началом другого слова,
принадлежащего
или лишь является началом другого слова,
принадлежащего  .)
.)
10.8.2.
Решить предыдущую задачу с дополнительным ограничением:
объем используемой памяти пропорционален длине слова  .
.
Решение. Прежний способ не годится: число вершин дерева
равно числу подслов слова  , а у слова длины
, а у слова длины  число
подслов может быть порядка
число
подслов может быть порядка 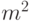 , а не
, а не  . Однако мы
можем "сжать" наше дерево, оставив вершинами лишь точки
ветвления (где больше одного сына). Тогда на ребрах дерева
надо написать уже не буквы, а куски слова
. Однако мы
можем "сжать" наше дерево, оставив вершинами лишь точки
ветвления (где больше одного сына). Тогда на ребрах дерева
надо написать уже не буквы, а куски слова  .
.
Вот что получится при сжатии нашего примера:
Будем считать (здесь и далее), что последняя буква
слова  больше в нем не встречается. (Этого всегда можно
достичь, дописав дополнительный фиктивный символ.) Тогда
листья сжатого дерева соответствуют концам слова
больше в нем не встречается. (Этого всегда можно
достичь, дописав дополнительный фиктивный символ.) Тогда
листья сжатого дерева соответствуют концам слова  ,
а внутренние вершины (точки ветвления) - таким
подсловам
,
а внутренние вершины (точки ветвления) - таким
подсловам  слова
слова  , которые встречаются
в
, которые встречаются
в  несколько раз, и притом с разными буквами после
несколько раз, и притом с разными буквами после  .
.
У каждой внутренней вершины (не листа) сжатого дерева есть
не менее двух сыновей. В деревьях с такими свойствами число
внутренних вершин не превосходит числа листьев. (В самом
деле, при движении слева направо в каждой точке ветвления
добавляется новый путь к листу.) Поскольку листьев  ,
всего вершин не более
,
всего вершин не более 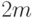 , и мы уложимся в линейную
по
, и мы уложимся в линейную
по  память, если будем экономно хранить пометки на ребрах.
Каждая такая пометка является подсловом слова
память, если будем экономно хранить пометки на ребрах.
Каждая такая пометка является подсловом слова  , и потому
достаточно указывать координату ее начала и конца в
, и потому
достаточно указывать координату ее начала и конца в  .
Это не помешает впоследствии прослеживать произвольное
слово
.
Это не помешает впоследствии прослеживать произвольное
слово  в этом дереве буква за буквой, просто в некоторые
моменты мы будем находиться внутри ребер (и должны помнить,
внутри какого ребра и в какой позиции мы находимся). При
появлении новой буквы слова
в этом дереве буква за буквой, просто в некоторые
моменты мы будем находиться внутри ребер (и должны помнить,
внутри какого ребра и в какой позиции мы находимся). При
появлении новой буквы слова  ее нужно сравнить
с соответствующей буквой пометки этого ребра (что можно
сделать за
ее нужно сравнить
с соответствующей буквой пометки этого ребра (что можно
сделать за  действий, так как координату этой буквы
мы знаем.)
действий, так как координату этой буквы
мы знаем.)
Построенное нами сжатое дерево называют сжатым
суффиксным деревом }
слова  (концы слова называют "суффиксами").
(концы слова называют "суффиксами").
10.8.3.
Показать, что построение сжатого суффиксного дерева можно
выполнить за время  с использованием
с использованием  памяти.
памяти.
Решение. Будем добавлять в суффиксное дерево суффиксы по очереди. Добавление очередного суффикса делается так же, как и проверка принадлежности: мы читаем его буква за буквой и прокладываем путь в дереве. В некоторый момент добавляемый суффикс выйдет за пределы дерева (напомним, что мы считаем, что последний символ слова уникален).
Если это произойдет посередине ребра, то ребро придется
в этом месте разрезать. Ребро превратится в два, его
пометка разрежется на две, появится новая вершина (точка
ветвления) и ее новый сын-лист. Если точка ветвления
совпадет с уже имевшейся в дереве, то у нее появится новый
сын-лист. В любом случае после обнаружения места
ветвления требуется  операций для перестройки дерева
(в частности, разрезание пометки на две выполняется легко,
так как пометки хранятся в виде координат начала и конца
в слове
операций для перестройки дерева
(в частности, разрезание пометки на две выполняется легко,
так как пометки хранятся в виде координат начала и конца
в слове  ).
).
Гораздо более сложной задачей является построение сжатого суффиксного дерева за линейное время (вместо квадратичного, как в предыдущей задаче). Чтобы изложить алгоритм МакКрейта, который решает эту задачу, нам понадобятся некоторые приготовления.
Для начала опишем более подробно структуру дерева, которое мы используем, и операции с ним.
Мы рассматриваем деревья с корнем, на ребрах которых
написаны слова (пометки); все пометки являются подсловами
некоторого заранее фиксированного слова  . При этом
выполнены такие свойства:
. При этом
выполнены такие свойства:
- каждая внутренняя вершина имеет хотя бы двух сыновей;
- пометки на ребрах, выходящих из данной вершины, начинаются на разные буквы.
Каждой вершине  такого дерева соответствует слово,
которое записано на пути от корня
такого дерева соответствует слово,
которое записано на пути от корня  к вершине
к вершине  .
Будем обозначать это слово
.
Будем обозначать это слово 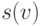 . Обозначим пометку на ребре,
ведущем к
. Обозначим пометку на ребре,
ведущем к  , через
, через  , а отца
вершины
, а отца
вершины  - через
- через  . Тогда
. Тогда  (пустое слово), а
(пустое слово), а
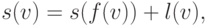
 (знак "
(знак " 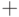 "
обозначает соединение строк).
"
обозначает соединение строк).Помимо вершин дерева, мы будем рассматривать позиции в нем, которые могут быть расположены в вершинах, а также "внутри ребер" (разделяя пометку этого ребра на две
части). Формально говоря, позиция представляет собой пару 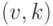 , где
, где  - вершина (отличная от корня),
а
- вершина (отличная от корня),
а  - целое число в промежутке
- целое число в промежутке  ,
указывающее, на сколько букв надо вернуться от
,
указывающее, на сколько букв надо вернуться от  к корню.
Здесь
к корню.
Здесь  - длина пометки
- длина пометки  ; значение
; значение 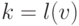 соответствовало бы предыдущей вершине и потому не
допускается. К числу позиций мы добавляем также пару
соответствовало бы предыдущей вершине и потому не
допускается. К числу позиций мы добавляем также пару 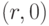 , соответствующую корню дерева. Каждой позиции
, соответствующую корню дерева. Каждой позиции 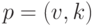 соответствует слово
соответствует слово  , которое получается удалением
, которое получается удалением  последних символов из
последних символов из 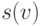 .
.
Пусть  - произвольная позиция в дереве, а
- произвольная позиция в дереве, а  -
слово.
Пройти вдоль
-
слово.
Пройти вдоль  , начиная с
, начиная с  , означает найти другую позицию
, означает найти другую позицию  , для которой
, для которой 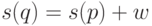 . Если такая позиция есть, то (при описанном способе хранения пометок, когда указываются координаты их начала и конца внутри
. Если такая позиция есть, то (при описанном способе хранения пометок, когда указываются координаты их начала и конца внутри  ) ее
можно найти за время, пропорциональное длине слова
) ее
можно найти за время, пропорциональное длине слова  .
Если такой позиции нет, то в какой-то момент мы "свернем с пути"; в этот момент можно пополнить дерево,
сделав отсутствующую в дереве часть слова
.
Если такой позиции нет, то в какой-то момент мы "свернем с пути"; в этот момент можно пополнить дерево,
сделав отсутствующую в дереве часть слова  пометкой на
пути к новому листу. Надо только, чтобы эта пометка была
подсловом слова
пометкой на
пути к новому листу. Надо только, чтобы эта пометка была
подсловом слова  (при нашем способе хранения пометок);
это будет гарантировано, если прослеживаемое слово
(при нашем способе хранения пометок);
это будет гарантировано, если прослеживаемое слово  является подсловом слова
является подсловом слова  .
.
Заметим, что при этом может образоваться новая вершина (если развилка оказалась внутри ребра), а может и не образоваться (если развилка оказалась в вершине). Число действий при такой модификации пропорционально длине пройденной части слова (длина непройденной не важна).
Оказывается, что навигацию в дереве можно ускорить, если заранее известно, что она будет успешной.
10.8.4.
Пусть для данной позиции  и слова
и слова  заранее
известно, что в дереве есть позиция
заранее
известно, что в дереве есть позиция  , для которой
, для которой 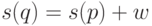 .
Показать, что позицию
.
Показать, что позицию  можно найти за время,
пропорциональное числу ребер дерева на пути от
можно найти за время,
пропорциональное числу ребер дерева на пути от  к
к  .
(Это число может быть значительно меньше длины слова
.
(Это число может быть значительно меньше длины слова  ,
если пометки на ребрах длинные.)
,
если пометки на ребрах длинные.)
Решение. В самом деле, при навигации нужно ориентироваться лишь в вершинах (выбирать исходящее ребро в зависимости от очередной буквы); в остальных местах путь однозначный и потому можно сдвигаться сразу к концу ребра.


