Сопоставление с образцом

10.5. Алгоритм Бойера- Мура

Этот алгоритм делает то, что на первый взгляд кажется невозможным: в типичной ситуации он читает лишь небольшую часть всех букв слова, в котором ищется заданный образец. Как так может быть? Идея проста. Пусть, например, мы ищем образец abcd. Посмотрим на четвертую букву слова: если, к примеру, это буква e, то нет никакой необходимости читать первые три буквы. (В самом деле, в образце буквы e нет, поэтому он может начаться не раньше пятой буквы.)

Мы приведем самый простой вариант этого алгоритма, который не гарантирует быстрой работы во всех случаях. Пусть - образец, который надо искать. Для каждого символа s найдем самое правое его вхождение в слово X, то есть наибольшее k, при котором . Эти сведения будем хранить в массиве pos[s] ; если символ s вовсе не встречается, то нам будет удобно положить (мы увидим дальше, почему).

10.5.1. Как заполнить массив pos?

Решение.

положить все pos[s] равными 0
for i:=1 to n do begin
  pos[x[i]]:=i;
end;

В процессе поиска мы будем хранить в переменной last номер буквы в слове, против которой стоит последняя буква образца. Вначале 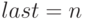(длина образца), затем last постепенно увеличивается.

last:=n;
{все предыдущие положения образца уже проверены}
while last <= m do begin {слово не кончилось}
| if x[n] <> y[last] then begin {последние буквы разные}
| | last := last + (n - pos[y[last]]);
| | {n - pos[y[last]]  - это минимальный сдвиг образца,
| |    при котором напротив y[last] встанет такая же
| |    буква в образце. Если такой буквы нет вообще,
| |    то сдвигаем на всю длину образца}
| end else begin
| | если нынешнее положение подходит, т.е. если
| | x[1]..x[n] = y[last-n+1]..y[last],
| | то сообщить о совпадении;
| | last := last+1;
| end;
end;

Знатоки рекомендуют проверку совпадения проводить справа налево, т.е. начиная с последней буквы образца (в которой совпадение заведомо есть). Можно также немного сэкономить, произведя вычитание заранее и храня не pos[s], а n-pos[s], т.е. число букв в образце справа от последнего вхождения буквы s.

Возможны разные модификации этого алгоритма. Например, можно строку last:=last+1 заменить на last:=last+(n-u), где u - координата второго справа вхождения буквы x[n] в образец.

10.5.2. Как проще всего учесть это в программе?

Решение. При построении таблицы pos написать

for i:=1 to n-1 do...

(далее как раньше), а в основной программе вместо last:=last+1 написать

last:= last+n-pos[y[last]];

Приведенный нами упрощенный вариант алгоритма Бойера-Мура в некоторых случаях требует существенно больше n действий (число действий порядка mn ), проигрывая алгоритму Кнута-Морриса-Пратта.

10.5.3. Привести пример ситуации, в которой образец не входит в слово, но алгоритму требуется порядка mn действий, чтобы это установить.

Решение. Пусть образец имеет вид 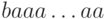, а само слово состоит только из букв a. Тогда на каждом шаге несоответствие выясняется лишь в последний момент.

Настоящий (не упрощенный) алгоритм Бойера-Мура гарантирует, что число действий не превосходит в худшем случае. Он использует идеи, близкие к идеям алгоритма Кнута-Морриса-Пратта. Представим себе, что мы сравнивали образец со входным словом, идя справа налево. При этом некоторый кусок (являющийся концом образца) совпал, а затем обнаружилось различие: перед в образце стоит не то, что во входном слове. Что можно сказать в этот момент о входном слове? В нем обнаружен фрагмент, равный , а перед ним стоит не та буква, что в образце. Эта информация может позволить сдвинуть образец на несколько позиций вправо без риска пропустить его вхождение. Эти сдвиги следует вычислить заранее для каждого конца нашего образца. Как говорят знатоки, все это (вычисление таблицы сдвигов и ее использование) можно уложить в действий.

10.6. Алгоритм Рабина

Этот алгоритм основан на простой идее. Представим себе, что в слове длины мы ищем образец длины . Вырежем окошечко размера и будем двигать его по входному слову. Нас интересует, не совпадает ли слово в окошечке с заданным образцом. Сравнивать по буквам долго. Вместо этого фиксируем некоторую функцию, определенную на словах длины . Если значения этой функции на слове в окошечке и на образце различны, то совпадения нет. Только если значения одинаковы, нужно проверять совпадение по буквам.

Что мы выигрываем при таком подходе? Казалось бы, ничего - ведь чтобы вычислить значение функции на слове в окошечке, все равно нужно прочесть все буквы этого слова. Так уж лучше их сразу сравнить с образцом. Тем не менее выигрыш возможен, и вот за счет чего. При сдвиге окошечка слово не меняется полностью, а лишь добавляется буква в конце и убирается в начале. Хорошо бы, чтобы по этим данным можно было рассчитать, как меняется функция.

10.6.1. Привести пример удобной для вычисления функции.

Решение. Заменим все буквы в слове и образце их номерами, представляющими собой целые числа. Тогда удобной функцией является сумма цифр. (При сдвиге окошечка нужно добавить новое число и вычесть пропавшее.)

Для каждой функции существуют слова, к которым она применима плохо. Зато другая функция в этом случае может работать хорошо. Возникает идея: надо запасти много функций и в начале работы алгоритма выбирать из них случайную. (Тогда враг, желающий подгадить нашему алгоритму, не будет знать, с какой именно функцией ему бороться.)

10.6.2. Привести пример семейства удобных функций.

Решение. Выберем некоторое число (желательно простое, смотри далее) и некоторый вычет по модулю . Каждое слово длины будем рассматривать как последовательность целых чисел (заменив буквы кодами). Эти числа будем рассматривать как коэффициенты многочлена степени и вычислим значение этого многочлена по модулю в точке . Это и будет одна из функций семейства (для каждой пары и получается, таким образом, своя функция). Сдвиг окошка на соответствует вычитанию старшего члена ( следует вычислить заранее), умножению на и добавлению свободного члена.

Следующее соображение говорит в пользу того, что совпадения не слишком вероятны. Пусть число фиксировано и к тому же простое, а и - два различных слова длины . Тогда им соответствуют различные многочлены (мы предполагаем, что коды всех букв различны - это возможно, если больше числа букв алфавита). Совпадение значений функции означает, что в точке эти два различных многочлена совпадают, то есть их разность обращается в . Разность есть многочлен степени и имеет не более корней. Таким образом, если много меньше , то случайному мало шансов попасть в неудачную точку.