| Россия, Пошатово |
Сортировка
4.5. Родственные сортировке задачи
4.5.1.
Какова минимально возможная сложность (число сравнений в наихудшем
случае) алгоритма отыскания самого тяжелого из  камней?
камней?
Решение. Очевидный алгоритм с инвариантом "найден
самый тяжелый камень среди первых  " требует
" требует  сравнений. Алгоритма меньшей сложности нет. Это вытекает из
следующего более сильного утверждения.
сравнений. Алгоритма меньшей сложности нет. Это вытекает из
следующего более сильного утверждения.
4.5.2.
Эксперт хочет убедить суд, что данный камень - самый
тяжелый среди  камней, сделав менее
камней, сделав менее  взвешиваний.
Доказать, что это невозможно. (Веса камней неизвестны
суду, но известны эксперту.)
взвешиваний.
Доказать, что это невозможно. (Веса камней неизвестны
суду, но известны эксперту.)
Решение. Изобразим камни точками, а взвешивания - линиями
между ними. Получим граф с  вершинами и менее чем
вершинами и менее чем  ребрами. Такой граф несвязен (добавление каждого следующего
ребра уменьшает число связных компонент не более чем
на
ребрами. Такой граф несвязен (добавление каждого следующего
ребра уменьшает число связных компонент не более чем
на  ). Поэтому суд ничего не знает относительно
соотношения весов камней в различных связных компонентах
и может допустить, что самый тяжелый камень - в любой из
них.
). Поэтому суд ничего не знает относительно
соотношения весов камней в различных связных компонентах
и может допустить, что самый тяжелый камень - в любой из
них.
Более простое объяснение: будем следить за тем, сколько
камней к данному моменту не "проиграли" (то есть не
оказались легче других). Вначале их  ; при каждом
взвешивании проигрывает только один камень, а если есть
двое не проигравших никому, любой из них может (с точки
зрения суда) оказаться самым тяжелым.
; при каждом
взвешивании проигрывает только один камень, а если есть
двое не проигравших никому, любой из них может (с точки
зрения суда) оказаться самым тяжелым.
Разница между этой задачей и предыдущей: в этой задаче мы
доказываем, что  взвешиваний не достаточно не только
для нахождения самого тяжелого, но даже для того, чтобы
убедиться, что данный камень является таковым - если
предположительный ответ известен. (В случае сортировки,
зная предположительный ответ, мы можем убедиться в его
правильности, сделав всего
взвешиваний не достаточно не только
для нахождения самого тяжелого, но даже для того, чтобы
убедиться, что данный камень является таковым - если
предположительный ответ известен. (В случае сортировки,
зная предположительный ответ, мы можем убедиться в его
правильности, сделав всего  сравнений - каждый
сравниваем со следующим по весу. Напомним, что сортировка
требует в худшем случае значительно больше сравнений.)
сравнений - каждый
сравниваем со следующим по весу. Напомним, что сортировка
требует в худшем случае значительно больше сравнений.)
4.5.3.
Доказать, что можно найти самый легкий и самый тяжелый из  камней (одновременно), сделав
камней (одновременно), сделав  взвешиваний.
взвешиваний.
Решение. Разобьем камни произвольным образом на  пар
и сравним камни в каждой паре (
пар
и сравним камни в каждой паре (  взвешиваний). Отложим
отдельно "победителей" (более тяжелых в своей паре)
и "проигравших" (более легких). Ясно, что самый
легкий камень надо искать среди проигравших (
взвешиваний). Отложим
отдельно "победителей" (более тяжелых в своей паре)
и "проигравших" (более легких). Ясно, что самый
легкий камень надо искать среди проигравших (  сравнений), а самый тяжелый - среди победителей (еще
сравнений), а самый тяжелый - среди победителей (еще  сравнений).
сравнений).
4.5.4.
Доказать, что не существует алгоритма, позволяющего
гарантированно найти самый легкий и самый тяжелый среди  камней (одновременно), сделав менее
камней (одновременно), сделав менее  взвешиваний.
взвешиваний.
Решение. Пусть такой алгоритм существует. Наблюдая за его
применением к какой-то группе из  камней, мы будем
следить за четырьмя параметрами. А именно, мы будем
смотреть, сколько камней
камней, мы будем
следить за четырьмя параметрами. А именно, мы будем
смотреть, сколько камней
(a) кому-то уже проиграли, а у кого-то уже выиграли;
(b) кому-то уже проиграли, но еще ни у кого не выиграли;
(c) у кого-то уже выиграли, но еще никому не проиграли;
(d) ни у кого не выиграли и никому не проиграли (то есть ни с кем не сравнивались).
(Напомним, что выигравшим в сравнении мы считаем более тяжелый камень.) Камни типа (a), очевидно, не могут уже оказаться ни самыми легкими, ни самыми тяжелыми, каковы бы ни были результаты дальнейших сравнений. Любой камень типа (b) имеет шанс оказаться самым легким (в самом деле, его можно произвольно облегчить, не меняя результатов уже выполненных сравнений), но уже не может быть самым тяжелым; для камней типа (c) наоборот. Наконец, любой камень типа (d) может быть и самым легким, и самым тяжелым.
Обозначим через 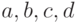 количества камней
в соответствующих категориях и проследим, как меняются эти
параметры при очередном сравнении (в зависимости от того,
камни какого типа сравниваются и с каким результатом).
количества камней
в соответствующих категориях и проследим, как меняются эти
параметры при очередном сравнении (в зависимости от того,
камни какого типа сравниваются и с каким результатом).
| сравнение | a | b | c | d | b+c+(3/2)d |
| a-a | 0 | 0 | 0 | 0 | 0 |
a>b a<b |
0 +1 |
0 -1 |
0 0 |
0 0 |
0 -1 |
a<c a>c |
0 +1 |
+1 0 |
0 -1 |
-1 0 |
0 -1 |
a>d a<d |
0 0 |
+1 0 |
0 +1 |
-1 -1 |
-1/2 -1/2 |
| b-b | +1 | -1 | 0 | 0 | -1 |
b<c b>c |
0 +2 |
0 -1 |
0 -1 |
0 0 |
0 -2 |
b<d b>d |
0 +1 |
0 0 |
+1 0 |
-1 -1 |
-1/2 -3/2 |
| c-c | +1 | 0 | -1 | 0 | -1 |
c<d c>d |
+1 0 |
0 +1 |
0 0 |
-1 -1 |
-3/2 -1/2 |
| d-d | 0 | +1 | +1 | -2 | -1 |
Последний столбец таблицы показывает, как меняется величина  (которую можно рассматривать
в качестве меры
"оставшейся работы": камень, про который не известно
ничего, с точки зрения этой меры в полтора раза сложнее
камня, для которого есть односторонняя оценка). Изначально
(которую можно рассматривать
в качестве меры
"оставшейся работы": камень, про который не известно
ничего, с точки зрения этой меры в полтора раза сложнее
камня, для которого есть односторонняя оценка). Изначально 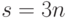 , а в конце
, а в конце  (про все камни, кроме двух,
известно, что они относятся к категории (a)). Из таблицы
видно, что при любом взвешивании есть "неудачный
исход", при котором
(про все камни, кроме двух,
известно, что они относятся к категории (a)). Из таблицы
видно, что при любом взвешивании есть "неудачный
исход", при котором  уменьшается не более чем на
единицу. Такие исходы действительно возможны (не
противоречат результатам предыдущих взвешиваний): при
сравнении
уменьшается не более чем на
единицу. Такие исходы действительно возможны (не
противоречат результатам предыдущих взвешиваний): при
сравнении  -камня и
-камня и  -камня может оказаться,
что
-камня может оказаться,
что  -камень тяжелее (его вес не ограничен сверху
предыдущими взвешиваниями), а при сравнении c участием
-камень тяжелее (его вес не ограничен сверху
предыдущими взвешиваниями), а при сравнении c участием  -камня результат может быть любым, поскольку про
-камня результат может быть любым, поскольку про  -камень ничего не известно. (Кроме того, можно
заметить, что один из исходов взвешивания невозможен, то
это взвешивание вообще излишне и его можно не делать.)
А если исходы всех взвешиваний неудачны, то уменьшение
-камень ничего не известно. (Кроме того, можно
заметить, что один из исходов взвешивания невозможен, то
это взвешивание вообще излишне и его можно не делать.)
А если исходы всех взвешиваний неудачны, то уменьшение  с
с  до
до  потребует как минимум
потребует как минимум  взвешиваний, что
и требовалось доказать.
взвешиваний, что
и требовалось доказать.
4.5.5.
Дано  различных по весу камней. Найти самый тяжелый
и второй по весу камни, сделав не более
различных по весу камней. Найти самый тяжелый
и второй по весу камни, сделав не более  взвешиваний (
взвешиваний ( 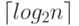 - наименьшее
целое
- наименьшее
целое  , при котором
, при котором  ).
).
Решение. Сначала найдем победителя (самый тяжелый камень),
а потом будем искать второй по весу. Ясно, что второго
можно искать лишь среди тех, кто проиграл лично победителю
(проигравшие кому-то еще легче сразу двух камней). Если
определять победителя в турнире по олимпийской системе (все
делятся на пары, проигравшие выбывают, потом снова делятся
на пары и так далее), то для 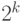 участников понадобится
участников понадобится  раундов, а для
раундов, а для  участников -
участников - 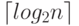 раундов. В каждой игре турнира выбывает один участник,
поэтому всего будет
раундов. В каждой игре турнира выбывает один участник,
поэтому всего будет  игр для определения победителя
и еще
игр для определения победителя
и еще  в турнире за второе место
среди проигравших победителю.
в турнире за второе место
среди проигравших победителю.
4.5.6.
Доказать, что никакой алгоритм нахождения самого тяжелого
и второго по весу среди  камней не может гарантированно
сделать это менее чем за
камней не может гарантированно
сделать это менее чем за  взвешиваний.
взвешиваний.
Решение. Пусть дан такой алгоритм. В каждый момент его
исполнения рассмотрим число 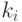 камней-участников,
проигравших не менее
камней-участников,
проигравших не менее  игр-сравнений. (Косвенные
проигрыши - если
игр-сравнений. (Косвенные
проигрыши - если  проиграл
проиграл  ,
а
,
а  проиграл
проиграл  , - не
учитываются.) Легко понять, что сумма
, - не
учитываются.) Легко понять, что сумма 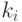 по всем
по всем  равна числу игр, так как после каждой игры одно из
равна числу игр, так как после каждой игры одно из 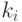 увеличивается на единицу.
увеличивается на единицу.
Поэтому достаточно показать, что каков бы ни был алгоритм,
при неудачных для него результатах игр будет выполнено
неравенство 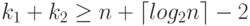 .
Будем называть " лидерами " тех участников, которые
еще никому не проиграли. В начале их
.
Будем называть " лидерами " тех участников, которые
еще никому не проиграли. В начале их  , а в конце
остается только один лидер (поскольку любой из лидеров
может быть победителем). Поэтому
, а в конце
остается только один лидер (поскольку любой из лидеров
может быть победителем). Поэтому  (все игроки,
кроме одного, кому-то проиграли). Объясним, как надо
выбирать результаты матчей, чтобы добиться неравенства
(все игроки,
кроме одного, кому-то проиграли). Объясним, как надо
выбирать результаты матчей, чтобы добиться неравенства  . Результат встречи двух не-лидеров может быть выбран любым. Если лидер
встречается с не-лидером, то выигрывает лидер. При
встрече двух лидеров выигрывает более опытный, то есть тот,
кто выиграл к этому моменту больше игр (при равенстве -
любой).
. Результат встречи двух не-лидеров может быть выбран любым. Если лидер
встречается с не-лидером, то выигрывает лидер. При
встрече двух лидеров выигрывает более опытный, то есть тот,
кто выиграл к этому моменту больше игр (при равенстве -
любой).
Чтобы доказать, что в этом случае выполнено искомое
неравенство на  , введем отношения подчинения, считая
при этом, что каждый игрок в любой момент игры подчинен
ровно одному лидеру. В начале каждый сам себе лидер
и подчинен только себе. При встрече лидера с не-лидером
(или двух не-лидеров) подчинение не меняется; при
встрече двух лидеров проигравший и все его подчиненные
переподчиняются выигравшему.
, введем отношения подчинения, считая
при этом, что каждый игрок в любой момент игры подчинен
ровно одному лидеру. В начале каждый сам себе лидер
и подчинен только себе. При встрече лидера с не-лидером
(или двух не-лидеров) подчинение не меняется; при
встрече двух лидеров проигравший и все его подчиненные
переподчиняются выигравшему.
Легко доказать по индукции, что если лидер выиграл  игр,
то группа его подчиненных (включая его самого) содержит не
более
игр,
то группа его подчиненных (включая его самого) содержит не
более 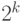 человек. Вначале
человек. Вначале 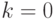 и в его группе только он сам. Если лидер выиграл
и в его группе только он сам. Если лидер выиграл  игр и побеждает лидера,
выигравшего не более
игр и побеждает лидера,
выигравшего не более  игр, то в каждой из групп не
более
игр, то в каждой из групп не
более 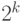 игроков, а в объединении не более
игроков, а в объединении не более  игроков.
игроков.
Следовательно, по окончании турнира лидер выиграл не менее 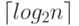 игр, поскольку в его группе
все
игр, поскольку в его группе
все  игроков. Все побежденные им, кроме второго по силе игрока,
проиграли еще кому-то (иначе почему мы уверены, что они
не вторые по силе?). Отсюда и получается требуемая оценка
на
игроков. Все побежденные им, кроме второго по силе игрока,
проиграли еще кому-то (иначе почему мы уверены, что они
не вторые по силе?). Отсюда и получается требуемая оценка
на  .
.
4.5.7. Доказать, что оценка предыдущей задачи остается в силе, если требуется найти лишь второй по весу камень, а самый тяжелый искать не обязательно.
Указание. Если по окончанию турнира определился второй по силе игрок, то он кому-то проиграл (откуда мы знаем иначе, что он не первый?), и тем самым известен и победитель.
4.5.8.
Дано  различных по весу камней и число
различных по весу камней и число  (от
(от  до
до  ). Требуется найти
). Требуется найти  -ый по весу камень, сделав
не более
-ый по весу камень, сделав
не более  взвешиваний, где
взвешиваний, где  - некоторая константа,
не зависящая от
- некоторая константа,
не зависящая от  и
и  .
.
Замечание. Сортировка позволяет сделать это за 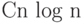 взвешиваний. Указание к этой (трудной) задаче приведено
в лекции про рекурсию.
взвешиваний. Указание к этой (трудной) задаче приведено
в лекции про рекурсию.
Следующая задача имеет неожиданно простое решение.
4.5.9.
Имеется  одинаковых на вид камней, некоторые из которых
на самом деле различны по весу. Имеется прибор, позволяющий
по двум камням определить, одинаковы они или различны (но
не говорящий, какой тяжелее). Известно, что среди этих
камней большинство (более
одинаковых на вид камней, некоторые из которых
на самом деле различны по весу. Имеется прибор, позволяющий
по двум камням определить, одинаковы они или различны (но
не говорящий, какой тяжелее). Известно, что среди этих
камней большинство (более 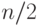 ) одинаковых. Сделав не
более
) одинаковых. Сделав не
более  взвешиваний, найти хотя бы один камень из этого
большинства. (Предостережение. Если два камня одинаковые,
это не гарантирует их принадлежности к большинству.)
взвешиваний, найти хотя бы один камень из этого
большинства. (Предостережение. Если два камня одинаковые,
это не гарантирует их принадлежности к большинству.)
Указание. Если найдены два различных камня, то их оба можно выбросить - хотя бы один из них плохой и большинство останется большинством.
Решение. Программа просматривает камни по очереди, храня в переменной i число просмотренных камней. (Считаем камни пронумерованными от 1 до n.) Помимо этого программа хранит номер "текущего кандидата" c и его "кратность" k. Смысл этих названий объясняется инвариантом (И):
Получаем такую программу:
k:=0; i:=0;
{(И)}
while i<>n do begin
| if k=0 then begin
| | k:=1; c:=i+1; i:=i+1;
| end else if (i+1-ый камень одинаков с c-ым) then begin
| | i:=i+1; k:=k+1;
| | {заменяем материальный камень идеальным}
| end else begin
| | i:=i+1; k:=k-1;
| | {выкидываем один материальный и один идеальный камень}
| end;
end;
искомым является c-ый каменьЗамечание. Поскольку во всех трех вариантах выбора стоит команда i:=i+1, ее можно вынести наружу.
Заметим также, что эта программа гарантирует отыскание наиболее частого камня, лишь если он составляет большинство.
Следующая задача не имеет на первый взгляд никакого отношения к сортировке.
4.5.10. Имеется квадратная таблица a[1..n,1..n]. Известно, что для некоторого i строка с номером i заполнена одними нулями, а столбец с номером i - одними единицами (за исключением их пересечения на диагонали, где стоит неизвестно что). Найти такое i (оно, очевидно, единственно). Число действий порядка n. (Заметим, что это существенно меньше числа элементов в таблице.)
Указание. Рассмотрите a[i][j] как результат "сравнения" i с j и вспомните, что самый тяжелый из n камней может быть найден за n сравнений. (Заметим, что таблица может не быть "транзитивной", но все равно при "сравнении" двух элементов один из них отпадает.)
