| Россия, Пошатово |
Сортировка
Первое действие (взятие элемента из первого отрезка) может производиться при одновременном выполнении двух условий:
(1) первый отрезок не кончился ( 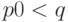 );
);
(2) второй отрезок кончился (  ) или не
кончился, но элемент в нем не меньше очередного элемента
первого отрезка [
) или не
кончился, но элемент в нем не меньше очередного элемента
первого отрезка [ 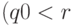 )
и (
)
и ( ![{x[p0+1]}\le{x[q0+1]}](/sites/default/files/tex_cache/afe5eee295cefdaeb1cc38ba38606beb.png) )].
)].
Аналогично для второго действия. Итак, получаем
p0 := p; q0 := q; s0 := p;
while (p0 <> q) or (q0 <> r) do begin
| if (p0 < q) and ((q0 = r) or ((q0 < r) and
| |(x[p0+1] <= x[q0+1]))) then begin
| | b [s0+1] := x [p0+1];
| | p0 := p0+1;
| | s0 := s0+1;
| end else begin
| | {(q0 < r) and ((p0 = q) or ((p0<q) and
| | (x[p0+1] >= x[q0+1])))}
| | b [s0+1] := x [q0+1];
| | q0 := q0 + 1;
| | s0 := s0 + 1;
| end;
end;(Если оба отрезка не кончены и первые невыбранные элементы в них равны, то допустимы оба действия; в программе выбрано первое.)
Остается лишь переписать результат слияния обратно в массив x. (Предупреждение. Если обратное копирование выполняется вне процедуры слияния, то не забудьте про последний отрезок.)
Программа имеет привычный дефект: обращение к несуществующим элементам массива при вычислении булевских выражений.
Решение 2 (сортировка деревом).
Нарисуем "полное двоичное дерево" - картинку, в которой снизу один кружок, из него выходят стрелки в два других, из каждого - в два других и так далее
Будем говорить, что стрелки ведут "от отцов к сыновьям": у каждого кружка два сына и один отец (если кружок не в самом верху или низу). Предположим для простоты, что количество подлежащих сортировке чисел есть степень двойки, и они могут заполнить один из рядов целиком. Запишем их туда. Затем заполним часть дерева под ними по правилу:
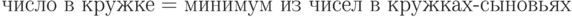
Изымем из сортируемого массива минимальный элемент. Для
этого его надо вначале найти. Это можно сделать, идя от
корня: от отца переходим к тому сыну, где записано то же
число. Изъяв минимальный элемент, заменим его символом  и скорректируем более низкие ярусы (для этого
надо снова пройти путь к корню). При этом считаем, что
и скорректируем более низкие ярусы (для этого
надо снова пройти путь к корню). При этом считаем, что  . Тогда в корне появится второй по
величине элемент, мы изымаем его, заменяя бесконечностью
и корректируя дерево. Так постепенно мы изымем все элементы
в порядке возрастания, пока в корне не останется
бесконечность.
. Тогда в корне появится второй по
величине элемент, мы изымаем его, заменяя бесконечностью
и корректируя дерево. Так постепенно мы изымем все элементы
в порядке возрастания, пока в корне не останется
бесконечность.
При записи этого алгоритма полезно нумеровать кружки
числами 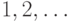 - при этом сыновьями кружка
номер n являются кружки 2n и
- при этом сыновьями кружка
номер n являются кружки 2n и 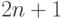 .
Подробное изложение этого алгоритма мы опустим, поскольку
мы изложим более эффективный вариант, не требующий
дополнительной памяти, кроме конечного числа переменных
(в дополнение к сортируемому массиву).
.
Подробное изложение этого алгоритма мы опустим, поскольку
мы изложим более эффективный вариант, не требующий
дополнительной памяти, кроме конечного числа переменных
(в дополнение к сортируемому массиву).
Мы будем записывать сортируемые числа во всех вершинах
дерева, а не только на верхнем уровне. Пусть ![{x[1]}\ldots{x[n]}](/sites/default/files/tex_cache/716647067f5d76102fd209a2c165c0db.png) - массив, подлежащий сортировке.
Вершинами дерева будут числа от 1 до n ; о числе x[i] мы будем говорить как о числе, стоящем
в вершине i. В процессе сортировки количество вершин
дерева будет сокращаться. Число вершин текущего дерева
будем хранить в переменной k. Таким образом, в процессе
работы алгоритма массив
- массив, подлежащий сортировке.
Вершинами дерева будут числа от 1 до n ; о числе x[i] мы будем говорить как о числе, стоящем
в вершине i. В процессе сортировки количество вершин
дерева будет сокращаться. Число вершин текущего дерева
будем хранить в переменной k. Таким образом, в процессе
работы алгоритма массив ![{x[1]}\ldots{x[n]}](/sites/default/files/tex_cache/716647067f5d76102fd209a2c165c0db.png) делится на
две части: в
делится на
две части: в ![{x[1]}\ldots{x[k]}](/sites/default/files/tex_cache/ed7ba99c83b01980f423a7ad385d6639.png) хранятся числа на
дереве, а в
хранятся числа на
дереве, а в ![{x[k+1]}\ldots{x[n]}](/sites/default/files/tex_cache/c1888c51e97ff4b796c9e4de2852bd52.png) хранится уже
отсортированная в порядке возрастания часть массива -
элементы, уже занявшие свое законное место
хранится уже
отсортированная в порядке возрастания часть массива -
элементы, уже занявшие свое законное место
На каждом шаге алгоритм будет изымать максимальный элемент дерева и помещать его в отсортированную часть, на освободившееся в результате сокращения дерева место.
Договоримся о терминологии. Вершинами дерева считаются
числа от 1 до текущего значения переменной k.
У каждой вершины s могут быть сыновья 2s
и 2s+1. Если оба этих числа больше k, то сыновей
нет; такая вершина называется листом. Если  , то вершина s имеет ровно одного сына
( 2s ).
, то вершина s имеет ровно одного сына
( 2s ).
Для каждого s из 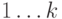 рассмотрим
"поддерево" с корнем в s: оно содержит
вершину s и всех ее потомков (сыновей, внуков и так
далее - до тех пор, пока мы не выйдем из отрезка
рассмотрим
"поддерево" с корнем в s: оно содержит
вершину s и всех ее потомков (сыновей, внуков и так
далее - до тех пор, пока мы не выйдем из отрезка 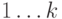 ). Вершину s будем называть регулярной, если стоящее в ней число -
максимальный элемент s -поддерева; s -поддерево
назовем регулярным, если все его вершины
регулярны. (В частности, любой лист образует регулярное одноэлементное поддерево.)
). Вершину s будем называть регулярной, если стоящее в ней число -
максимальный элемент s -поддерева; s -поддерево
назовем регулярным, если все его вершины
регулярны. (В частности, любой лист образует регулярное одноэлементное поддерево.)
Заметим, что истинность утверждения " s -поддерево регулярно" зависит не только от s, но от текущего значения k.
Схема алгоритма такова:
k:= n
... Сделать 1-поддерево регулярным;
{x[1],..,x[k] <= x[k+1] <=..<= x[n]; 1-поддерево регулярно,
в частности, x[1] - максимальный элемент среди x[1]..x[k]}
while k <> 1 do begin
| ... обменять местами x[1] и x[k];
| k := k - 1;
| {x[1]..x[k-1] <= x[k] <=...<= x[n]; 1-поддерево
| регулярно везде, кроме, возможно, самого корня }
| ... восстановить регулярность 1-поддерева всюду
end;В качестве вспомогательной процедуры нам понадобится процедура восстановления регулярности s -поддерева в корне. Вот она:
{s-поддерево регулярно везде, кроме, возможно, корня}
t := s;
{s-поддерево регулярно везде, кроме, возможно, вершины t}
while ((2*t+1 <= k) and (x[2*t+1] > x[t])) or
| ((2*t <= k) and (x[2*t] > x[t])) do begin
| if (2*t+1 <= k) and (x[2*t+1] >= x[2*t]) then begin
| | ... обменять x[t] и x[2*t+1];
| | t := 2*t + 1;
| end else begin
| | ... обменять x[t] и x[2*t];
| | t := 2*t;
| end;
end;