Сортировка

Чтобы убедиться в правильности этой процедуры, посмотрим на нее повнимательнее. Пусть в s -поддереве все вершины, кроме разве что вершины t, регулярны. Рассмотрим сыновей вершины t. Они регулярны, и потому содержат наибольшие числа в своих поддеревьях. Таким образом, на роль наибольшего числа в t -поддереве могут претендовать число в самой вершине t и числа в ее сыновьях. (В первом случае вершина t регулярна, и все в порядке.) В этих терминах цикл можно записать так:

while наибольшее число не в t, а в одном из сыновей do begin
| if оно в правом сыне then begin
| | поменять t с ее правым сыном; t:= правый сын
| end else begin {наибольшее число - в левом сыне}
| | поменять t с ее левым сыном; t:= левый сын
| end
end

После обмена вершина t становится регулярной (в нее попадает максимальное число t -поддерева). Не принявший участия в обмене сын остается регулярным, а принявший участие может и не быть регулярным. В остальных вершинах s -поддерева не изменились ни числа, ни поддеревья их потомков (разве что два элемента поддерева переставились), так что регулярность не нарушилась.

Эта же процедура может использоваться для того, чтобы сделать 1 -поддерево регулярным на начальной стадии сортировки:

k := n; u := n;
{все s-поддеревья с s>u регулярны }
while u<>0 do begin
| {u-поддерево регулярно везде, кроме разве что корня}
| ... восстановить регулярность u-поддерева в корне;
| u:=u-1;
end;

Теперь запишем процедуру сортировки на паскале (предполагая, что n - константа, x имеет тип ).

procedure sort (var x: arr);
| var u, k: integer;
| procedure exchange(i, j: integer);
| | var tmp: integer;
| | begin
| | tmp  := x[i];
| | x[i] := x[j];
| | x[j] := tmp;
| end;
| procedure restore (s: integer);
| | var t: integer;
| | begin
| | t:=s;
| | while ((2*t+1 <= k) and (x[2*t+1] > x[t])) or
| | |     ((2*t <= k) and (x[2*t] > x[t])) do begin
| | | if (2*t+1 <= k) and (x[2*t+1] >= x[2*t]) then begin
| | | | exchange (t, 2*t+1);
| | | | t := 2*t+1;
| | | end else begin
| | | | exchange (t, 2*t);
| | | | t := 2*t;
| | | end;
| | end;
| end;
begin
| k:=n;
| u:=n;
| while u <> 0 do begin
| | restore (u);
| | u := u - 1;
| end;
| while k <> 1 do begin
| | exchange (1, k);
| | k := k - 1;
| | restore (1);
| end;
end;

Несколько замечаний.

Метод, использованный при сортировке деревом, бывает полезным в других случаях. (См. в "Типы данных" (Типы данных) об очереди с приоритетами.)

Сортировка слиянием хороша тем, что она на требует, чтобы весь сортируемый массив помещался в оперативной памяти. Можно сначала отсортировать такие куски, которые помещаются в памяти (например, с помощью дерева), а затем сливать полученные файлы.

Еще один практически важный алгоритм сортировки (быстрая сортировка Хоара) таков: чтобы отсортировать массив, выберем случайный его элемент , и разобьем массив на три части: меньшие , равные и большие . (Эта задача приведена в "Переменные, выражения, присваивания" .) Теперь осталось отсортировать первую и третью части: это делается тем же способом. Время работы этого алгоритма - случайная величина; можно доказать, что в среднем он работает не больше 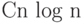. На практике - он один из самых быстрых. (Мы еще вернемся к нему, приведя его рекурсивную и нерекурсивную реализации.)

Наконец, отметим, что сортировка за время порядка 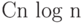может быть выполнена с помощью техники сбалансированных деревьев (см. "Представление множеств. Деревья. Сбалансированные деревья." ), однако программы тут сложнее и константа довольно велика.