| Россия, Пошатово |
Порождение комбинаторных объектов
2.7. Подсчет количеств
Иногда можно найти количество объектов с тем или иным
свойством, не перечисляя их. Классический пример: 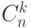 -
число всех
-
число всех  -элементных подмножеств
-элементных подмножеств  -элементного множества - можно найти, заполняя таблицу по формулам
-элементного множества - можно найти, заполняя таблицу по формулам
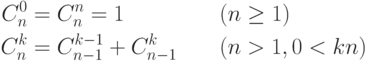
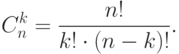
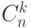 .)
.)Приведем другие примеры.
2.7.1.
(Число разбиений; предлагалась на Всесоюзной олимпиаде
по программированию 1988 года) Пусть  - число
разбиений целого положительного
- число
разбиений целого положительного  на целые положительные
слагаемые (без учета порядка,
на целые положительные
слагаемые (без учета порядка,  и
и  - одно и то
же
разбиение). При
- одно и то
же
разбиение). При 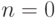 положим
положим 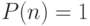 (единственное
разбиение не содержит слагаемых). Построить алгоритм
вычисления
(единственное
разбиение не содержит слагаемых). Построить алгоритм
вычисления  для заданного
для заданного  .
.
Решение. Можно доказать (это нетривиально) такую формулу
для  :
:

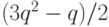 и
и 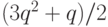 ; сумма конечна - мы
считаем, что
; сумма конечна - мы
считаем, что 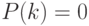 при
при  ).
).Однако и без ее использования можно придумать способ
вычисления  , который существенно эффективнее перебора
и подсчета всех разбиений.
, который существенно эффективнее перебора
и подсчета всех разбиений.
Обозначим через 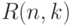 (для
(для  ,
,  ) число
разбиений
) число
разбиений  на целые положительные слагаемые, не
превосходящие
на целые положительные слагаемые, не
превосходящие  . (При этом
. (При этом 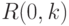 считаем
равным
считаем
равным  для всех
для всех  .) Очевидно,
.) Очевидно,  . Все
разбиения
. Все
разбиения  на слагаемые, не превосходящие
на слагаемые, не превосходящие  ,
разобьем
на группы в зависимости от максимального слагаемого
(обозначим его
,
разобьем
на группы в зависимости от максимального слагаемого
(обозначим его  ). Число
). Число 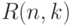 равно сумме (по
всем
равно сумме (по
всем  от
от  до
до  ) количеств разбиений
со слагаемыми
не больше
) количеств разбиений
со слагаемыми
не больше  и максимальным слагаемым, равным
и максимальным слагаемым, равным  .
А разбиения
.
А разбиения  на слагаемые не более
на слагаемые не более  с первым
слагаемым, равным
с первым
слагаемым, равным  , по существу представляют собой
разбиения
, по существу представляют собой
разбиения 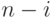 на слагаемые, не превосходящие
на слагаемые, не превосходящие  (при
(при 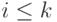 ). Так что
). Так что
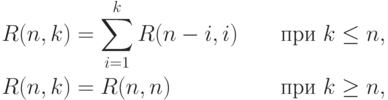
 .
.2.7.2.
(Счастливые билеты; предлагалась на Всесоюзной олимпиаде
по программированию 1989 года.) Последовательность из  цифр (каждая цифра от
цифр (каждая цифра от  до
до 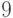 )
называется
счастливым билетом, если сумма первых
)
называется
счастливым билетом, если сумма первых  цифр равна сумме
последних
цифр равна сумме
последних  цифр. Найти число счастливых
последовательностей данной длины.
цифр. Найти число счастливых
последовательностей данной длины.
Решение. (Сообщено одним из участников олимпиады;
к сожалению, не могу указать фамилию, так как работы
проверялись зашифрованными.) Рассмотрим более общую задачу:
найти число последовательностей, где разница между суммой
первых  цифр и суммой последних
цифр и суммой последних  цифр
равна
цифр
равна  (
( 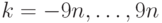 ). Пусть
). Пусть 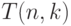 - число таких
последовательностей.
- число таких
последовательностей.
Разобьем множество таких последовательностей на классы
в зависимости от разницы между первой и последней цифрами.
Если эта разница равна  , то разница между суммами групп
из оставшихся
, то разница между суммами групп
из оставшихся  цифр равна
цифр равна  . Учитывая, что пар
цифр с разностью
. Учитывая, что пар
цифр с разностью  бывает
бывает  , получаем формулу
, получаем формулу
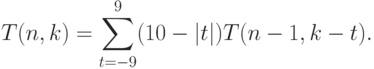
 может быть слишком велико.)
может быть слишком велико.)В некоторых случаях ответ удается получить в виде явной формулы.
2.7.3.
Доказать, что число Каталана (количество последовательностей длины  из
из  единиц
и
единиц
и  минус
единиц, в любом начальном отрезке которых не меньше единиц,
чем минус единиц) равно
минус
единиц, в любом начальном отрезке которых не меньше единиц,
чем минус единиц) равно 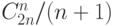 .
.
Указание. Число Каталана есть число ломаных, идущих из 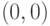 в
в 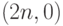 шагами
шагами  и
и 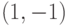 , не
опускающихся
в нижнюю полуплоскость, т.е. разность числа всех ломаных
(которое есть
, не
опускающихся
в нижнюю полуплоскость, т.е. разность числа всех ломаных
(которое есть 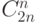 ) и числа ломаных, опускающихся
в нижнюю полуплоскость. Последние можно описать также как
ломаные, пересекающие прямую
) и числа ломаных, опускающихся
в нижнюю полуплоскость. Последние можно описать также как
ломаные, пересекающие прямую  . Отразив их кусок
справа от самой правой точки пересечения относительно
указанной прямой, мы установим взаимно однозначное
соответствие между ними и ломаными из
. Отразив их кусок
справа от самой правой точки пересечения относительно
указанной прямой, мы установим взаимно однозначное
соответствие между ними и ломаными из 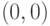 в
в 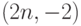 .
Остается проверить, что
.
Остается проверить, что  .
.
