Порождение комбинаторных объектов

2.6. Несколько замечаний

Посмотрим еще раз на использованные нами приемы. Вначале удавалось решить задачу по такой схеме: определяем порядок на подлежащих перечислению объектах и явно описываем процедуру перехода от данного объекта к следующему (в смысле этого порядка). В задаче о кодах Грея потребовалось хранить, помимо текущего объекта, и некоторую дополнительную информацию (направления стрелок). Наконец, в задаче о перечислении перестановок (на каждом шаге допустима одна транспозиция) мы применили такой прием: установили взаимно однозначное соответствие между перечисляемым множеством и другим, более просто устроенным. Таких соответствий в комбинаторике известно много. Мы приведем несколько задач, связанных с так называемыми " числами Каталана ".

2.6.1. Перечислить все последовательности длины 2n, составленные из n единиц и n минус единиц, у которых сумма любого начального отрезка неотрицательна, т.е. число минус единиц в нем не превосходит числа единиц. (Число таких последовательностей называют числом Каталана ; формулу для чисел Каталана см. в следующем разделе.)

Решение. Изображая единицу вектором (1,1), а минус единицу вектором (1,-1), можно сказать, что мы ищем пути из точки (0,0) в точку (n,0), не опускающиеся ниже оси абсцисс.

Будем перечислять последовательности в лексикографическом порядке, считая, что -1 предшествует 1. Первой последовательностью будет "пила"

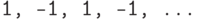
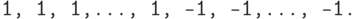
Как перейти от последовательности к следующей? До некоторого места они должны совпадать, а затем надо заменить -1 на 1. Место замены должно быть расположено как можно правее. Но заменять -1 на 1 можно только в том случае, если справа от нее есть единица (которую можно заменить на -1 ). После замены -1 на 1 мы приходим к такой задаче: фиксирован начальный кусок последовательности, надо найти минимальное продолжение. Ее решение: надо приписывать -1, если это не нарушит условия неотрицательности, а иначе приписывать 1. Получаем такую программу:

...
type array2n = array [1..2n] of integer;
...
procedure get_next (var a: array2n; var last: Boolean);
| {в a помещается следующая последовательность, если}
| {она есть (при этом last:=false), иначе last:=true}
| var k, i, sum: integer;
begin
| k:=2*n;
| {инвариант: в a[k+1..2n] только минус единицы}
| while a[k] = -1 do begin k:=k-1; end;
| {k - максимальное среди тех, для которых a[k]=1}
| while (k>0) and (a[k] = 1) do begin k:=k-1; end;
| {a[k] - самая правая -1, за которой есть 1;
|  если таких нет, то k=0}
| if k = 0 then begin
| | last := true;
| end else begin
| | last := false;
| | i:=0; sum:=0;
| | {sum = a[1]+...+a[i]}
| | while i< >k do begin
| | | i:=i+1; sum:= sum+a[i];
| | end;
| | {sum = a[1]+...+a[k], a[k]=-1}
| |  a[k]:= 1; sum:= sum+2;
| | {вплоть до a[k] все изменено, sum=a[1]+...+a[k]}
| | while k < > 2*n do begin
| | | k:=k+1;
| | | if sum > 0 then begin
| | | | a[k]:=-1
| | | end else begin
| | | | a[k]:=1;
| | | end;
| | | sum:= sum+a[k];
| | end;
| | {k=2n, sum=a[1]+...a[2n]=0}
| end;
end;

2.6.2. Перечислить все расстановки скобок в произведении n сомножителей. Порядок сомножителей не меняется, скобки полностью определяют порядок действий. Например, для n=4 есть 5 расстановок:

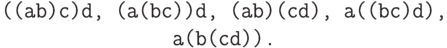
Указание. Каждому порядку действий соответствует последовательность команд стекового калькулятора, описанного в "Как обойтись без рекурсии"

2.6.3. На окружности задано 2n точек, пронумерованных от 1 до 2n. Перечислить все способы провести n непересекающихся хорд с вершинами в этих точках.

2.6.4. Перечислить все способы разрезать n -угольник на треугольники, проведя n-2 его диагонали.

(Мы вернемся к разрезанию многоугольника в разделе о динамическом программировании, "Как обойтись без рекурсии" )

Еще один класс задач на перечисление всех элементов заданного множества мы рассмотрим ниже, обсуждая метод поиска с возвратами (backtracking).