Рекуррентные сети на базе персептрона

Сеть RTRN

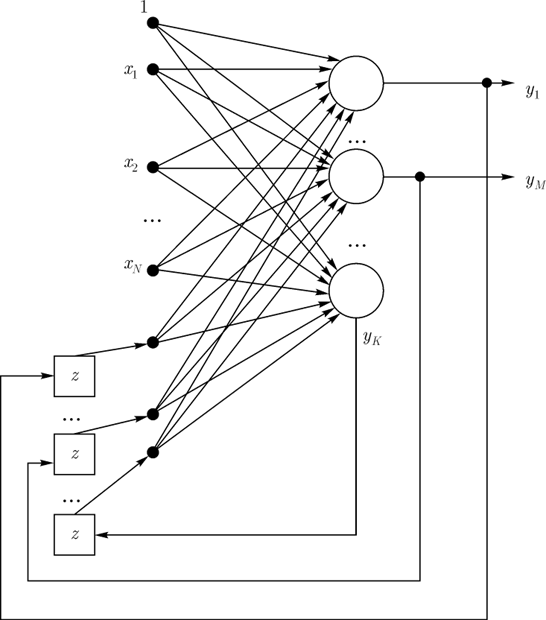
Среди рекуррентных сетей особого внимания заслуживает сеть типа RTRN (англ.: Real Time Recurrent Network), предложенная Р.Вильямсом и Д.Зипсером и предназначенная для обработки сигналов в реальном времени. Сеть RTRN - частный случай сети Эльмана.

увеличить изображение
Рис. 4. Структура сети RTRN

Обобщенная структура сети представлена на рис. 4. Сеть содержит входных узлов, скрытых нейронов и соответствующих им узлов контекстного слоя. Из скрытых нейронов только составляют выход сети. Обозначим взвешенную сумму -го нейрона скрытого слоя , а выход этого нейрона - . Вектор 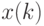и смещенный (задержанный) на один цикл вектор 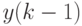образуют расширенный вектор активации 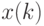, возбуждающий нейроны сети:

После описания входного вектора сети в момент можно определить состояние всех нейронов согласно зависимостям:

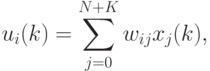( 2)

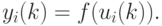( 3)

причем обозначает непрерывную функцию активации нейрона (как правило, сигмоидальную). На рис. 4 видно, что сеть RTRN представляет собой частный случай сети Эльмана, в которой веса выходного слоя постоянны и равны дельте Кронекера, т.е. 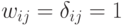для или для 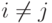. В этом случае можно применять алгоритм обучения Вильяма-Зипсера.

1. Выбрать случайные начальные значения весов сети, составляющих матрицу и равномерно распределенных в заданном интервале (обычно в диапазоне от до ).

2. Рассчитать состояние всех K нейронов для очередного момента 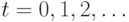с использованием формул (1) и (2). На этой основе можно определить входной вектор 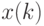, возбуждающий нейроны в момент .

3. Рассчитать значения

4. Уточнить значения весов по алгоритму наискорейшего спуска согласно формуле

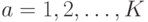для и .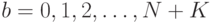

Шаги (2-4) повторять вплоть до стабилизации значений всех весов сети.