Рекуррентные сети на базе персептрона

Сеть Эльмана естественным образом предназначена для моделирования временных рядов. В частности, она решает задачу прогнозирования амплитуды сигнала на основе текущего значения входного сигнала и запомненных значений из предыдущего временного цикла. Задача прогноза временных рядов возникает в финансовой области: прогноз котировок товаров и ценных бумаг на бирже, курсов валют, показателей банковской деятельности. В экономике прогноз может быть связан, например, с анализом уровня производства в различных отраслях промышленности и сельского хозяйства, процента трудовой занятости населения, роста средней заработной платы. Проблема прогноза временных рядов возникает в многочисленных экологических задачах и самых разнообразных технических приложениях.

Для прогноза временных рядов могут применяться статистические методы. В этом случае должна быть построена динамическая модель данных (например, регрессионная модель) изучаемого явления. Для простейших задач такая модель может быть построена известными методами. Однако для практических задач, примеры которых приведены выше, построение подобной динамической модели представляет собой сложную аналитическую задачу. Эти приложения связаны обычно не со скалярными, а с векторными временными рядами. Например, в финансовой сфере прогноз котировок товара зависит от вектора динамических данных, которые включают цены открытия и закрытия торговой сессии, среднюю и максимальную цены торговой сессии, суммарный уровень заявок, валютные курсы и пр.

В том случае, когда адекватной математической модели изучаемых временных рядов не существует, удобным инструментом для решения задачи прогноза является нейросетевой экстраполятор динамических данных.

Задача прогноза векторного временного ряда ставится следующим образом:

• задана реализация временного ряда 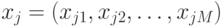, , 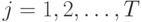на интервале времени с постоянным интервалом дискретности ;
• требуется построить оценку значения временного ряда (обычно одной его координаты) в момент времени 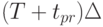, где 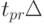- заданное время прогноза.

Из логических соображений или путем статистического анализа имеющейся реализации можно установить, сколько предшествующих значений относительно произвольного текущего момента времени 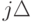определяюще связаны с прогнозируемым значением. Это означает, что если представить прогнозируемое значение 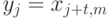-ой координаты вектора как функцию его предшествующих измерений:

то выбор значения устанавливает "память" экстраполятора. Значение определяет также входной вектор для нейронной сети, которая строится для решения задачи прогноза. Размерность этого вектора равна .

Таким образом, задача прогноза данных на нейронной сети сведена к задаче воспроизведения функции многих переменных , по данным обучающей выборки.