Орграфы

Эйлеровы и гамильтоновы орграфы

Связный орграф называется эйлеровым, если в нем существует замкнутая орцепь, содержащая каждую его дугу. Такая орцепь называется эйлеровой орцепью.

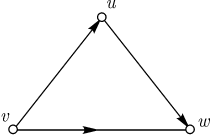
Например, граф, изображенный на рисунке, не является эйлеровым, хотя его основание — эйлеров граф.

Рис. 9.4.

Наша первая задача — найти условие, необходимое и достаточное для того, чтобы связный орграф был эйлеровым. Очевидно, что необходимым условием эйлеровости орграфа является его сильная связь. Если — вершина орграфа , то называют полустепенью исхода (обозначается — стрелка направлена от ) число дуг орграфа , имеющих вид 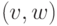. Аналогично, полустепенью захода (обозначается называется число дуг из вида . Отсюда сразу следует, что сумма полустепеней захода всех вершин орграфа равна сумме их полустепеней исхода, поскольку каждая дуга из участвует в каждой сумме ровно один раз. Будем называть этот результат орлемой о рукопожатиях!

Источником орграфа называют вершину, у которой полустепень захода равна нулю. Стоком орграфа называют вершину, у которой полустепень исхода равна нулю. Так, на (рис. 9.4) вершина является источником, а — стоком. Заметим, что эйлеров орграф, кроме тривиального орграфа, не содержащего дуг, не может иметь ни источников, ни стоков.

Теорема 9.2. Связный орграф является эйлеровым тогда и только тогда, если для каждой его вершины .

Теорема дается без доказательства, так как оно аналогично тем, которые даны в "Эйлеровы графы" .

Орграф называется гамильтоновым, если в нем существует орцикл, включающий каждую его вершину. Орграф, содержащий простую орцепь, проходящую через каждую вершину, называется полугамильтоновым. О гамильтоновых орграфах известно очень мало, к тому же некоторые теоремы о гамильтоновых графах, по-видимому, нелегко, если вообще возможно, обобщить на орграфы. Естественно спросить: обобщается ли на орграфы теорема Дирака? Одно такое обобщение принадлежит Гуйя-Ури. Доказательство этого утверждения значительно сложнее, чем доказательство теоремы Дирака, и выходит за рамки этого курса. Доказательство теоремы Гуйя-Ури можно найти в книге C.Berge, Graphs and hypergraphs, North-Holland, 1973, Р. 196.

Теорема (Гуйя-Ури, 1973) Пусть — сильно связный орграф, имеющий вершин. Если и для любой его вершины , то является гамильтоновым орграфом.

Кажется, что получать результаты в этом направлении не очень просто, поэтому ограничимся рассмотрением вопроса о том, какие типы орграфов являются гамильтоновыми. В этом аспекте широко известен один тип орграфов — турниры. Для них соответствующие результаты принимают наиболее простую форму.