| Россия |
Ординалы
Арифметика ординалов
Мы определили сумму
и произведение
линейно упорядоченных
множеств в
"лекции 7"
.
(Напомним, что
в  элементы
элементы  предшествуют
элементам
предшествуют
элементам  , а в
, а в  мы сначала сравниваем
мы сначала сравниваем  - компоненты пар, а в случае их
равенства-
- компоненты пар, а в случае их
равенства-  -
компоненты.)
-
компоненты.)
Легко проверить следующие свойства сложения:
- Сложение ассоциативно:
 .
. - Сложение не коммутативно: например,
 , но
, но 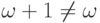 .
. - Очевидно,
 .
. - Сумма возрастает при росте
второго аргумента: если
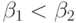 , то
, то  .
(В самом деле, пусть
.
(В самом деле, пусть 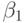 изоморфно начальному отрезку
в
изоморфно начальному отрезку
в 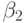 ,
отличному от всего
,
отличному от всего 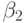 . Добавим к этому изоморфизму
тождественное отображение на
. Добавим к этому изоморфизму
тождественное отображение на  и получим изоморфизм
между
и получим изоморфизм
между  и начальным отрезком
в
и начальным отрезком
в  , отличным
от
, отличным
от  .)
.) - Сумма неубывает при росте первого аргумента: если
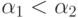 , то
, то 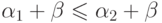 . (В самом деле,
. (В самом деле, 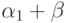 изоморфно
подмножеству в
изоморфно
подмножеству в 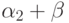 . Это подмножество не является
начальным отрезком, но мы можем воспользоваться
теоремой 37.)
. Это подмножество не является
начальным отрезком, но мы можем воспользоваться
теоремой 37.) - Определение суммы согласовано с обозначением
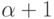 для
следующего
за
для
следующего
за  ординала. (Здесь
ординала. (Здесь  - порядковый тип
одноэлементного
множества.) Следующим за
- порядковый тип
одноэлементного
множества.) Следующим за 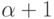 ординалом будет ординал
ординалом будет ординал 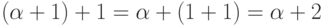 и т.д.
и т.д. - Если
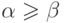 , то существует единственный
ординал
, то существует единственный
ординал 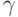 ,
для которого
,
для которого 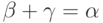 . (В самом деле,
. (В самом деле,  изоморфно
начальному отрезку в
изоморфно
начальному отрезку в  ; оставшаяся часть
; оставшаяся часть  и будет
искомым ординалом
и будет
искомым ординалом 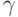 . Единственность следует из монотонности
сложения по второму аргументу.) Заметим, что эту операцию можно называть
" вычитание слева".
. Единственность следует из монотонности
сложения по второму аргументу.) Заметим, что эту операцию можно называть
" вычитание слева". - " Вычитание справа", напротив, возможно не всегда.
Пусть
 - некоторый ординал. Тогда уравнение
- некоторый ординал. Тогда уравнение 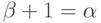 (относительно
(относительно  )
имеет решение тогда и только тогда, когда
)
имеет решение тогда и только тогда, когда  - непредельный
ординал,
(т.е. когда
- непредельный
ординал,
(т.е. когда  имеет наибольший элемент).
имеет наибольший элемент).
Определение суммы двух ординалов в силу ассоциативности можно
распространить на любое конечное число ординалов. Можно
определить и сумму  счетной
последовательности ординалов (элементы
счетной
последовательности ординалов (элементы 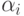 предшествуют
элементам
предшествуют
элементам 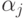 при
при 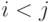 ; внутри
каждого
; внутри
каждого 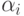 порядок прежний). Как легко проверить, это
множество действительно
будет вполне упорядоченным: чтобы найти минимальный элемент в его
подмножестве, рассмотрим компоненты, которые это подмножество
задевает, выберем из них компоненту с наименьшим номером и
воспользуемся ее полной упорядоченностью.
порядок прежний). Как легко проверить, это
множество действительно
будет вполне упорядоченным: чтобы найти минимальный элемент в его
подмножестве, рассмотрим компоненты, которые это подмножество
задевает, выберем из них компоненту с наименьшим номером и
воспользуемся ее полной упорядоченностью.
В этом построении можно заменить натуральные числа на элементы
произвольного вполне упорядоченного множества 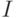 и определить
сумму
и определить
сумму 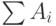 семейства вполне упорядоченных
множеств
семейства вполне упорядоченных
множеств  , индексированного элементами
, индексированного элементами 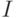 , как
порядковый
тип множества всех пар вида
, как
порядковый
тип множества всех пар вида 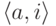 , для
которых
, для
которых 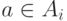 .
При сравнении пар сравниваются вторые компоненты, а в случае
равенства и первые (в соответствующем
.
При сравнении пар сравниваются вторые компоненты, а в случае
равенства и первые (в соответствующем  ). Если
все
). Если
все  изоморфны одному и тому же множеству
изоморфны одному и тому же множеству  , получаем уже известное
нам определение произведения
, получаем уже известное
нам определение произведения 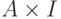 .
.
Теперь перейдем к умножению ординалов.
- Умножение ассоциативно:
 . (В самом деле, в обоих случаях
по существу получается множество троек; тройки сравниваются
справа налево, пока не обнаружится различие.)
. (В самом деле, в обоих случаях
по существу получается множество троек; тройки сравниваются
справа налево, пока не обнаружится различие.) - Умножение не коммутативно: например,
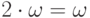 ,
в то время как
,
в то время как  .
. - Очевидно,
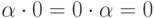 и
и 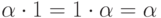 .
. - Выполняется одно из свойств дистрибутивности:
 (непосредственно следует из определения). Симметричное свойство
выполнено не всегда:
(непосредственно следует из определения). Симметричное свойство
выполнено не всегда: 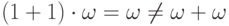 .
. - Произведение строго возрастает при увеличении второго
множителя, если первый не равен
 . (Для разнообразия выведем
это из ранее доказанных свойств: если
. (Для разнообразия выведем
это из ранее доказанных свойств: если  , то
, то 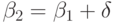 , так что
, так что 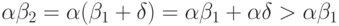 .)
.) - Произведение не убывает при возрастании первого множителя.
(В самом деле, если
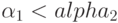 , то
, то 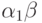 изоморфно
подмножеству
изоморфно
подмножеству  . Это подмножество не является
начальным отрезком, но можно сослаться на
теорему 37.)
. Это подмножество не является
начальным отрезком, но можно сослаться на
теорему 37.) - Любой ординал, меньший
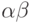 , однозначно
представим в виде
, однозначно
представим в виде 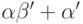 , где
, где 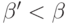 и
и 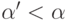 .
.(В самом деле, пусть множества
 и
и  упорядочены по типам
упорядочены по типам  и
и  . Тогда
. Тогда  упорядочено по типу
упорядочено по типу 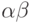 . Всякий ординал, меньший
. Всякий ординал, меньший 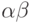 , есть начальный отрезок в
, есть начальный отрезок в  ,
ограниченный некоторым элементом
,
ограниченный некоторым элементом 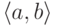 .
Начальный отрезок
.
Начальный отрезок 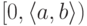 состоит из пар, у
которых второй член меньше
состоит из пар, у
которых второй член меньше  , а также из пар, у которых второй
член равен
, а также из пар, у которых второй
член равен  , а первый меньше
, а первый меньше  . Отсюда следует, что
этот
начальный отрезок изоморфен
. Отсюда следует, что
этот
начальный отрезок изоморфен 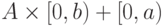 , так что
остается положить
, так что
остается положить  и
и  . Теперь
проверим однозначность. Пусть
. Теперь
проверим однозначность. Пусть 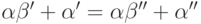 . Если
. Если 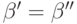 , то можно воспользоваться однозначностью левого
вычитания и получить, что
, то можно воспользоваться однозначностью левого
вычитания и получить, что 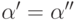 . Остается
проверить, что
. Остается
проверить, что 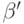 не может быть, скажем, меньше
не может быть, скажем, меньше  .
В этом случае
.
В этом случае 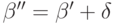 , и сокращая
, и сокращая 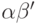 слева, получим, что
слева, получим, что 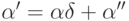 , что
невозможно, так как левая часть меньше
, что
невозможно, так как левая часть меньше  , а правая часть
больше или равна
, а правая часть
больше или равна  .)
.) - Аналогичное " деление с остатком" возможно и для
любых ординалов. Пусть
 . Тогда любой
ординал
. Тогда любой
ординал 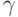 можно разделить с остатком на
можно разделить с остатком на  , то есть представить в
виде
, то есть представить в
виде 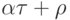 , где
, где 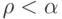 , и притом
единственным образом.
, и притом
единственным образом.(В самом деле, существование следует из предыдущего утверждения, надо только взять достаточно большое
 , чтобы
, чтобы 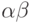 было больше
было больше 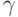 , скажем,
, скажем, 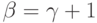 .
Единственность
доказывается так же, как и в предыдущем пункте.)
.
Единственность
доказывается так же, как и в предыдущем пункте.) - Повторяя деление с остатком на
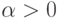 , можно построить
позиционную систему счисления для
ординалов: всякий ординал,
меньший
, можно построить
позиционную систему счисления для
ординалов: всякий ординал,
меньший  (здесь
(здесь  - натуральное число),
однозначно представим в виде
- натуральное число),
однозначно представим в виде 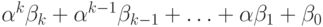 , где
, где 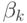 ,
,  ,
, 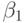 ,
, 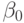 - ординалы, меньшие
- ординалы, меньшие  .
.
127. Для каких ординалов 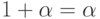 ?
?
128. Для каких ординалов  ?
?
129. Какие ординалы представимы в виде 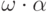 ?
?
130. Докажите, что 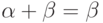 тогда и только тогда,
когда
тогда и только тогда,
когда 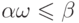 (здесь
(здесь  и
и  -
ординалы).
-
ординалы).
131. Докажите, что если  для некоторых
ординалов
для некоторых
ординалов  и
и  , то найдется такой
ординал
, то найдется такой
ординал 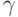 и
такие натуральные числа
и
такие натуральные числа  и
и  , что
, что  и
и 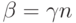 .
.
132. Определим операцию "замены основания" с  на
на  .
Чтобы применить эту операцию к натуральному числу
.
Чтобы применить эту операцию к натуральному числу  , надо
записать
, надо
записать  в
в  - ичной системе счисления, а затем
прочесть эту запись в
- ичной системе счисления, а затем
прочесть эту запись в  - ичной системе. (Очевидно, число при этом
возрастет, если оно было больше или равно
- ичной системе. (Очевидно, число при этом
возрастет, если оно было больше или равно  .)
Возьмем произвольное число
.)
Возьмем произвольное число  и будет выполнять над ним
такие операции: замена основания с
и будет выполнять над ним
такие операции: замена основания с 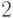 на
на 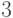 -
вычитание единицы -
замена основания с
-
вычитание единицы -
замена основания с 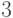 на
на 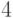 - вычитание единицы -
замена основания с
- вычитание единицы -
замена основания с 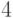 на
на 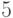 - вычитание единицы -
...
Докажите, что рано или поздно мы получим нуль и вычесть единицу
не удастся. (Указание: замените все основания на ординал
- вычитание единицы -
...
Докажите, что рано или поздно мы получим нуль и вычесть единицу
не удастся. (Указание: замените все основания на ординал 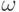 ;
получится убывающая последовательность ординалов.)
;
получится убывающая последовательность ординалов.)
