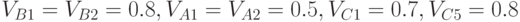|
"Тогда как задать возбуждение рецепторов, если инспектор точно установил, что скорость автомобиля при наезде на пешехода была равна 114 км/час? Вопрос по расчёту скорости и сумме достоверности: этот математический (приведенный выше в виде контекста из материала лекции 1, страницы 3) метод справедлив к скоростным показателям выходящим за рамки диапазона 100-120. |
Построение обученных логических нейронных сетей
Построение нейросети "под задачу"
Мы построили нейросеть – с экзотическими (с точки зрения невропатолога) конъюнкторами и дизъюнкторами.
Предположим теперь, что все нейроны одинаковы, реализуют одну функцию активации, а веса и пороги реализуют равные и общие возможности.
Введем функцию активации без ограничения по величине возбуждения, но не отрицательную (отрицательное значение разности примем нулевым):
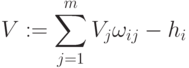
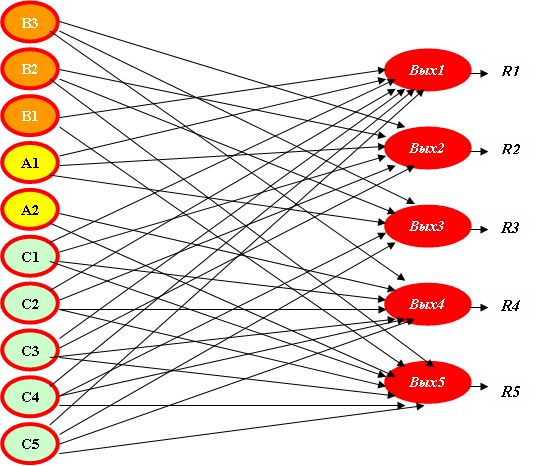
Положим 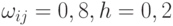 . Сеть представлена на рис.2.13.
. Сеть представлена на рис.2.13.
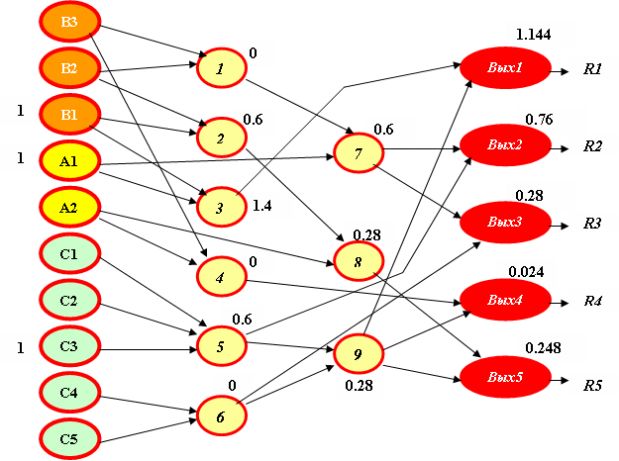
Подадим на вход, например, ситуацию {A1, B1, C3}, требующую решения R1. Величины возбуждений нейронов показаны на рисунке.
На основе расчетов по полученной сети составим табл. 2.3.1, отображающую правильную (!) работу сети при получении различных решений. При этом связи, предыстория которых определена дизъюнкторами, требуют проверки не более чем одного "представителя": в рассмотренном примере получаем тот же результат, если вместо С3 положим С1 или С2.
Анализируя первые восемь строк таблицы, соответствующие достоверным ситуациям, видим, что, по крайней мере, максимум возбуждения определяется устойчиво верно. Так что верификация нейронной сети прошла успешно, и сеть заслуживает доверия.
Рассмотрим ту же неопределенную ситуацию, показанную на рис.2.12. Она отражена в последней строке таблицы. Близка ли она более всего ситуации, когда Петя направился к Аполлинарии и надо принимать решение R5? Ситуация с Васей, устремившимся туда же, дает примерно тот же ответ.
Отметим, что по убыванию величин возбуждения нейронов выходного слоя, вновь полученный результат полностью совпадает с полученным по "схемотехнической" сети (рис.2.12), так что и величина средней прибыли, по-видимому, будет близка найденной ранее.
Переход к однослойной нейронной сети
Однако не проще было бы применять способ построения нейросети, близкий к табличному? Что, если каждую ситуацию непосредственно "замкнуть" на соответствующее решение, избежав сложной путаницы промежуточных слоев нейронов и не рассчитывая множества вариантов для нахождения максимального возбуждения, и распределения возбуждения на выходном слое?
Очень часто на практике так и поступают. Поэтому широкое распространение получили так называемые однослойные сети. Построим такую сеть и для нашего примера (рис.2.14).
Возьмем ту же функцию активации, с теми же параметрами и рассчитаем те же примеры, отображенные в табл. 2.3.1. Составим для них табл. 2.3.2.
Данная нейросеть также оказывает предпочтение решению R5, хотя порядок убывания величин возбуждения выходного слоя отличен от ранее полученного. Предпочтительность решений R2 и R3 меняется местами.