|
"Тогда как задать возбуждение рецепторов, если инспектор точно установил, что скорость автомобиля при наезде на пешехода была равна 114 км/час? Вопрос по расчёту скорости и сумме достоверности: этот математический (приведенный выше в виде контекста из материала лекции 1, страницы 3) метод справедлив к скоростным показателям выходящим за рамки диапазона 100-120. |
Система принятия решений на основе математической логики событий
Исчерпывающее множество событий
Ученые объяснения большей частью производят то впечатление, что бывшее ясно и понятно становится темно и запутанно.
Следующие ниже построения не могут не затронуть смысловых особенностей высказываний о событиях. Кроме чисто формальных свойств высказываний, выражающихся в их истинности или ложности, невозможно полностью абстрагироваться от содержательной сути или от контекста, в котором они звучат.
Определение 3.1. Исчерпывающее множество событий (ИМС) образуют те события, совокупность высказываний о которых покрывает весь возможный смысловой диапазон проявления объекта высказывания, и каждая допустимая ситуация характеризуется тем, что значение ИСТИНА (1) может принимать единственное высказывание из этой совокупности. (Значение 0 могут принимать все высказывания.)
Рассмотрим примеры.
1) В состав редколлегии входят трое: Иванов, Петров, Сидоров. Тогда провозглашение фамилий этих фигурантов определяет исчерпывающее множество событий при выдвижении единственного представителя коллектива в президиум собрания.
2) Наказуемое превышение скорости автомобиля делится на диапазоны: до 10%, от 10% до 20%, свыше 20%. Однако, если в регламентирующем документе заданы только диапазоны до 10% и от 10% до 100% (а что далее?), то это не будет соответствовать исчерпывающему множеству событий . Такие нестрогие определения возможного диапазона ситуаций являются причиной юридической казуистики, требующей дальнейшего исследования прецедента.
Итак, ИМС, которому соответствует множество высказываний 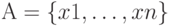 , характеризуется тем, что при соответствующих обстоятельствах одно и только одно высказывание из этого множества может принимать значение 1. Это и определяется операцией ИСКЛЮЧАЮЩЕЕ ИЛИ, которую будем обозначать .
, характеризуется тем, что при соответствующих обстоятельствах одно и только одно высказывание из этого множества может принимать значение 1. Это и определяется операцией ИСКЛЮЧАЮЩЕЕ ИЛИ, которую будем обозначать .
Очевидны главные свойства высказываний о событиях из ИМС:
 |
( 3.1) |
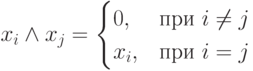 |
( 3.2) |
Дерево логических возможностей. Факторное пространство событий
Для строгого логического мышления, исключающего неопределенность, приходится оперировать не отдельными событиями и даже не исчерпывающими множествами таких событий (высказываниями о них), а композициями таких множеств. Между событиями, принадлежащими различным множествам, возможна зависимость, порождающая сложные высказывания. Да и сами ИМС могут определяться и инициироваться обстоятельствами, обусловленными событиями из других ИМС. Связи между ИМС, образующие сложные высказывания, отображаются деревом логических возможностей .
Рассмотрим пример.
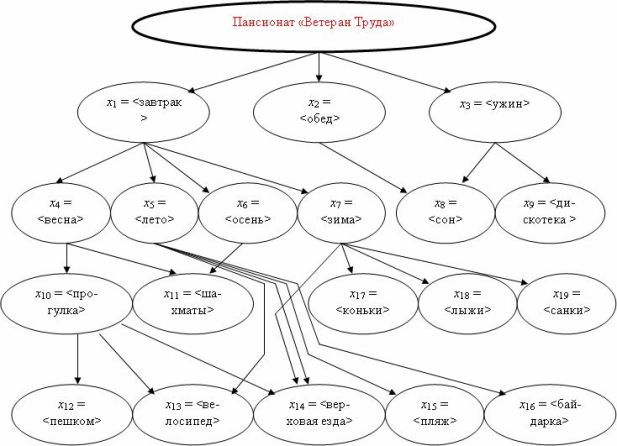
Пансионат для ветеранов труда обеспечивает постояльцам активный отдых круглый год. Представим схемой (рис.3.1) распорядок дня отдыхающих. Такая схема и определит дерево логических возможностей.
Уровни ветвления могут формироваться разными способами. Например, первый уровень можно сформировать на основе времен года и т.д. Однако в порядке рекомендации можно следовать правилу: события располагаются на более низких уровнях по сравнению с теми уровнями, которые занимают события, от которых зависят данные события.
Бабушка пишет внуку: "Зимой я после завтрака катаюсь на лошади, и летом я после завтрака катаюсь на лошади, а также весной после завтрака прогулка бывает на лошади". …Что-то ей не нравится, и она строит схему своего составного высказывания: 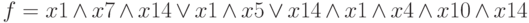 . Несколько поразмыслив, бабушка использует вынесение за скобку:
. Несколько поразмыслив, бабушка использует вынесение за скобку:  . Тогда окончательный текст сообщения принимает вид: "После завтрака я катаюсь на лошади летом или зимой, а также, бывает, и весной, — вместо прогулки". Как же бабушка определила форму того логического выражения, — функции, отображающей все возможные варианты, и даже пути, ведущие к свершению интересующего события?
. Тогда окончательный текст сообщения принимает вид: "После завтрака я катаюсь на лошади летом или зимой, а также, бывает, и весной, — вместо прогулки". Как же бабушка определила форму того логического выражения, — функции, отображающей все возможные варианты, и даже пути, ведущие к свершению интересующего события?
Ответ следующий: необходимо на каждом пути в дереве логических возможностей , ведущем к заданному событию, построить конъюнкцию событий, образующих этот путь. Затем все такие конъюнкции объединить операцией дизъюнкции. Поскольку используются только исчерпывающие множества событий , очевидно, что эта дизъюнкция выполняется с помощью операции 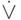 , т.е. ИСКЛЮЧАЮЩЕЕ ИЛИ (хотя можно пользоваться значком
, т.е. ИСКЛЮЧАЮЩЕЕ ИЛИ (хотя можно пользоваться значком 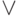 , опираясь на действительный, "физический" смысл возможных событий).
, опираясь на действительный, "физический" смысл возможных событий).
Полученная таким способом функция вызывает естественное желание быть подвергнутой дистрибутивному преобразованию — "вынесению за скобки".
Отметим, что в результате такого способа построения искомая функция принимает вид, при котором каждая используемая переменная-высказывание входит не более одного раза.
Например, функция, отображающая такое событие в жизни бабушки, как езда на велосипеде, имеет вид: 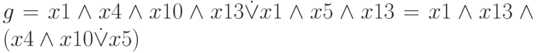 .
.
Однако далее будет показано, что не всегда единственного вхождения переменных можно добиться с помощью дистрибутивных преобразований. Иногда требуются дополнительные действия для его осуществления.
Определение 3.2. Совокупность всех исследуемых в данном контексте событий, т.е. множество – объединение всех рассматриваемых ИМС, образует факторное пространство событий .
Как и ранее, точку факторного пространства (ситуацию) будем обозначать 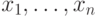 .
.
Итак, показана возможность построения логических функций на основе высказываний о событиях из факторного пространства. Как видно из примера, факторное пространство событий отображается ветвящейся структурой на основе отдельных исчерпывающих множеств событий , входящих в его состав. Тогда подмножества, состоящие из таких ИМС, тоже являются факторными подпространствами, которые в некотором контексте можно исследовать отдельно.
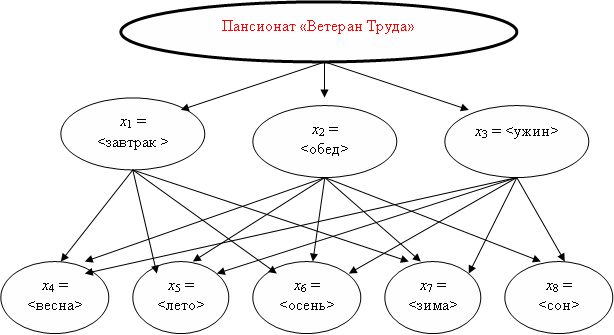
Например, можно отдельно исследовать факторное подпространство, сформированное на основе первых двух уровней ветвления (рис.3.2) в приведенном на рис.3.1 дереве логических возможностей . Это может быть необходимо при планировании финансовых расходов пансионата на питание.
Можно, в соответствии с поставленной задачей (в контексте исследований), формировать другие факторные пространства событий . Например, планирование использования спортивного инвентаря по времени года приводит к целесообразности факторного пространства, структура которого показана на рис.3.3.
Система принятия решений
Для некоторой логической функции f от переменных из факторного пространства событий воспользуемся операцией следования (импликации) и сформируем логическое выражение вида
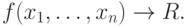 |
( 3.3) |
Здесь f следует рассматривать как выражение, определяющее условие, сложившуюся ситуацию, посылку, а R – высказывание, которое рассматривается как следствие: правило поведения, значение векторной функции, указание к действию и т.д. Таким образом, возможно формирование связей вида "посылка – следствие", "если … то". При этом функция f задается на множестве ситуаций и указывает на то, что, если на некоторой ситуации она принимает значение 1 (ИСТИНА), то такое же значение принимает высказывание R, являясь руководством к действию, к принятию определенного решения.
Подобно (3.3), можно описать множество логических выражений, определяющих стройную систему управления или принятия решений в соответствии со складывающейся ситуацией в факторном пространстве событий :
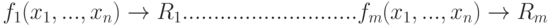 |
( 3.4) |
Определение 3.3. Система логических выражений вида (3.4), заданная на факторном пространстве (подпространстве) событий, обладающая полнотой и непротиворечивостью, называется системой принятия решений (СПР).
Поясним важность свойств, указанных в определении.
То, что система функций  является полной, означает, что любая точка факторного пространства событий входит в область задания хотя бы одной из этих функций. Непротиворечивость означает, что по каждой ситуации одна и только одна из этих функций принимает значение 1, приводящее к истинности соответствующего высказывания – решения. Однако отметим, что, в действительности, на основе смыслового содержания задачи, по каждой или некоторой ситуации может быть известно более одного правильного решения, приводящего к успешным действиям. В таком случае высказывания об этих решениях могут быть объединены операцией ИЛИ, что приводит к приведенному выше предположению о непротиворечивости.
является полной, означает, что любая точка факторного пространства событий входит в область задания хотя бы одной из этих функций. Непротиворечивость означает, что по каждой ситуации одна и только одна из этих функций принимает значение 1, приводящее к истинности соответствующего высказывания – решения. Однако отметим, что, в действительности, на основе смыслового содержания задачи, по каждой или некоторой ситуации может быть известно более одного правильного решения, приводящего к успешным действиям. В таком случае высказывания об этих решениях могут быть объединены операцией ИЛИ, что приводит к приведенному выше предположению о непротиворечивости.
Приведем теорему, которая дает обоснование общего вида логического описания любой системы принятия решений – того вида, к которому на пути упрощения задачи рекомендуется приводить описание СПР для нейросетевой реализации.
Теорема. Любая логическая функция, входящая в состав описания системы принятия решений, может быть приведена к дизъюнкции конъюнкций высказываний о событиях.
Доказательство. Из основ математической логики (в частности, - теории булевых функций) известно, что каждая такая функция может быть представлена дизъюнктивной нормальной формой. Однако в ней, наряду с переменными, участвуют их отрицания. Ориентируясь на применение исчерпывающих множеств событий , воспользуемся (3.1) для выражения таких отрицаний. "Раскроем скобки", вновь выделив конъюнкции, объединенные операциями дизъюнкции. Упростим эти конъюнкции с помощью (3.2). Получим форму, объявленную в теореме. Теорема доказана.
Данная теорема объясняет, почему в последующих примерах преимущественно принимается именно объявленная форма описания СПР, или легко сводящаяся к ней, а отрицания событий не рассматриваются.
Пусть известная нам бабушка планирует занятия физкультурой и спортом во все времена года по времени дня: после завтрака, после обеда и после ужина. Объединяя высказывания по принципу "если … то" и пользуясь обозначениями на рис.3.1, она формирует систему принятия решений, которой, не полагаясь на память, намерена строго следовать, добившись согласия администрации.
Система имеет вид:
 |
( 3.5) |
Планируя пешую прогулку, бабушка первоначально получила следующее выражение:

Однако выше не напрасно обращается внимание на целесообразность однократного вхождения переменных в подобное выражение. (Ведь далее, при переходе к функции активации нейрона, возможно неоднократное суммирование одних и тех же переменных.) Выражение, полученное первоначально, с помощью эквивалентных преобразований привести к такому виду не удается. Тогда бабушка решает разбить это выражение на два подобных, сформировав получение одного и того же решения ("размножив" решение) на основе двух условий. Это и послужило появлению в (3.5) двух выражений, определяющих одно решение  .
.
Легко убедиться, что все возможные ситуации факторного пространства событий охвачены, что демонстрирует полную ясность действий бабушки.
Системы принятия решений могут образовывать сложные иерархические структуры. В этом случае необходимо, чтобы высказывания-решения 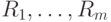 отображали события, образующие ИМС.
отображали события, образующие ИМС.