|
"Тогда как задать возбуждение рецепторов, если инспектор точно установил, что скорость автомобиля при наезде на пешехода была равна 114 км/час? Вопрос по расчёту скорости и сумме достоверности: этот математический (приведенный выше в виде контекста из материала лекции 1, страницы 3) метод справедлив к скоростным показателям выходящим за рамки диапазона 100-120. |
Нейросетевые технологии в экономике и бизнесе
Мониторинг банковской системы
Структура нейросети и способы обучения
Щ о е в… (Углубленно.) Пускай теперь наука трудится, а человек около нее как на курорте.
Логические функции, лежащие в основе мониторинга , преимущественно основаны на конъюнкции логических значений, утверждающих определенные диапазоны изменения параметров или показателей банков. В общем виде такая логическая функция имела бы вид 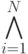 , значение i-го показателя банка принадлежит диапазону
, значение i-го показателя банка принадлежит диапазону ![[a, b]}\to](/sites/default/files/tex_cache/dc46334ac2c6d21500af55bc07cf1d6a.png) указатель значения рейтинга
указатель значения рейтинга
Известны показатели:
- собственный капитал;
- сальдированные активы;
- ликвидные активы;
- обязательства до востребования;
- вклады населения;
- коэффициент ликвидности;
- бюджетные средства.
Фантазируя, мы могли бы развить эту систему показателей:
- объем инвестиций в бурно развивающуюся экономику;
- объем прибыли;
- прошлый рейтинг и значение миграции;
- отчисления в фонд поддержки науки и образования;
- налоговые отчисления;
- отчисления в пенсионный фонд;
- отчисления в благотворительный и культурный фонд;
- участие в программах ЮНЕСКО и т.д.
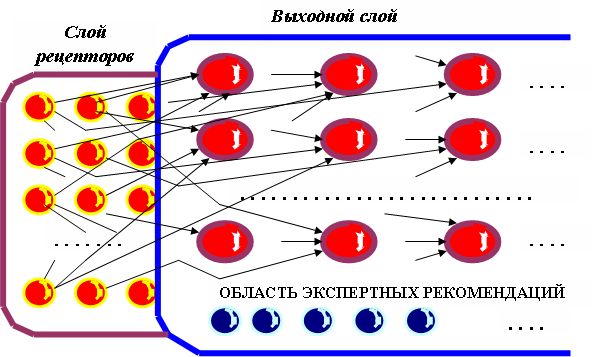
Такой простой вид логической функции, при переходе в область действительных переменных, говорит о достаточности однослойной нейросети (рис.8.1), содержащей входной слой рецепторов и выходной слой, указывающий на результаты мониторинга .
При создании входного слоя необходимо учитывать не только текущие показатели, но и, например, динамику изменения рейтинга — рейтинга за прошлые периоды времени.
Выходной слой должен отражать не только рейтинг, но и экспертные рекомендации, а также другие решения и выводы.
Целесообразен простейший вид обучения (т.е. построения базы знаний, какой является наша сеть), определяемый концепцией создания нейросети "под задачу". Он заключается в непосредственном введении связей в совершенной нейросети оператором-исследователем "вручную" — от рецепторов к нейронам выходного слоя в соответствии с причинно-следственными связями. Тем самым, сеть создается уже обученной.
Тогда функция активации должна быть тоже простейшей и основанной на суммировании величин возбуждения на входе нейрона, умноженных на вес связи:


Вес  связей все же целесообразен (по сравнению с грубым заданием всех весов равными единице) в связи с возможным желанием оператора или эксперта в разной степени учитывать влияние различных показателей.
связей все же целесообразен (по сравнению с грубым заданием всех весов равными единице) в связи с возможным желанием оператора или эксперта в разной степени учитывать влияние различных показателей.
Порог h отсекает заведомо "плохие" выводы, упрощая дальнейшую обработку (например, нахождение среднего). Коэффициент приведения k обусловлен следующим. Максимальное значение V может достигать n — числа показателей. Чтобы свести значение рейтинга в некоторый приемлемый диапазон, например, в [0, 1], значения возбуждения надо преобразовать в этот диапазон, положив, например,  Кроме того, этим коэффициентом, как и весами, можно регулировать значимость факторов в соответствии со сделанным ниже замечанием.
Кроме того, этим коэффициентом, как и весами, можно регулировать значимость факторов в соответствии со сделанным ниже замечанием.
Принятые выше решения позволяют оперативно вносить изменения и уточнения оператором-экспертом-пользователем, развивать сеть, вводя новые факторы и учитывая опыт. Для этого оператору достаточно, "топнув" мышкой, выделить рецептор, а затем — нейрон выходного слоя, и связь установлена! Осталось только на основе предположения (ясновидения), осуществляя эксперимент, приблизительно установить вес введенной связи из диапазона (0, 1].
И здесь мы должны сделать Очень Важное Замечание (ОВЗ), распространенное на весь материал и адресованное очень внимательному читателю.
Ранее, рассматривая обучение, мы четко классифицировали исходные эталонные ситуации, считая достоверность каждого компонента равной единице. Проводя затем трассировку, мы, прокладывая динамические пути возбуждения, также полагали веса связей равными единице (или некоторому максимальному постоянному значению). Но ведь можно сразу дать возможность (дать дополнительную степень свободы) учителю учитывать факторы в той степени, с теми весами, с которыми он пожелает! То есть допустить, что разные факторы в разной степени влияют на результат, и такое влияние заложить на этапе обучения принудительно!
Например, известно, что накануне войны население в огромном количестве закупает мыло, спички и соль. Значит, следя за этим фактором, можно предсказывать скорое наступление войны. Создавая нейросеть для предсказания исторических или социальных событий, следует выделить один или несколько рецепторов, возбуждение которых соответствует разному уровню закупок мыла, соли и спичек одновременно. Возбуждение этих рецепторов должно передаваться, влиять (наряду с другими факторами) на степень возбуждения нейрона выходного слоя, "отвечающего" за заявление: "Скоро война!".
Однако мы вправе считать, что интенсивная закупка мыла, спичек и соли необходимое, но не такое уж достаточное условие наступления войны. Оно может свидетельствовать, например, о бурном возрождении туризма в районе Главного Кавказского Хребта. В словах "не такое уж" заключается смысл нечеткой логики [10], позволяющей учитывать не непреложность влияния события, не булеву переменную "да — нет", а некоторое промежуточное, неопределенное, взвешенное предположение типа "влияет, но не так уж прямо, что уж обязательно…". Поэтому мы сразу можем связи (все или некоторые), исходящие из данного (данных) рецептора, положить равными некоторой предполагаемой величине, меньшей единицы, корректируемой впоследствии, отражающей влияние возбуждения этого рецептора на вывод. В этом и состоит главный смысл коэффициента k.
Таким образом, одновременная закупка мыла, соли и спичек будет учитываться дважды: уровень закупки будет отображаться в уровне возбуждения соответствующих этим уровням рецепторов, а степень влияния этой закупки на вывод "Скоро война!" будет учитываться с помощью весов синапсических связей.
Согласитесь, что при построении одноуровневых сетей такой учет напрашивается, реализуется предельно просто, что мы и рекомендуем делать.
Конец ОВЗ.
Структура экрана рецепторов
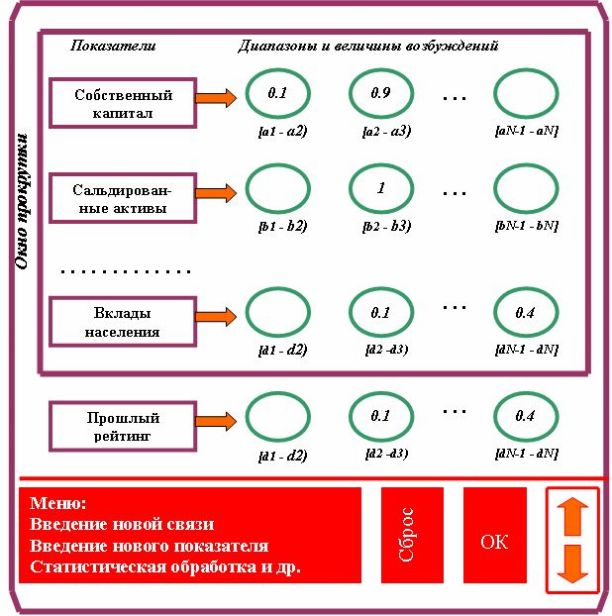
Экран рецепторов (проект) показан на рис.8.2.
Основную часть его составляет "окно прокрутки", через которое можно просматривать и задавать состояние рецепторного слоя, несомненно, не способного поместиться на статическом экране.
В "окне прокрутки" указаны показатели и их оценочные значения (в диапазоне [0, 1]), задаваемые соответствующим рецепторам. Эти значения — вероятностные, по достоверности, интуитивные, экспертные. Они могут предполагать охват нескольких рецепторов. Например, оценка того, что собственный капитал составляет не то 24, не то 34, не то 42 тыс. у. е., но скорее, все-таки, 24, может привести к приблизительной оценке задаваемых величин возбуждения, равных 0,6, 0,2 и 0,2 соответственно рецепторов, "отвечающих" за диапазоны (20 - 25], (30 - 35], (40 - 45].
На экране отображены статически (без прокрутки) задаваемые показатели, такие, как рейтинг в результате прошлых измерений, выборочные "прошлые" показатели, а также показатели политической, социальной и экономической конъюнктуры. (Их обилие и развитие могут все-таки потребовать прокрутки.)
Должно быть отображено управление прокруткой, а также меню основных действий. Эти действия следующие:
- переход на экран выходного слоя;
- статистическая обработка результатов (предполагает переход к выходному экрану);
- введение новой связи;
- введение нового рецептора;
- введение нового нейрона выходного слоя (предполагает переключение экранов);
- введение нового показателя и т.д.
Структура экрана выходного слоя
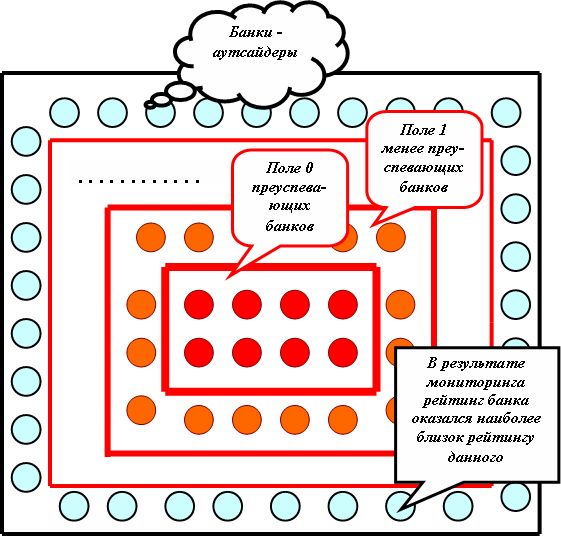
Экран выходного слоя (рис.8.3) может отображать систему концентрических (вложенных) прямоугольников или других плоских фигур, отражающих распространение рейтинга по убыванию. В центре экрана яркими точками отражены самые преуспевающие банки или предполагаемые идеальные образы. Каждый элемент экрана жестко закреплен за нейроном выходного слоя. В результате мониторинга может максимально возбудиться нейрон, соответствующий эталону, что должно быть понятно отображено. Однако, скорее всего, высветится точка экрана, не совпадающая ни с каким эталоном и являющаяся промежуточной или усредненной. (Эталоны, см. ниже, отображают все категории банков, отнюдь не только самые преуспевающие.)
Несомненно, должно быть отображено меню, позволяющее выполнить операции усредненной оценки рейтинга, демонстрации категории преуспевания, выдачи сигналов предупреждения, текстов-заключений, рекомендуемых стратегий развития, сохранения данных для дальнейшего развития и т.д.
Однако экран, связанный с декартовой системой координат, затрудняет интерполяцию (в частности, необходимую при решении настоящей задачи). А именно, найденная на основе усреднения координата двух точек, принадлежащих некоторому, предположим, - низкому, рейтингу, может оказаться между этими точками и принадлежать области высокого рейтинга.
Для облегчения интерполяции целесообразно в качестве рабочей системы использовать сферическую систему координат Or  , в которой
, в которой 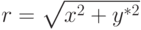 ,
,  . Общий центр О этих двух систем координат является центром экрана. Тогда области одинакового рейтинга ограничены сферическими окружностями.
. Общий центр О этих двух систем координат является центром экрана. Тогда области одинакового рейтинга ограничены сферическими окружностями.
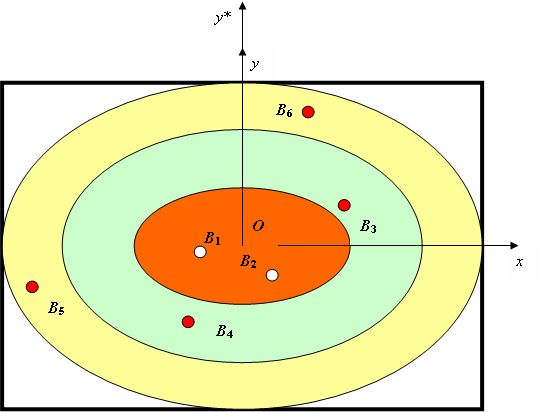
Для согласования с размером экрана компьютера необходимо произвести преобразование координаты y*: y = y*k, где k < 1 – отношение сторон экрана. Это приведет к "сплющиванию" изображения областей рейтинга согласно требованиям эстетики и удобств восприятия (рис.8.4).
Например, пусть в декартовой системе координат известны и распределены по областям одного рейтинга точки, соответствующие банкам:Т 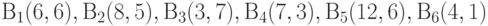 .
.
Тогда в сферической системе координат эти же точки определяются как: 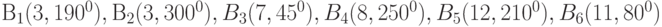 .
.
Обучение нейросети
Для обучения нейросети на основе экспертных оценок должны быть известны диапазоны допустимых параметров, которые позволяют считать банк идеально преуспевающим, имеющим максимальный рейтинг. Фиксируя несколько точек, координаты которых (множества значений параметров) удовлетворяют допустимым значениям рейтинга для известных или предполагаемых (с учетом возможных вариантов) банков, мы можем получить несколько идеальных представителей. Соответствующие им нейроны, т.е. элементы экрана выходного слоя, можно выделять произвольно, рассредоточивая по области экрана. Желательно, чтобы эталоны с большим рейтингом "располагались" ближе к центру.
Далее переходят к подобному же заполнению охватывающего прямоугольника, на основе следующей рейтинговой категории и т.д. — до банков-аутсайдеров .
Для проведения подобной работы эксперты должны предварительно сформировать таблицу, подобную табл. 8.1.
| Показатели | Рейтинг | Эталоны | |||
|---|---|---|---|---|---|
 |
 |
…… | 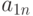 |
1 | Идеальные банки |
 |
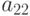 |
…… | 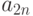 |
0,9 | |
| … | … | …… | … | … | |
 |
 |
…… | 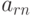 |
0,86 | |
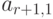 |
 |
…… | 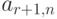 |
0,85 | Менее преуспевающие банки |
| … | … | …… | … | … | |
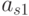 |
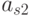 |
…… | 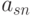 |
0,8 | |
| … | … | …… | … | … | |
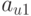 |
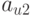 |
…… |  |
0,7 | Банки-аутсайдеры |
| … | … | …… | … | … | |
 |
 |
…… |  |
0,1 | |
При нейронах, отображающих банки, запоминаются (и записываются при символах этих нейронов на экране) рейтинги, как говорилось выше.