Нейросетевые самообучающиеся и адаптивные системы управления

Нейросетевой метод "бесформульных" вычислений

"...Не упрямься! что тебе стоит? плюнь да поцелуй у злод... (тьфу!) поцелуй у него ручку".

А.С. Пушкин, "Капитанская дочка"

Логическая нейронная сеть, имитирующая "бесформульное" ассоциативное мышление, строится на основе логического описания системы, которую в самом общем применении следует назвать системой принятия решений. Ее основой является воспроизведение записей вида "если ... то", "посылка ... следствие".

На основе аналога "электронной" схемы функционирования системы производится переход от булевых переменных, задающих события, к действительным, соответствующим достоверности высказываний о событиях. Таким образом, исходная информация формируется на основе достоверности принадлежности данных объектам, значениям или диапазонам значений. Логические элементы заменяются образами нейронов – простейшими пороговыми функциями активации. Применение аппарата логических функций и исчерпывающих множеств событий позволяет, без рассмотрения обратных связей, максимально упрощать структуру логических нейронных сетей, сводя их к однослойным. В этом случае логическая нейронная сеть представляет базу знаний, отображающую опыт. В ней известные ситуации непосредственно связаны с известными принимаемыми по ним решениями или предварительно найденными результатами сложных расчетов. Опыт учитывается в режиме обучения – построения нейросети. В рабочем режиме возникшая ситуация приближенно отображается возбуждением рецепторов, и по характеру возбуждения нейронов выходного слоя, в результате выполнения ими функции активации, принимается решение – наиболее близкое или усредненное. Так осуществляется ассоциативное мышление.

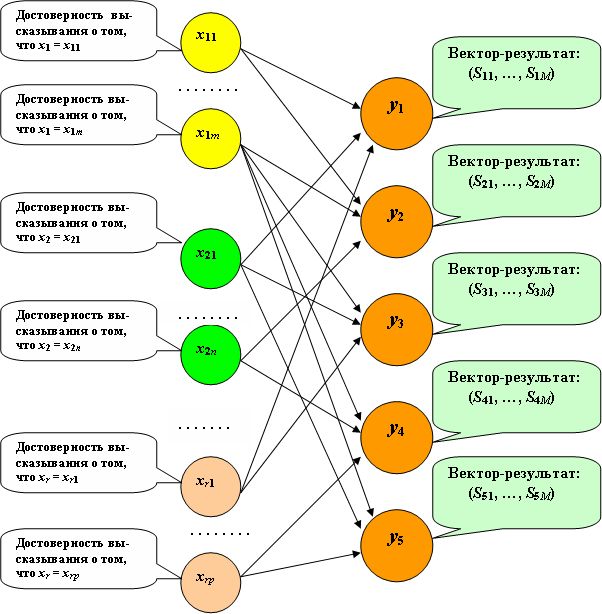
Рассмотрим пример сложных вычислений, близких к табличным, но легко допускающих любую размерность исходных данных и результатов, а также дополнение и модификацию (рис.6.1).

По компонентам вектора-ситуации, предъявленного в рабочем режиме, формируется возбуждение рецепторов. Простейший способ такого возбуждения заключается в распределении "единицы" обратно пропорционально разности значения компоненты с ближайшими двумя ограничивающими точками. При значительной неопределенности исходных данных можно имитировать нормальный закон распределения достоверности их принадлежности нескольким значениям, за которыми закреплены рецепторы. Далее считается значение функции активации всех нейронов выходного слоя. Простейшая, рекомендуемая для этих целей, функция активации имеет вид:

Здесь 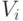– величина возбуждения рецептора, подаваемая на вход нейрона.

Максимально возбудившийся нейрон указывает на решение. Однако если компоненты решения целые или действительные числа, то может быть произведено усреднение этой компоненты по нескольким возбудившимся нейронам.

Рис. 6.1. Логическая нейронная сеть для расчета векторной функции векторной переменной

Рецепторы могут закрепляться не только между значениями переменных, для которых известен опыт, но и между диапазонами их изменения.

Универсальность такого приема реализации ассоциативного мышления в силу тривиальности на логическом (но не на биологическом) уровне, по-видимому, служит основой управления и мышления в живой природе. Этот принцип лежит в основе моделирования для различных приложений. Привлекательность метода логических нейронных сетей – в достижении высокой реальной производительности при решении задач (по сравнению с традиционными "алгоритмическими" методами), возможность широкого распараллеливания (подобно мозговым процессам), возможность создания простого и универсального интерфейса пользователя, допускающего широкие возможности эксперимента, модификации, смены специализации и т.д.

Самообучение на основе ситуационного управления

Для трудно формализуемых задач управления или для увеличения производительности вычислительных средств известно т.н. ситуационное управление , предложенное Д.А. Поспеловым [4]. Оно заключается в том, что для каждого значения вектора, описывающего сложившуюся ситуацию, известно значение вектора, описывающего то решение, которое следует принять. Если все ситуации отразить невозможно, должно быть задано правило интерполяции (аналог интерполяции, обобщенная интерполяция).

Таким образом, наметилась та же схема вычислений, что была рассмотрена выше. На основе известных решений, соответствующих складывающимся ситуациям, формируется база знаний (БЗ). Работа с БЗ требует механизмов ассоциативной выборки, в результате которой осуществляется необходимая интерполяция. Такие механизмы наилучшим образом реализуются с помощью логической нейронной сети. База знаний оказывается записанной в том же виде, что показан на рис.6.2.

Как же реализовать самообучение БЗ, то есть ее обучение и развитие на основе опыта эксплуатации?

увеличить изображение
Рис. 6.2. Схема самообучения с моделью

Далеко не всегда будет правильным развитие базы знаний только на основе ошибочного принятия решений. "Учение на ошибках" может привести к трагедии (или к частному срыву процесса управления), особенно на этапе обучения системы. Обучение системы целесообразно проводить на достаточно точной модели, максимально использующей точный расчет компонент решения. Применение модели используется не только на специально предусмотренном этапе обучения системы, но и вне реального цикла управления, т.е. когда система работает в режиме дежурства, параллельно с функциональным контролем. Алгоритм ее работы представлен на рис.6.2.

Нейросетевое воплощение

Мы уже построили нейросеть для важной задачи принятия решений и вручили ее Заказчику — дяде Рамзаю. Однако, задумчиво глядя в синее небо под бодрящий рокот набегающей волны теплого течения Гольфстрим, мы не можем прогнать мыслей об обобщениях, вариациях и применениях…

Итак, еще раз тщательно проследим принцип динамического совмещения процесса обучения системы управления с процессом выдачи решений, изложенный выше, и установим в схеме на рис.6.2 целесообразность, место и способ использования нейронной сети как основного реального средства искусственного интеллекта. Прежде всего, мы понимаем, что основным естественным и целесообразным местом применения нейросети здесь является база знаний. Нам только надо позаботиться о том, чтобы "крутились" там не численные значения информации, а вес этой информации или ее достоверность. То есть, не сама информация должна обрабатываться нейросетью, а ее логический эквивалент. Ведь мы поняли, что принцип искусственного интеллекта направлен на параллельную обработку логических высказываний, а вовсе не ориентирован напрямую на числовую обработку информации, как это делается при решении некоторых "нейроподобных" задач при использовании нейросети в роли спецпроцессора.

увеличить изображение
Рис. 6.3. Управляющая система с нейросетью

Пусть нейросеть в роли базы знаний имеет текущий вид, представленный на рис.6.3.

Нейроны-рецепторы оказались закрепленными за значениями элементов входного вектора. Это значит, что в режиме обучения (или в процессе динамической корректировки) установилось соответствие на основе положения: "величина возбуждения данного p-го нейрона входного слоя принимает значение достоверности того, что .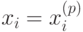

Как мы ранее делали, при обучении мы полагаем эту достоверность равной единице, а в процессе распознавания может быть что угодно, даже не удовлетворяющее свойству полноты событий.

Таким образом, "показывая" сети на этапе обучения различные эталоны, методом трассировки или непосредственно мы можем добиться установления соответствия вида 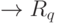, наполнив тем самым базу знаний. Каждое решение 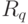при этом тоже указывает на определенное значение вектора — результата 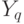, компоненты которого суть управляющие воздействия системы.То есть, нейроны 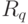фактически закрепляются за ситуациями, по которым мы знаем векторы характеристик или значений параметров принимаемых решений — векторы значений управляющих воздействий.

Как в этом случае задавать информацию на рецепторном слое при поступлении вектора-запроса ?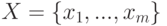

Для каждого 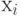найдем две "близкие" точки и 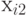, которые представлены рецепторами нейросети и для которых выполняется соотношение . Зададим возбуждение рецептора Вход равным значению 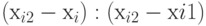, а возбуждение рецептора Вход 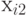– равным значению .

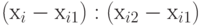Однако все или некоторые нейроны-рецепторы могут закрепляться не за конкретными значениями входных параметров, а за диапазонами их изменения, если это соответствует необходимой точности управления.

Для нахождения значений управляющих воздействий в зависимости от значений исходных данных может быть использовано моделирование, наряду с экспериментом или с экспертными оценками. Таким образом, модель, эксперимент или эксперт играют роль учителя. (Мы ранее уже высказали сомнение насчет существования и действенности "чистого" самообучения .) Отметим, что модель может быть основана на алгоритмах расчетного характера. Однако модель может, в свою очередь, воплощать методы искусственного интеллекта, реализуя, например, метод "проб и ошибок".

Первоначально обученная таким образом нейросеть может быть уже использована в рабочем режиме (распознавания) и в режиме совместной работы с моделью. При этом мы понимаем, что нейросеть обучена недостаточно, и, подобно пристрелке реперов "в свободное от работы" время, мы пытаемся с помощью модели испытать и, в случае необходимости, дополнить знания нейросети.

Для этого модель случайно или направленно — по обоснованному плану - "выбрасывает" некоторую ситуацию, характеризующуюся значением компонент входного вектора Х. По каждой компоненте определяется вес или достоверность того, что ее значение совпадает с подмножеством значений этой компоненты, представленных входным слоем нейросети, или с диапазонами значений этой компоненты.

Например, сеть "знает" реакцию на значение (опустим индекс) x = 2, x = 5, x = 6. Модель выбросила значение х = 5,7. Это может означать необходимость формирования значений возбуждения 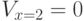, , 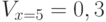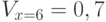. Здесь индексы возбуждений указывают нейроны входного слоя, закрепленные за данным значением параметра. Так делается по всем компонентам входного слоя.

Не следует забывать, что в общем случае управляющая информация может выдаваться данными разных типов, не обязательно действительными или целыми. В частности, это может быть текстовая информация, содержащая исторические аналогии, рекомендации, инструкции или даже алгоритмы действий. Поэтому, если какие-то компоненты управляющего вектора допускают усреднение по нескольким векторам, на которые указывают нейроны со своими величинами возбуждения, то с помощью этих величин может быть произведено усреднение значений этих компонент. Например, пусть, "пройдя" по сети, возбуждение рецепторов привело к преодолению порога возбуждения нейронов выходного слоя R5 (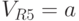), R7 (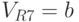), R12 (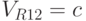). При этом нейрону R5 соответствует вектор численных (!) значений управляющих воздействий 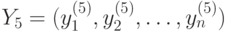, нейрону R7 — вектор 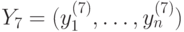, нейрону R12 - вектор 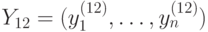. Тогда предполагаемый ответ нейросети находится:

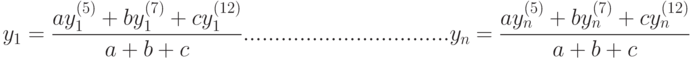
Подставляем данное решение в модель и устанавливаем, удовлетворяет ли нас оно, — например, по величине промаха. Если удовлетворяет, мы делаем положительный вывод об обученности нейросети и продолжаем ее испытание по другим исходным данным. Если нет, — сеть необходимо "доучить", продемонстрировав самый высокий логический уровень обратной связи.

Для этого мы должны ввести в действие новые рецепторы, закрепив их за теми значениями исходных данных или их диапазонами, которые ранее не были представлены. Например, нам придется закрепить рецептор за значением х = 5,7 или за небольшим диапазоном, включающим это значение. Для сохранения однозначности решений этот диапазон необходимо исключить из других диапазонов, с которыми возникло пересечение.

Далее, мы должны выделить нейрон выходного слоя и закрепить его за соответствующим правильным решением, которое мы должны получить с помощью модели.

Далее, мы должны выполнить трассировку (или ввести связи "вручную") для того, чтобы задание нового эталона с единичной достоверностью исходных данных приводило к максимальному возбуждению выделенного нейрона выходного слоя, ответственного за получение правильного решения.

Таким образом, сеть может обучаться до тех пор, пока не перестанет давать "сбоев". А поскольку в вероятностном аспекте это вряд ли возможно, то в таком режиме она должна работать в течение всего жизненного цикла, реализуя известную пословицу "Век живи — век учись…".

Здесь наглядно представлена замечательная возможность нейросети: табличная аппроксимация функции многих переменных, снабженная процедурой интерполяции (экстраполяции) для нахождения по произвольному значению вектора-аргумента приближенного значения векторной функции. При этом входной вектор возбуждений рецепторов преобразуется в максимальное или усредненное значение возбуждения нейронов выходного слоя, указывающего на соответствующее значение вектора-функции. Так что практически столь простым способом мы построили постоянно уточняющуюся аппроксимацию векторной функции от векторного аргумента!

Логическая нейронная сеть может быть построена и обучена так, чтобы заданное значение 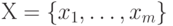приводило к максимальному (или усредненному) значению возбуждения нейрона выходного слоя, указывающего соответствующее значение 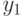, к максимальному (или усредненному) значению возбуждения другого нейрона выходного слоя, указывающего на значение 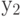и т.д. Выходной слой оказывается разбит на области, каждая из которых закреплена за своим параметром 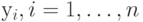. Тогда полученное преобразование можно условно записать 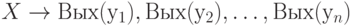, как это показано на рис.6.4.

Рис. 6.4. Раздельное нахождение управляющих параметров с помощью нейросети

Следует обратить внимание не только на высокую производительность такого рода самообучающихся систем в рабочем режиме, но и на их адаптивность, развиваемость, живучесть и т.д.