|
"Тогда как задать возбуждение рецепторов, если инспектор точно установил, что скорость автомобиля при наезде на пешехода была равна 114 км/час? Вопрос по расчёту скорости и сумме достоверности: этот математический (приведенный выше в виде контекста из материала лекции 1, страницы 3) метод справедлив к скоростным показателям выходящим за рамки диапазона 100-120. |
Нейросетевые модели пошаговой оптимизации, маршрутизации и тактических игр
Логическая нейронная сеть — средство пошагового принятия решений
Будут игры беспредельные,
В упоительности цельные…
Задачи пошаговой оптимизации составляют широкий класс задач исследования операций. Это — многочисленные задачи нахождения оптимальных стратегий управления, таких, как вывод космического объекта в заданную точку, минимизация длины пути следования в транспортной сети и др.
Однако высокая сложность задач указанного типа выдвигает проблему запоминания и использования опыта, т.е. применения элементов обучения.
При решении задач оперативного управления и планирования, по-видимому, нецелесообразно каждый раз, например, прокладывать маршрут следования груза по железной дороге с учётом огромного числа динамически возникающих факторов. Конечно, пользуются простыми эвристическими алгоритмами управления, достаточно детализированными и децентрализованными для возможности учёта постоянно изменяющихся условий и обстановки.
В то же время, пошаговая оптимизация примитивно вырождается в последовательно принимаемое решение вида: "я нахожусь в состоянии Х; куда двигаться (что делать) дальше?" Такая простая схема движения к оптимуму и порождает возможность априорного расчёта оптимальных стратегий изменения состояния системы для того, чтобы в рабочем режиме по функции цели и по текущему состоянию системы находить запомнившийся предпочтительный переход в соседнее состояние, уменьшающий значение этой функции.
Такая схема соответствует и идее ситуационного управления, и рассмотренной ранее схеме нейросетевой реализации управления.
К стратегии пошаговой оптимизации следует отнести и тактические игры, заключающиеся в последовательном выполнении противниками (преимущественно, двумя) действий, приводящих к минимизации некоторой целевой функции, например, функции потерь. Здесь перед отдельным игроком стоит проблема выбора наилучшего хода для сложившейся ситуации.
Для этого, несомненно, могут каждый раз рассчитываться все возможные варианты ходов с возможными ответными ходами. Может быть использован и теоретический опыт. Однако такой анализ требует огромной производительности вычислительных средств. Он недостаточно оперативен.
Здесь решение находится на основе анализа действий опытного игрока, помнящего эффективный выход из множества сложившихся ситуаций и эксплуатирующего свои способности ассоциативного мышления. Используется и коллективный опыт, теоретически обобщённый.
Автоматизация подобного анализа может быть произведена на основе разработки "подсказчика", хранящего в памяти большое количество ситуаций и рекомендующего следующий ход в соответствии с опытом экспертов, с историей и с теоретическим анализом.
Всё сказанное выше определяет целесообразность реализации с помощью логической нейронной сети.
Нейросетевая транспортная модель динамической маршрутизации
Транспортная сеть представляет собой конечное множество пунктов (узлов), соединённых между собой линиями связи. Ограничения на топологию связей отсутствуют.
Случайным образом или по некоторому закону (например, по расписанию) в сети возникают заявки на транспортное перемещение, на передачу сообщений или, в общем случае, — на движение объекта из пункта отправления к пункту назначения. Такими пунктами может быть любая пара пунктов сети. Заявки требуют прокладки маршрутов следования. Маршрут может предполагать как непосредственное перемещение из пункта отправления в пункт назначения (если существует связь), так и транзитное перемещение через промежуточные пункты.
При моделировании целесообразно наблюдать единичный акт перемещения по каждому маршруту: из одного пункта в другой. Это позволяет применять динамическое управление реализацией маршрутов и изменять условия продвижения от пункта отправления к пункту назначения.
Модель ориентирована на решение задачи "проникновения" из пункта отправления в пункт назначения кратчайшим или менее загруженным доступным путём, т.е. за минимально возможное время. Решение этой задачи характерно для маршрутизации в компьютерной сети, включая Интернет, для почтовой связи, оптимизации грузовых перевозок всех видов, нефтяных и газовых магистралей и др. В тоже время с помощью этой модели может быть составлено оптимальное транспортное расписание, например, движения поездов.
Для проекции сети на плоскость введём систему координат (х, у), позволяющую однозначно идентифицировать (адресовать) каждый из N пунктов сети. Координаты могут быть декартовыми, географическими и др. В соответствии с их назначением, знание их точного значения не обязательно.
Пусть 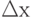 — разность координаты х пункта назначения и пункта нахождения (отправления или промежуточного пункта), из которого следует произвести шаг перемещения — смещение;
— разность координаты х пункта назначения и пункта нахождения (отправления или промежуточного пункта), из которого следует произвести шаг перемещения — смещение; 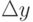 — аналогичная разность координаты у.
— аналогичная разность координаты у.
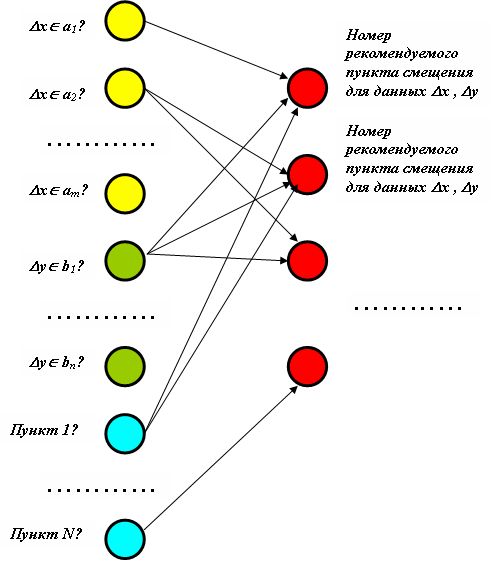
Для полной реализации модели достаточна однослойная логическая нейронная сеть (рис.9.1).
Разобьём весь интервал изменения 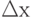 для данной транспортной сети на отрезки
для данной транспортной сети на отрезки  . За каждым отрезком закрепим нейрон рецепторного слоя. Возбуждение этого нейрона определяется достоверностью принадлежности найденного текущего значения
. За каждым отрезком закрепим нейрон рецепторного слоя. Возбуждение этого нейрона определяется достоверностью принадлежности найденного текущего значения 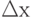 соответствующему отрезку.
соответствующему отрезку.
Весь интервал возможного изменения 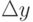 также разобьём на отрезки
также разобьём на отрезки  . За каждым отрезком закрепим нейрон-рецептор. Его возбуждение определяется достоверностью того, что текущее значение
. За каждым отрезком закрепим нейрон-рецептор. Его возбуждение определяется достоверностью того, что текущее значение 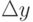 принадлежит соответствующему отрезку.
принадлежит соответствующему отрезку.
Закрепим N рецепторов за пунктами сети. Возбуждение этих рецепторов определяет пункт нахождения — пункт отправления или промежуточный пункт, из которого следует произвести смещение.
Выходной слой состоит из N нейронов. Их возбуждение определяет пункты, в которые необходимо или возможно произвести смещение.
Рекомендация по смещению не обязательно однозначна. Могут выдаваться варианты смещения, которые подлежат дополнительному анализу с учётом различных динамических факторов.
Синапсические связи вводятся так, чтобы каждое единичное возбуждение рецепторов всех элементов тройки {ai, bj, <k-й пункт нахождения>} приводил к максимальному возбуждению нейрона выходного слоя, называющего пункт дальнейшего смещения.
Функцию активации целесообразно выбрать, как  , где знаком
, где знаком  обозначают замену отрицательных значений нулём, т.е.
обозначают замену отрицательных значений нулём, т.е. 
Таким образом, первоначально по разностям координат х и у пункта отправления и пункта назначения отыскивается промежуточный пункт смещения. Для продолжения имитации движения возбуждается нейрон рецепторного слоя, закреплённый за полученным пунктом смещения, т.е. за новым пунктом нахождения. По его координатам и координатам пункта назначения вновь определяются 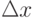 и
и 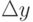 . Возбуждаются соответствующие этим разностям рецепторы, и для данного пункта нахождения вновь по максимальному возбуждению нейрона выходного слоя определяется следующий пункт смещения и т.д.
. Возбуждаются соответствующие этим разностям рецепторы, и для данного пункта нахождения вновь по максимальному возбуждению нейрона выходного слоя определяется следующий пункт смещения и т.д.
Координаты каждого полученного пункта смещения сравниваются с координатами пункта назначения, т.к. в случае их совпадения маршрут следования реализован.
Изменение весов связей и порогов позволяет ввести элементы динамического управления движением. Так, увеличение порога нейрона выходного слоя целесообразно связать с нагрузкой соответствующего пункта (узла). Величина возбуждения нейрона, указывающего на этот пункт, может при этом зависеть, например, от количества занятых путей станции (при "железнодорожной" интерпретации) или от количества занятых каналов обслуживания (базы данных).
Такое регулирование величины возбуждения нейронов выходного слоя позволяет строить транспортные сети с использованием резервных, обходных путей, т.к. исходные построения обученной нейросети можно производить с учётом не одного, а более пунктов смещения. Тогда пункт смещения, "возбудившийся" более других, может быть выбран для этого смещения.
Продвижение по сети с каждого пункта должно уменьшать значение соответствующего ему порога (на выходном слое) в зависимости от "физического смысла" задачи.
Регулировка синапсических весов нейрона выходного слоя может быть связана с загруженностью пути, линии передачи данных и других средств перемещения в транспортной сети. Такая регулировка требует введения дополнительного контроля состояния связи, соединяющей пункты. Синапсический вес такой связи должен снижаться при имитации движения. С этим снижением должен быть связан счётчик времени, в течение которого связь невозможна. Например, интервал следования поездов по одному пути обусловлен, в частности, необходимым расстоянием между поездами. В общем случае необходимо учитывать пропускную способность линий связи. По истечении определённого времени (когда счётчик "обнуляется") вес связи увеличивается до максимального (скорее всего, до единицы). Таким образом, даже если величина возбуждения нейрона, указывающего на пункт смещения, высока и позволяет принять движущийся объект, учитывается состояние средства связи.
Так как работа модели тактируется, то при запретах на смещение движущихся объектов нейросеть не подвергается изменению с увеличением модельного времени на такт. Уменьшаются лишь значения счётчиков задержки. При переходе к следующему такту модельного времени вновь исследуется возможность дальнейшего продвижения объектов с новыми значениями синапсических весов и порогов нейронов выходного слоя.
С помощью подобных счётчиков можно организовывать задержки в пунктах сети для имитации остановок движения, например, поездов.
При построении обученной нейронной сети, моделирующей транспортную сеть, целесообразно усилить влияние разностей координат пункта назначения и пункта отправления таким образом, чтобы учесть меньшее количество промежуточных пунктов следования. То есть, рекомендуемый пункт очередного смещения для "дальних" маршрутов может и дальше отстоять от пункта назначения или промежуточного пункта следования.
Модель транспортного маршрутизатора из центрального пункта отправления
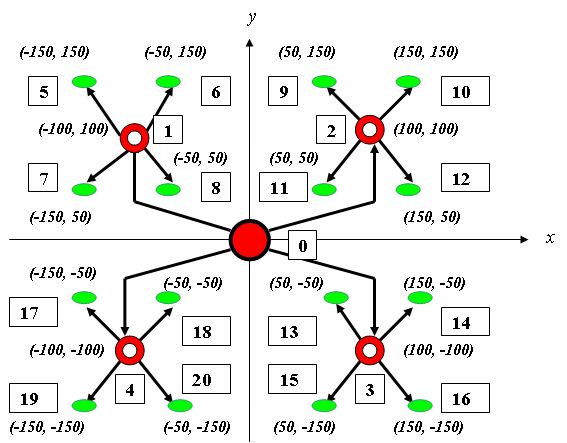
Рассмотрим пример транспортного маршрутизатора, планирующего движение из одного, центрального, пункта к периферийным пунктам со специальной топологией связей. Транспортная сеть представлена на рис.9.2, где все пункты заданы своими координатами (х, у) в системе координат, связанной с центром.
По величине и знаку разности координат пункта назначения и исходного или промежуточного пункта нахождения с помощью простейшей однослойной нейросети (рис.9.3) может быть найден пункт смещения, т.е. тот пункт, в который следует переместиться для дальнейшего следования. Целесообразно использовать рассмотренную ранее передаточную функцию, положив все веса равными единице, а пороги — равными двум.
Как рассматривалось выше, нейросеть отображает рекомендуемые смещения для всех возможных ситуаций, складывающихся на основе текущего нахождения объекта и соотношения между его координатами и координатами пункта назначения.
Если координаты найденного пункта смещения совпадают с координатами пункта назначения, маршрут реализован.
В противном случае отыскиваются разности координат пункта назначения и найденного пункта смещения. Они определяют единичное возбуждение соответствующих рецепторов входного слоя. Так же возбуждается рецептор, соответствующий найденному пункту смещения. Эти три возбуждённых рецептора вновь определяют новый пункт смещения.
Так продолжается до совпадения координат пункта смещения с координатами пункта назначения. В данном примере потребуется сделать не более двух шагов.
Например, при движении из пункта 0 по адресу пункта 6 с координатами (-50, 150) оказывается, что 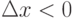 ,
, 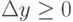 . Тогда нейрону 1 сообщается значение возбуждения, равное 1. Такое же значение сообщается нейрону 4, а также нейрону 5, соответствующему центральному пункту. Тогда
. Тогда нейрону 1 сообщается значение возбуждения, равное 1. Такое же значение сообщается нейрону 4, а также нейрону 5, соответствующему центральному пункту. Тогда . То есть, найден промежуточный пункт 1. Тогда возбуждение нейрона 6 полагается равным единице и устанавливается, что относительно пункта 1 координаты пункта назначения определяют неравенства
. То есть, найден промежуточный пункт 1. Тогда возбуждение нейрона 6 полагается равным единице и устанавливается, что относительно пункта 1 координаты пункта назначения определяют неравенства 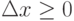 ,
, 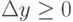 . Значит, следует сообщить единичное возбуждение нейронам 2 и 4. Возбуждение всех других рецепторов полагается нулевым. При расчёте функции активации для всех нейронов выходного слоя выдаётся рекомендация следования в пункт 6, т.к. единичное возбуждение приобретает нейрон 32. Маршрут составлен:
. Значит, следует сообщить единичное возбуждение нейронам 2 и 4. Возбуждение всех других рецепторов полагается нулевым. При расчёте функции активации для всех нейронов выходного слоя выдаётся рекомендация следования в пункт 6, т.к. единичное возбуждение приобретает нейрон 32. Маршрут составлен: 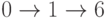 .
.
Нейросеть, представленная на рис.9.3, предполагает одностороннее перемещение — от центра к периферии. Поэтому конечные пункты оказались "зависшими", не влияющими на дальнейшее смещение. Однако легко развить эту нейросеть (нецелесообразно усложнять рисунок), предположив возможность возвращения в центральный пункт, или движения через центральный пункт, если задан маршрут из пункта отправления одного сектора в пункт назначения другого сектора. Внутри сектора движение может осуществляться через его локальный центральный пункт также на основе анализа указанной выше разности координат.
Таким образом, моделирование сложной транспортной сети любой природы с помощью логической нейронной сети оказывается исключительно простым и универсальным.