|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Алгоритмы Кронекера. Разложение на множители, свободные от квадратов. Факторизация
p-адический случай.
Формально алгоритм факторизации с использованием поля  - адической
метрики совпадает с алгоритмом, приведенным выше для поля
- адической
метрики совпадает с алгоритмом, приведенным выше для поля  :
:
А26. АЛГОРИТМ. (Факторизовать многочлен с помощью p-адической метрики)

Основные отличия заключаются в следующем.
Добавляется новый шаг алгоритма, заключающийся в выборе простого
числа  . На выбор его накладывается два условия: во-первых, при
переходе к
вычетам по модулю
. На выбор его накладывается два условия: во-первых, при
переходе к
вычетам по модулю  не должна понизиться степень полинома
не должна понизиться степень полинома  , т.е.
, т.е.  не
должно делить старший коэффициент полинома
не
должно делить старший коэффициент полинома  ; во-вторых, после
перехода к
классам по модулю
; во-вторых, после
перехода к
классам по модулю  полином
полином  должен остаться
свободным от квадратов, т.е.
должен остаться
свободным от квадратов, т.е.  не должно делить результант полиномов
не должно делить результант полиномов  и
и 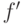 .
.
Отметим, что от выбора простого числа  может зависеть
количество
множителей в разложении полинома по модулю
может зависеть
количество
множителей в разложении полинома по модулю  . В некоторых
системах
выполняется разложение исходного полинома по модулю нескольких различных
значений
. В некоторых
системах
выполняется разложение исходного полинома по модулю нескольких различных
значений  (обычно до пяти значений), из них выбирается
такое
(обычно до пяти значений), из них выбирается
такое  ,
разложение по модулю которого имеет наименьшее количество сомножителей, и
разложение продолжается по этому модулю. Это замечание относится только ко
временным характеристикам алгоритма и носит вероятностный характер (нет
алгоритма, позволяющего проверить, что разложение по какому-то модулю имеет
минимальное возможное количество сомножителей).
,
разложение по модулю которого имеет наименьшее количество сомножителей, и
разложение продолжается по этому модулю. Это замечание относится только ко
временным характеристикам алгоритма и носит вероятностный характер (нет
алгоритма, позволяющего проверить, что разложение по какому-то модулю имеет
минимальное возможное количество сомножителей).
Далее, вместо рациональных чисел, приближающих вещественные
коэффициенты, будут использоваться классы по модулю  для
натуральных
значений
для
натуральных
значений  . Требуемая точность вычислений определяется как
натуральное число
. Требуемая точность вычислений определяется как
натуральное число  , так что для факторизации полинома
, так что для факторизации полинома ![f(x) \in \mathbb Z[x]](/sites/default/files/tex_cache/ef99ff92f5df8a33bd2d8ca08ea8be1a.png) нам нужно разложить на
множители этот полином по модулю
нам нужно разложить на
множители этот полином по модулю 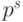 . Округление коэффициентов
полинома до
ближайшего целого состоит в том, что представители коэффициентов берутся из
симметричной системы вычетов.
. Округление коэффициентов
полинома до
ближайшего целого состоит в том, что представители коэффициентов берутся из
симметричной системы вычетов.
Как определить требуемую точность вычислений?
Предположим, что ![f(x), g(x) \in \mathbb Q[x]](/sites/default/files/tex_cache/1a9435a5711cf97cc20c0723b83c8a13.png) , причем
, причем  делит
делит  .
Предположим, что мы умеем оценивать сверху какой-то величиной
.
Предположим, что мы умеем оценивать сверху какой-то величиной  абсолютную
величину коэффициентов полинома
абсолютную
величину коэффициентов полинома  в зависимости от
коэффициентов
исходного полинома
в зависимости от
коэффициентов
исходного полинома  и от старшего коэффициента полинома
и от старшего коэффициента полинома  и от его
степени. Таким образом, ошибок округления при нахождении делителя исходного
полинома не будет, если используемая симметричная система содержит значения от
и от его
степени. Таким образом, ошибок округления при нахождении делителя исходного
полинома не будет, если используемая симметричная система содержит значения от  до
до  , т.е. , если
, т.е. , если  удовлетворяет
неравенству
удовлетворяет
неравенству  .
.
Учитывая предположение, что полином  не имеет линейных
делителей,
т.е. нужно искать неприводимые делители степени не выше
не имеет линейных
делителей,
т.е. нужно искать неприводимые делители степени не выше  , где
, где  , и максимальное значение старшего коэффициента
полинома
, и максимальное значение старшего коэффициента
полинома  равно старшему коэффициенту
равно старшему коэффициенту  исходного полинома, шаг
алгоритма
исходного полинома, шаг
алгоритма
Определить требуемую точность вычислений  }
}
принимает вид:
Найти наименьшее натуральное  , такое, что
, такое, что  .
.
Перейдем теперь к рассмотрению основного шага алгоритма:
Найти все неприводимые над 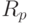 нормированные делители
нормированные делители  полинома
полинома  с точностью
с точностью  }
}
Детализируем его следующим образом.

Нулевое приближение разложения  в поле
в поле  - адических чисел
получается из разложения полинома
- адических чисел
получается из разложения полинома  в поле вычетов по модулю
в поле вычетов по модулю  . Это
разложение выполняется с помощью алгоритма Берлекэмпа.
. Это
разложение выполняется с помощью алгоритма Берлекэмпа.
Итерационный шаг уточнения разложения заключается в переходе от сравнения
по модулю 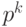 к сравнению по модулю
к сравнению по модулю  , где
, где  . Этот переход
выполняется с помощью леммы Гензеля. Наиболее часто используется случай
. Этот переход
выполняется с помощью леммы Гензеля. Наиболее часто используется случай  (квадратичный подъем) или
(квадратичный подъем) или  (линейный подъем). При этом в
одной и той же
системе могут применяться оба метода: сначала квадратичный, а после, когда
применение квадратичного метода приведет к слишком большим числам, -
линейный.
Итерационный процесс заканчивается, когда показатель степени
(линейный подъем). При этом в
одной и той же
системе могут применяться оба метода: сначала квадратичный, а после, когда
применение квадратичного метода приведет к слишком большим числам, -
линейный.
Итерационный процесс заканчивается, когда показатель степени  будет не
меньше значения
будет не
меньше значения  , определенного выше. В качестве
представителей системы
вычетов по модулю
, определенного выше. В качестве
представителей системы
вычетов по модулю  берется сбалансированная система, т.е. целые
числа, не
превосходящие по абсолютной величине числа
берется сбалансированная система, т.е. целые
числа, не
превосходящие по абсолютной величине числа  .
.
Проверка испытуемой комбинации на получение делителя полинома  осуществляется пробным делением.
осуществляется пробным делением.
Отметим, что при переборе возможных комбинаций сомножителей мы можем
ограничиться случаем, когда рассматриваемая комбинация содержит не более
половины из общего количества неприводимых (над 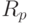 )
сомножителей.
)
сомножителей.
С учетом сделанных замечаний алгоритм факторизации принимает вид:
А27. АЛГОРИТМ (разложить на неприводимые  ).
).
![\begin{equation}
\text{Дано: \quad $f(x) \in\mathbb Z[x]$ }\\
\text{ Надо: \qquad $G$-разложение;} \\
\text{Переменные:\quad $U$- разложение}\\
\text{\qquad множество $M$ элементов типа $\N$}\\
\text{Начало}\\
\text{выбрать простое число $p$}\\
\text{\qquad \qquad \qquad \quad // $p$ не должно делить $\textrm{lc} (f)$ и
результант $(f,f')$}\\
\text{$B := 2^{m-1} \| f\|$\qquad \qquad \qquad \quad // оценивается необходимая
точность вычислений}\\
\text{$s := [\log_p B] + 1$}\\
\text{$q := p^s$}\\
\text{$f_1 (x) := \dfrac{f(x)}{\textrm{lc} (f)}\pmod q$}\\
\text{$U:=$нулевое приближение разложения $f_1 (x)$}\\
\text{поднять разложение $U$ до разложения по модулю $q$} \\
\text{\qquad \qquad \qquad // достигается кратным применением леммы Гензеля}\\
\text{$r := U.$число\_множителей}\\
\text{$t := 1$}\\
\text{$M := \{ 1, \dots, r\}$}\\
\text{цикл пока $t\leq [r/2]$}\\
\text{\qquad цикл для каждого подмножества $\{ i_1 , \dots, i_t \} \subset M$ пока $t\leq [\frac r2]$}\\
\text{\qquad \qquad $g(x) := \textrm{lc} (f) u_{i_1}(x) u_{i_2}(x) \dots u_{i_t}(x)$}\\
\text{\qquad \qquad $g(x) := g(x)/\cont(g)$}\\
\text{\qquad \qquad если $f(x)$ делится на $g(x)$ то}\\
\text{\qquad \qquad \qquad $G$.добавить $g(x)$}\\
\text{\qquad \qquad \qquad $f(x) := f(x)/g(x)$}\\
\text{\qquad \qquad \qquad $r := r - t$}\\
\text{\qquad \qquad \qquad $M$.удалить $\{i_1, i_2 ,\dots, i_t\}$}\\
\text{\qquad \qquad конец если}\\
\text{\qquad конец цикла}\\
\text{\qquad $t := t + 1$}\\
\text{конец цикла}\\
\text{$G$.добавить $f(x)$}\\
\text{Конец}
\end{equation}](/sites/default/files/tex_cache/a4b7a2cb8f9f9bf6d4a3e5f2895321e4.png)
