|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Алгоритмы Кронекера. Разложение на множители, свободные от квадратов. Факторизация
Разложение на множители, свободные от квадратов
Разложение многочлена на множители начнем с
приведения его к некоторому каноническому виду.
Прежде всего найдем НОД его коэффициентов, эта
величина называется содержанием многочлена  и
обозначается
и
обозначается  . Далее разложим многочлен
. Далее разложим многочлен  на свободные от квадратов множители , т. е. на
такие множители, которые являются произведениями
взаимно простых неприводимых многочленов в первой степени. Это можно сделать
путем дифференцирования исходного многочлена и
нахождения общих
делителей многочлена и его производной. Свободный от квадратов многочлен,
содержание которого
равно 1, назовем примитивным.
на свободные от квадратов множители , т. е. на
такие множители, которые являются произведениями
взаимно простых неприводимых многочленов в первой степени. Это можно сделать
путем дифференцирования исходного многочлена и
нахождения общих
делителей многочлена и его производной. Свободный от квадратов многочлен,
содержание которого
равно 1, назовем примитивным.
В принятых нами обозначениях алгоритм факторизации многочлена  принимает следующий вид.
принимает следующий вид.
А18. АЛГОРИТМ (факторизовать_многочлен).
![\begin{equation}\\
\text{\textbf{Дано:}\quad $f\in\mathbb Z[x]$ }\\
\text{\textbf{Надо:} \qquad $\textrm{cont}(f)$- содержание многочлена $f$} \\
\text{\qquad \qquad \qquad $U$- разложение}\\
\text{\textbf{Переменные:}\quad
$G$- разложение на свободные от квадратов} \\
\text{\qquad \qquad \qquad \qquad $V$- разложение текущего многочлена из $G$}
\\
\text{\textbf{Обозначения}:\quad $s == G.\text{число\_множителей}$}\\
\text{\qquad \qquad \qquad \qquad $g == G.\text{множители}$}\\
\text{\qquad \qquad \qquad \qquad $u == U.\text{множители}$} \\
\text{ \qquad \qquad \qquad \qquad $v == V.\text{множители}$}\\
\textbf{Начало} \\
\text{$u.$начать работу }\\
\text{вычислить} \textrm{cont}$(f)$ }\\
\text{$f(x) := f(x)/$}\textrm{cont}$(f)$ \\
разложить\_на\_свободные\_от\_квадратов $(f,G)}$\\
\text{\qquad \qquad \qquad \qquad $f(x) = g_1 (x)g_2^2(x)\dots g_s^s(x),$}\\
\textbf{цикл для} $i$ \textbf{от} 1 \textbf{до} $s$ \\
\text{\qquad \qquad факторизовать примитивный, свободный от квадратов $(g_i,
v)$}\\
\text{\qquad \qquad $u$.добавить $v^i$}\\
\textbf{конец цикла}\\
\textbf{Конец}
\end{equation}](/sites/default/files/tex_cache/f4de0760af9225eb2edfec690ade1f0f.png)
Вычисление содержания многочлена сводится к вычислению наибольшего общего делителя целых чисел. Поскольку мы предполагаем коэффициенты не слишком большими, вполне достаточно ограничиться алгоритмом Евклида нахождения НОД.
Разложение примитивного (без нетривиальных общих делителей коэффициентов) многочлена на свободные от квадратов множители осуществляется следующим образом.
А19. АЛГОРИТМ (разложить_на_свободные_от_квадратов).
![\begin{equation}\\
\text{Дано:\quad $f(x)\in\mathbb Z[x]$; $\textrm{cont}(f)=1$ }\\
\text{Надо:\qquad $G$-разложение }\\
\text{Переменные:\quad $h$, $c$, $d\in\mathbb Z[x]$} \\
\text{\qquad \quad \quad \quad \quad \quad $k\in\mathbb N$} \\
\text{Обозначения:\quad $s == G.$число\_множителей} \\
\text{\qquad \quad \quad \quad \quad \quad $g == G.$множители} \\
\text{Начало} \\
\text{$h(x) := \GCD(f(x), f'(x))$, где $f'(x)=df(x)/dx$} \\
\text{$c(x) := f(x)/h(x)$} \\
\text{$d(x) := (df(x)/dx)/h(x) - dc(x)/dx$} \\
\text{$k := 1$} \\
\text{цикл пока $c(x)\ne 1$}\\
\text{\qquad $g_k(x) := \GCD (c(x), d(x))$}\\
\text{\qquad $c(x) := c(x)/g_k(x)$}\\
\text{\qquad $d(x) := d(x)/g_k(x) - dc(x)/dx$}\\
\text{\qquad $k := k+1$}\\
\text{конец цикла} \\
\text{$s := k-1$ }\\
\text{Конец}
\end{equation}](/sites/default/files/tex_cache/e6814782e196ec99b13a3ec31d91a6d9.png)
Для доказательства корректности этого алгоритма предположим, что  , где
, где  свободны от
квадратов и
взаимно просты. Тогда
свободны от
квадратов и
взаимно просты. Тогда ![h =\smash[t]{\prod\limits_{i=2}^s} g_i^{i-1}](/sites/default/files/tex_cache/10fe4a9b37f86ae859515b78d3feb3f3.png) , до начала цикла
, до начала цикла

В теле цикла выполняется присваивание многочленам 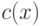 и
и 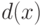 значений
значений

15.1. УПРАЖНЕНИЕ.
Построить аналог алгоритма A19 для
многочленов с коэффициентами из поля 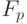 .
.
Алгоритмы разложения на неприводимые множители примитивного свободного от квадратов многочлена с целыми коэффициентами составляют главное содержание данной лекции.
Современные алгоритмы разложения примитивного свободного от квадратов
многочлена  на неприводимые множители основаны на следующих
соображениях. Кольцо целых чисел
на неприводимые множители основаны на следующих
соображениях. Кольцо целых чисел  вкладывается в полное
нормированное поле
вкладывается в полное
нормированное поле 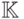 . Предполагается, что мы умеем
раскладывать на множители
многочлены из кольца
. Предполагается, что мы умеем
раскладывать на множители
многочлены из кольца ![\mathbb K[x]](/sites/default/files/tex_cache/8a6f8af632ec00b1b99f9ebc8d18fb38.png) , т. е. для любого наперед заданного
числа
, т. е. для любого наперед заданного
числа  можем вычислить с абсолютной точностью
можем вычислить с абсолютной точностью 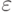 коэффициенты всех неприводимых делителей данного многочлена
(предполагается
некоторая нормировка делителей, например, равенство единице старшего
коэффициента). Каждому
неприводимому в
коэффициенты всех неприводимых делителей данного многочлена
(предполагается
некоторая нормировка делителей, например, равенство единице старшего
коэффициента). Каждому
неприводимому в ![\mathbb K[x]](/sites/default/files/tex_cache/8a6f8af632ec00b1b99f9ebc8d18fb38.png) делителю
делителю 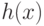 многочлена
многочлена  соответствует однозначно определенный неприводимый в
соответствует однозначно определенный неприводимый в ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) делитель
делитель  многочлена
многочлена  ,
который делится на
,
который делится на 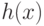 (более точно,
(более точно,  представляет собой произведение нескольких неприводимых в
представляет собой произведение нескольких неприводимых в ![\mathbb K[x]](/sites/default/files/tex_cache/8a6f8af632ec00b1b99f9ebc8d18fb38.png) делителей
многочлена
делителей
многочлена  , если,
конечно, сам
, если,
конечно, сам 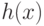 не принадлежит
не принадлежит ![\mathbb Q[x]](/sites/default/files/tex_cache/f3d1f8b27dd29107881f26927fbcc385.png) ). Для
нахождения неприводимого в
). Для
нахождения неприводимого в ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) делителя многочлена
делителя многочлена  либо используют
перебор произведений
различных подмножеств неприводимых в
либо используют
перебор произведений
различных подмножеств неприводимых в ![\mathbb K[x]](/sites/default/files/tex_cache/8a6f8af632ec00b1b99f9ebc8d18fb38.png) делителей
многочлена
делителей
многочлена  , либо для восстановления
, либо для восстановления  по
по 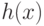 пользуются следующим методом.
Ограничивают возможную степень многочлена
пользуются следующим методом.
Ограничивают возможную степень многочлена  положительным
числом
положительным
числом  ;
выделяют свободный
;
выделяют свободный  -модуль
ранга
-модуль
ранга 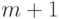 в модуле многочленов с целыми коэффициентами степени
не выше
в модуле многочленов с целыми коэффициентами степени
не выше  , в котором должен находиться искомый многочлен
, в котором должен находиться искомый многочлен  , в частности,
выделенный модуль может совпадать со всем множеством многочленов степени не
выше
, в частности,
выделенный модуль может совпадать со всем множеством многочленов степени не
выше  , вкладывают этот модуль в евклидово
пространство над полем
, вкладывают этот модуль в евклидово
пространство над полем  так, чтобы многочлену
так, чтобы многочлену  соответствовал
кратчайший вектор в выделенном модуле, называемом обычно решеткой, и
находят этот кратчайший
вектор.
соответствовал
кратчайший вектор в выделенном модуле, называемом обычно решеткой, и
находят этот кратчайший
вектор.
