|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Алгоритмы Кронекера. Разложение на множители, свободные от квадратов. Факторизация
Выделение линейных множителей.
Прежде чем переходить к общим алгоритмам разложения многочленов на неприводимые множители, рассмотрим случай, когда у многочлена имеются линейные множители. Нахождение линейных множителей осуществляется значительно проще, чем в общем случае нахождение неприводимых множителей. В большинстве систем компьютерной алгебры, прежде чем применять общие методы факторизации, у многочлена выделяются линейные множители.
Нахождение линейных множителей основано на теореме Безу, которая
утверждает, что если рациональное число 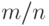 , где
, где  -целое,
-целое,  -
натуральное,
-
натуральное,  , является корнем многочлена с целыми
коэффициентами, то
, является корнем многочлена с целыми
коэффициентами, то  делит старший коэффициент этого многочлена,
а
делит старший коэффициент этого многочлена,
а  делит его свободный член. Кроме того, между рациональными
корнями многочлена и его линейными множителями существует взаимно
однозначное соответствие:
делит его свободный член. Кроме того, между рациональными
корнями многочлена и его линейными множителями существует взаимно
однозначное соответствие: 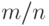 является корнем многочлена
является корнем многочлена ![f(x)\in \mathbb Z[x]](/sites/default/files/tex_cache/8049b0ca71684c4e56d841d8cdedce16.png) тогда и только тогда, когда
тогда и только тогда, когда  делится на
делится на  (предполагается, что
(предполагается, что  и
и  взаимно простые
числа).
взаимно простые
числа).
А20. АЛГОРИТМ (рациональные_корни).
![\begin{equation}\\
\text{Дано:\quad $f(x)\in\mathbb Z[x]$} \\
\text{ Надо:\qquad $M$- стек элементов типа $\mathbb Q$ (рациональные корни $f(x)$)}\\
\text{\qquad $g(x)$- делитель максимальной степени многочлена
$(x)$,}\\
\text{\qquad \qquad не имеющий рациональных корней.}\\
\text{ Начало}\\
\text{$M.$ начать работу} \\
\text{$a := f.$ старший коэффициент} \\
\text{$b := f.$ свободный член} \\
\text{$g(x) := f(x)$ }\\
\text{цикл для всех $(p,q)$, где $p\in\mathbb N$, q\in\mathbb Z$,
$p|a$, $q|b$, НОД$(p,q)=1$}\\
\text{\qquad $r:= $ остаток от деления $g(x)$ на $px-q$}\\
\text{\qquad \qquad // т. е. $g(x) = (px-q)\cdot h(x) + r$}\\
\text{\qquad если $r=0$, то}\\
\text{\qquad \qquad $M.$ добавить $q/p$}\\
\text{\qquad \qquad $g(x) := h(x)$}\\
\text{\qquad конец если}\\
\text{ конец цикла} \\
\text{ Конец}
\end{equation}](/sites/default/files/tex_cache/7ca3d44fa57c0a8851665946b3e1677d.png)
Организация перебора.
15.2. Организация перебора. Простейший случай:
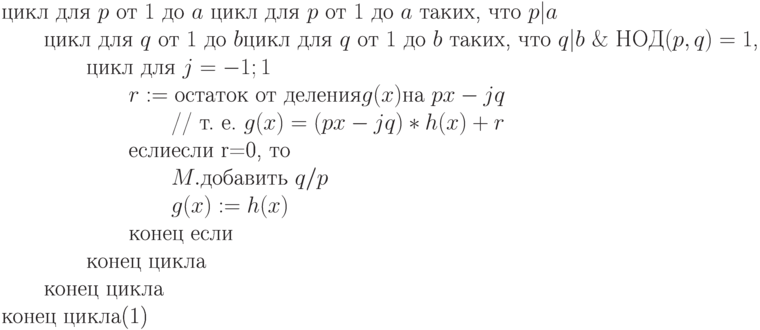
15.3. Перебор с предварительным разложением старшего коэффициента и свободного члена на простые множители.
Мы предполагаем, что количество простых чисел, на которые делятся  или
или  , невелико (не превосходит
, невелико (не превосходит 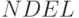 ). Эти числа располагаются
в массиве
). Эти числа располагаются
в массиве  , соответствующие показатели степеней- в
, соответствующие показатели степеней- в  и
и  . Числа
. Числа  и
и  задаются векторами
задаются векторами 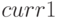 и
и  , которые
содержат показатели степеней простых делителей чисел
, которые
содержат показатели степеней простых делителей чисел  и
и  соответственно.
соответственно.

А 21. АЛГОРИТМ NEXTP.

А 22. АЛГОРИТМ NEXTQ.

