|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Алгоритмы Кронекера. Разложение на множители, свободные от квадратов. Факторизация
Факторизация, основанная на переборе неприводимых сомножителей в K[x]
Общая схема.
Рассмотрим вложение кольца целых чисел  в поле комплексных
чисел
в поле комплексных
чисел 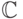 .
Основная теорема алгебры утверждает, что в кольце
.
Основная теорема алгебры утверждает, что в кольце ![\mathbb C[x]](/sites/default/files/tex_cache/ad69761f9cc540c0b26512c26db28809.png) всякий полином
разлагается на линейные множители. Можно считать, что это разложение имеет вид
всякий полином
разлагается на линейные множители. Можно считать, что это разложение имеет вид

 - старший
коэффициент полинома
- старший
коэффициент полинома  , а
, а  - его корни. Если
- его корни. Если 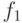 - делитель полинома
- делитель полинома  в кольце
в кольце ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) ,
то в
,
то в ![\mathbb C[x]](/sites/default/files/tex_cache/ad69761f9cc540c0b26512c26db28809.png) имеет место разложение
имеет место разложение
 - целое число,
делящее
- целое число,
делящее  , а
, а  -
подмножество множества индексов
-
подмножество множества индексов  . С другой стороны, если полином
. С другой стороны, если полином 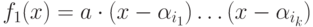 принадлежит
принадлежит ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) , то
полином
, то
полином  также принадлежит
также принадлежит ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) и делит
и делит  . Таким образом можно
предложить следующий метод факторизации полинома
. Таким образом можно
предложить следующий метод факторизации полинома ![f(x) \in
\mathbb Z[x]](/sites/default/files/tex_cache/747b7aadea0134982e3461e538e2f81d.png) .
.А23. АЛГОРИТМ (Факторизовать перебором комплексных корней).
![\begin{equation}\\
\text{Начало}\\
\text{Найти все комплексные корни $\alpha_1,\dots,\alpha_n$ полинома
$f$}\\
\text{$I:=\{1,\dots,n\}$}\\
\text{цикл для каждого подмножества $\{ i_1,\dots,i_k\} \subset I$}\\
\text{если $g(x) = a\cdot (x-\alpha_{i_1})\dots(x-\alpha_{i_k})$ принадлежит $\mathbb Z[x]$
то}\\
\text{\qquad \qquad запомнить множитель $g(x) := g(x)/\cont(g(x))$}\\
\text{\qquad \qquad $f(x) := f(x)/g(x)$}\\
\text{\qquad \qquad $I:=I\setminus\{i_1,\dots,i_k\}$}\\
\text{\qquad конец если}\\
\text{конец цикла}\\
\text{Конец}
\end{equation}](/sites/default/files/tex_cache/a4d2e52be82ef1a9b25d8dcf17a0d1a4.png)
Если цикл по подмножествам индексов организован так, что вначале рассматриваются множества, состоящие из одного элемента, затем - из двух и т. д., то выделяемый на очередном шаге множитель будет неприводимым и задача факторизации будет полностью решена.
К сожалению, описанный подход не является решением задачи факторизации
даже с "классической" точки зрения, поскольку в общем случае мы не можем
"за
конечное число шагов" найти даже один корень полинома. Однако мы можем
находить корни полинома с любой наперед заданной точностью. При этом возникает
другая проблема. Если корни полинома вычислены приближенно, то мы не можем
проверить, принадлежит ли полином  кольцу
кольцу ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) .
.
Однако, если точность выбрана достаточно высокой, то эту проверку мы
можем заменить двумя шагами: округлить коэффициенты полинома  до ближайшего
целого, и проверить, делит ли получившийся полином исходный полином
до ближайшего
целого, и проверить, делит ли получившийся полином исходный полином  .
Получаем:
.
Получаем:
А24. АЛГОРИТМ (с учетом точности вычислений).

Для практической реализации данного метода нужно детализировать алгоритмы выбора точности вычислений и нахождения корней полинома.
Выбор точности определяется следующим условием: если
![g(x) = a\cdot (x-\alpha_{i_1})\dots(x-\alpha
_{i_k})\in\mathbb Z[x]](/sites/default/files/tex_cache/b52399ec1ba34a6f78cfddd7bfe1df93.png)
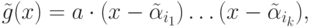
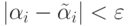 , то
коэффициенты полинома
, то
коэффициенты полинома  по
модулю меньше 1/2. На основе оценок значений корней эта задача не представляет
особой сложности.
по
модулю меньше 1/2. На основе оценок значений корней эта задача не представляет
особой сложности.16.1. УПРАЖНЕНИЕ.
Используя границы для корней многочлена, оценить значение 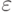 .
.
Для нахождения всех комплексных корней полинома можно воспользоваться комплексным аналогом метода Штурма, позволяющим определить количество корней полинома в заданном прямоугольнике комплексной плоскости [ 28 ] , а далее - методом дихотомии. Однако гораздо чаще для нахождения комплексных корней полинома используются разновидности метода Ньютона. Эти методы разрабатываются в численном анализе, и мы не будем здесь останавливаться на них.
Для сокращения перебора можно воспользоваться тем, что корни исходного
полинома (коэффициенты которого предполагаются целыми числами), не являющиеся
действительными, распадаются на пары комплексно-сопряженных, при
этом
комплексно-сопряженные корни относятся к одному и тому же неприводимому над  делителю исходного полинома. Это замечание позволяет
переписать алгоритм
без использования комплексных чисел.
делителю исходного полинома. Это замечание позволяет
переписать алгоритм
без использования комплексных чисел.
А25. АЛГОРИТМ (факторизовать с помощью разложения над R ).

Проанализируем предлагаемый алгоритм. Он основан на том, что любое действительное число является пределом фундаментальной последовательности рациональных чисел и любая фундаментальная последовательность рациональных чисел сходится к действительному числу. Арифметические операции являются при этом непрерывными. При реальных вычислениях на компьютере мы используем итерационные методы, т.е. строим фундаментальные последовательности, сходящиеся к коэффициентам делителей исходного полинома.
Определение фундаментальной и сходящейся последовательности чисел основано на понятии расстояния между двумя числами. В поле действительных чисел расстояние между двумя числами определяется как абсолютная величина разности этих чисел. Метрики такого типа относятся к так называемым архимедовым метрикам. Поле действительных чисел часто определяют как пополнение поля рациональных чисел по архимедовой метрике, т.е. множество классов эквивалентности фундаментальных последовательностей рациональных чисел; при этом две последовательности считаются эквивалентными, если разность между ними - бесконечно малая величина.
Кроме архимедовой, на поле рациональных чисел имеются более экзотические
метрики, так называемые неархимедовы или  - адические.
Они используются при
решении многих алгебраических и теоретико-числовых задач. В частности,
- адические.
Они используются при
решении многих алгебраических и теоретико-числовых задач. В частности,  - адическая метрика оказывается более полезной, чем
архимедова при
факторизации полиномов.
- адическая метрика оказывается более полезной, чем
архимедова при
факторизации полиномов.
Применение ее для решения задач факторизации стало возможным после того,
как был получен достаточно эффективный метод разложения полиномов на множители
над полем  - адических чисел. Этот метод состоит из двух
ключевых алгоритмов:
первый из них, алгоритм Берлекэмпа, позволяет достаточно быстро разлагать на
множители полиномы с коэффициентами из конечного поля, что соответствует
нахождению нулевого приближения разложения в описанном выше алгоритме; второй
представляет
- адических чисел. Этот метод состоит из двух
ключевых алгоритмов:
первый из них, алгоритм Берлекэмпа, позволяет достаточно быстро разлагать на
множители полиномы с коэффициентами из конечного поля, что соответствует
нахождению нулевого приближения разложения в описанном выше алгоритме; второй
представляет  - адический аналог метода Ньютона.
Математический результат, на
котором он основан, носит название леммы Гензеля. Метод факторизации,
базирующийся на алгоритме Берлекэмпа и лемме Гензеля, принят во многих
системах
компьютерной алгебры.
- адический аналог метода Ньютона.
Математический результат, на
котором он основан, носит название леммы Гензеля. Метод факторизации,
базирующийся на алгоритме Берлекэмпа и лемме Гензеля, принят во многих
системах
компьютерной алгебры.
