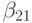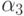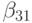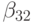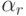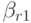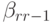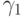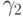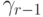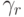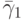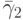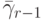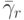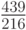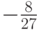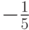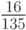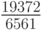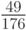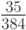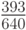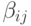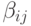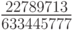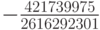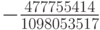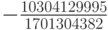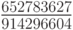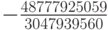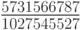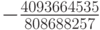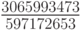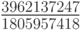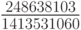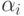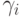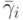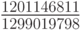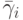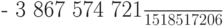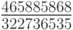НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 9: Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский физико-технический институт

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать программу

Значения коэффициентов классического метода Рунге - Кутты (четвертого порядка аппроксимации ) указаны в табл. 8.6. Правило трех восьмых (четвертый порядок аппроксимации ) представлено в табл. 8.7. Этот метод имеет, по - видимому, наименьшую погрешность среди явных схем Рунге - Кутты четвертого порядка аппроксимации. Метод Бутчера (шестой порядок аппроксимации ) указан в табл. 8.8. Очевидна связь между методами, приведенными в таблицах 8.5 и 8.6 с формулой Симпсона численного интегрирования.

Таблица 8.6.
0
1/2	1/2
1/2	0	1/2
1	0	0	1
	1/6	2/6	2/6	1/6

Таблица 8.7.
0
1/3	1/3
2/3	- 1/3	1
1	1	- 1	1
	1/8	3/8	3/8	1/8

По - видимому, наивысший порядок аппроксимаций (десятый) был получен в работах Куртиса [8.4], позже — Хайрера [8.5]. Соответствующие коэффициенты не приведены ввиду их громоздкости.

Таблица 8.8.
0
1/2	1/2
2/3	2/9	4/9
1/3	7/36	2/9	- 1/12
5/6	- 35/144	- 55/36	35/48	15/8
1/6	- 1/360	- 11/36	- 1/8	1/2	1/10
1	- 41/260	22/13	43/156	- 118/39	32/195	80/39
	13/200	0	11/40	11/40	4/25	4/25	13/200

В численной практике используются также так называемые вложенные формулы Рунге - Кутты [8.3], [8.6], [8.7], в которых наряду с соотношением

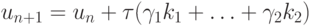${u_{n + 1} = u_n + {\tau}(\gamma_1k_1 + \ldots + \gamma_2k_2)}$

( 8.5)

используется соотношение того же вида, но с другим набором весовых множителей

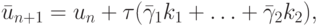${\bar u_{n + 1} = u_n + {\tau}(\bar {\gamma}_1 k_1 + \ldots + \bar {\gamma}_2 k_2 ), }$

( 8.6)

причем порядки аппроксимации в них различаются: q — порядок аппроксимации (8.6), а p — (8.5). В этом случае порядок метода указывается, как p(q), а таблица Бутчера имеет вид табл. 8.9. Последнюю строчку в этой таблице иногда называют оценщиком погрешности.

Таблица 8.9.
0
$\alpha_2$	$\beta_{21}$
$\alpha_3$	$\beta_{31}$	$\beta_{32}$
$\ldots$	$\ldots$	$\ldots$	$\ldots$
$\alpha_r$	$\beta_{r1}$	$\beta_{r2}$	$\ldots$	$\beta_{rr - 1}$
u₁	$\gamma_1$	$\gamma_2$	$\ldots$	$\gamma_{r - 1}$	$\gamma_r$
u₂	$\bar {\gamma}_1$	$\bar {\gamma}_2$	$\ldots$	$\bar {\gamma}_{r - 1}$	$\bar {\gamma}_r$

Приближения точного решения с разными остаточными членами (8.5) и (8.6) позволяют оценить погрешность численного метода, полученную в конкретном расчете, и служат для повышения точности еще на один порядок в каждой точке или (что бывает чаще) для автоматического выбора длины следующего шага интегрирования (см. 8.4).

Приведем несколько наиболее известных вложенных методов Рунге - Кутты. Метод Фельберга 2(3) представлен в табл. 8.10, метод Ческино 2(4) — в табл. 8.11.

Таблица 8.10.
0
1	1
1/2	1/4	1/4
	1/2	1/2	0
	1/6	1/6	4/6

Таблица 8.11.
0
1/4	1/4
1/2	0	1/2
1	1	- 2	2
	1	- 2	2	0
	1/6	0	4/6	1/6

Метод Кутты - Мерсона 4(5) приведен в табл. 8.12. Этот метод — наиболее простой среди вложенных методов Рунге - Кутты порядка 4(5), поскольку требует небольшого числа обращений к функциям вычисления правых частей системы уравнений (8.1) и имеет простые коэффициенты.

Таблица 8.12.
0
1/3	1/3
1/3	1/6	1/6
1/2	1/8	0	3/8
1	1/2	0	- 3/2	2
	1/2	0	- 3/2	2	0
	1/6	0	0	2/3	1/6

Для 5 этапного метода Кутты - Мерсона 4(5) приведем подробные расчетные формулы:

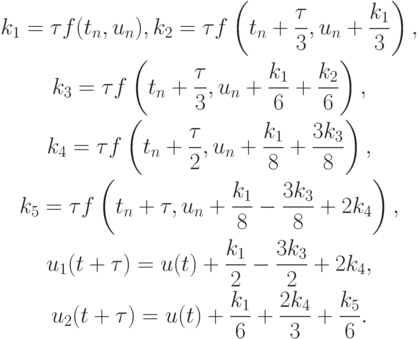
$\begin{gather*} k_1 = {\tau}f(t_n, u_n), k_2 = {\tau}f\left({t_n + \frac{{\tau}}{3}, u_n + \frac{{k_1 }}{3}}\right), \\ k_3 = {\tau}f\left({t_n + \frac{{\tau}}{3}, u_n + \frac{{k_1 }}{6} + \frac{{k_2 }}{6}}\right), \\ k_4 = {\tau}f\left({t_n + \frac{{\tau}}{2}, u_n + \frac{{k_1 }}{8} + \frac{{3k_3 }}{8}}\right), \\ k_5 = {\tau}f\left({t_n + {\tau}, u_n + \frac{{k_1 }}{8} - \frac{{3k_3 }}{8} + 2k_4 }\right), \\ u_1 (t + {\tau}) = u(t) + \frac{{k_1 }}{2} - \frac{{3k_3 }}{2} + 2k_4, \\ u_2 (t + {\tau}) = u(t) + \frac{{k_1 }}{6} + \frac{{2k_4 }}{3} + \frac{{k_5}}{6}. \end{gather*}$

Рассмотрим вкратце другие вложенные методы и соответствующие им таблицы. Метод Фельберга 4(5) представлен в табл. 8.13, метод Дормана - Принса 5(4) — в табл. 8.14 (см. также [8.6]).

Таблица 8.13.
0
1/4	1/4
3/8	3/32	9/32
$\frac{12}{13}$	$\frac{1 932}{2 197}$	$\frac{7 296}{2 197}$
1	$\frac{439}{216}$	- 8	$\frac{3 680}{513}$	$- \frac{845}{4 104}$
$\frac{1}{2}$	$- \frac{8}{27}$	2	$- \frac{3 544}{2 565}$	$\frac{1 859}{4 104}$	$- \frac{14}{40}$
	$\frac{25}{216}$	0	$\frac{1 408}{2 565}$	$\frac{2 197}{4 104}$	$- \frac{1}{5}$	0
	$\frac{16}{135}$	0	$\frac{6 656}{12 825}$	$\frac{28 561}{56 430}$	$- \frac{9}{50}$	$\frac{2}{55}$

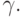
Этот метод замечателен тем, что он не только минимизирует остаточный член в оценщике погрешностей, но и требует меньшей памяти для хранения таблицы коэффициентов метода. Действительно, последняя строка $\beta$ совпадает с одной из строк $\gamma.$

С методом Фельберга более высокого порядка 7(8) можно ознакомиться в [8.8], значения его коэффициентов приведены в табл. 8.15.

Среди современных методов решения нежестких систем ОДУ наилучшие результаты дает метод Дормана - Принса 8(7). Он обладает наименьшей погрешностью среди всех схем порядка 8, коэффициенты указаны в табл. 8.16, 8.17. С вложенными формулами Рунге - Кутты, разработанными в 90 - х годах, можно ознакомиться в монографии [8.10].

Таблица 8.14.
0
1/5	1/5
3/10	3/40	9/40
4/5	44/45	- 56/15	32/9
$\frac{8}{9}$	$\frac{19 372}{6 561}$	$- \frac{25 360}{2 187}$	$\frac{64 448}{6 561}$	$- \frac{212}{729}$
1	$\frac{9 017}{3 168}$	$- \frac{355}{33}$	$\frac{46 732}{5 247}$	$\frac{49}{176}$	$- \frac{5 163}{18 656}$
1	$\frac{35}{384}$	0	$\frac{500}{1 113}$	$\frac{125}{192}$	$- \frac{2 187}{6 784}$	$\frac{11}{84}$
	$\frac{35}{384}$	0	$\frac{500}{1 113}$	$\frac{125}{192}$	$- \frac{2 187}{6 784}$	$\frac{11}{84}$	0
	$\frac{5 179}{57 600}$	0	$\frac{7 571}{16 695}$	$\frac{393}{640}$	$- \frac{92 097}{339 200}$	$\frac{187}{2 100}$	$\frac{1}{40}$

методы Рунге - Кутты — это одношаговые методы, так как позволяют найти значение искомой функции в точке t_{n + 1} используя только значение функции в точке t_n. При этом не учитывается информация о функции, накопленная на предыдущих этапах расчета. Такая информация может быть полезна при решении жестких задач или при автоматическом выборе следующего шага интегрирования.

Один из способов учета предыстории заключается в использовании общих многошаговых методов. Частный случай — методы Адамса — рассмотрен в следующем параграфе. Другой способ учета описан в 8.4.

Таблица 8.15.
0
2/27	2/27
1/9	1/36	1/12
1/6	1/24	0	1/8
5/12	5/12	0	- 25/16	25/16
1/2	1/20	0	0	1/4	1/5
5/6	- 25/108	0	0	125/108	- 65/27	125/54
1/6	31/300	0	0	0	61/225	- 2/9	13/900
2/3	2	0	0	- 53/6	704/45	- 107/9	67/90	3
1/3	- 91/108	0	0	23/108	- 976/135	311/54	- 19/60	17/6	- 1/12
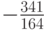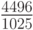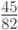1	$\frac{2383}{4100}$	0	0	$- \frac{341}{164}$	$\frac{4496}{1025}$	$- \frac{301}{82}$	$\frac{2133}{4100}$	$\frac{45}{82}$	$\frac{45}{164}$	$\frac{18}{41}$
0	3/205	0	0	0	0	- 6/41	- 3/205	- 3/41	3/41	6/41	0
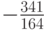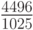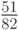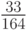1	$- \frac{1777}{4100}$	0	0	$- \frac{341}{164}$	$\frac{4496}{1025}$	$- \frac{289}{82}$	$\frac{2193}{4100}$	$\frac{51}{82}$	$\frac{33}{164}$	$\frac{12}{41}$	0	1
	41/840	0	0	0	0	34/105	9/35	9/35	9/280	9/280	41/840	0	0
	0	0	0	0	0	34/105	9/35	9/35	9/280	9/280	0	41/840	41/840

Таблица 8.16.
$\beta_{ij}$		i
$\beta_{ij}$		2	3	4	5	6	7
j	1	1/18	1/48	1/32	5/16	3/80	$\frac{29 443 841}{614 563 906}$
	2		1/16	0	0	0	0
	3			3/32	- 75/64	0	0
	4				75/64	3/16	$\frac{77 736 538}{692 538 347}$
	5					3/20	$- \frac{28 693 883}{1 112 000 000}$
	6						$\frac{23 124 283 393}{1 800 000 000}$

$\beta_{ij}$		i
$\beta_{ij}$		8	9	10	11	12	13
j	1	$\frac{16 016 141}{946 692 911}$	$\frac{39 632 708}{573 591 083}$	$\frac{246 121 993}{1 340 847 787}$	$- \frac{1 028 468 189}{846 180 014}$	$\frac{185 892 177}{718 116 043}$	$\frac{403 863 854}{491 063 109}$
	2, 3	0	0	0	0	0	0
	4	$\frac{61 564 180}{158 732 637}$	$- \frac{433 636 366}{683 701 615}$	$- \frac{37 695 042 795}{15 268 766 246}$	$\frac{8 478 235 783}{506 512 852}$	$- \frac{3 185 094 517}{667 107 341}$	$- \frac{5 068 492 393}{434 740 067}$
	5	$\frac{22 789 713}{633 445 777}$	$- \frac{421 739 975}{2 616 292 301}$	$- \frac{309 121 744}{1 061 227 803}$	$\frac{1 311 729 495}{1 432 422 823}$	$- \frac{477 755 414}{1 098 053 517}$	$- \frac{411 421 997}{543 043 805}$
	6	$\frac{545 815 736}{2 771 057 229}$	$\frac{100 302 831}{723 423 059}$	$- \frac{12 992 083}{490 766 935}$	$- \frac{10 304 129 995}{1 701 304 382}$	$- \frac{703 635 378}{230 739 211}$	$\frac{652 783 627}{914 296 604}$
	7	$- \frac{180 193 667}{1 043 307 555}$	$\frac{790 204 164}{839 813 087}$	$\frac{6 005 943 433}{2 108 947 869}$	$- \frac{48 777 925 059}{3 047 939 560}$	$\frac{5 731 566 787}{1 027 545 527}$	$\frac{11 173 962 825}{925 320 556}$
	8		$\frac{800 635 310}{3 783 071 287}$	$\frac{393 006 217}{1 396 673 457}$	$\frac{15 336 726 248}{1 032 824 649}$	$\frac{5 232 866 602}{850 066 563}$	$- \frac{13 158 990 841}{6 184 727 034}$
	9			$\frac{123 872 331}{1 001 029 789}$	$- \frac{45 442 868 181}{3 398 467 696}$	$- \frac{4 093 664 535}{808 688 257}$	$\frac{3 936 647 629}{1 978 049 680}$
	10				$\frac{3 065 993 473}{597 172 653}$	$\frac{3 962 137 247}{1 805 957 418}$	$- \frac{160 528 059}{685 178 525}$
	11					$\frac{65 686 385}{487 910 083}$	$\frac{248 638 103}{1 413 531 060}$

Таблица 8.17.
i	1	2	3	4	5	6	7	8
$\alpha_i$	1	$\frac{1}{18}$	$\frac{1}{12}$	$\frac{1}{8}$	$\frac{5}{16}$	$\frac{3}{8}$	$\frac{59}{400}$	$\frac{93}{200}$
$\gamma _{i}$	$\frac{14 005 451}{335 480 064}$	0	0	0	0	$- \frac{59 238 493}{1 068 277 825}$	$\frac{181 606 676}{758 867 731}$	$\frac{561 292 985}{797 845 732}$
$\bar {\gamma}_i$	$\frac{13 451 932}{455 176 623}$	0	0	0	0	$- \frac{808 719 846}{976 000 145}$	$\frac{1 757 004 468}{5 645 159 321}$	$\frac{656 045 339}{265 891 186}$

i	9	10	11	12	13
$\alpha_i$	$\frac{5 490 023 248}{9 719 169 821}$	$\frac{1 201 146 811}{1 299 019 798}$	$\frac{3}{20}$	1	1
$\gamma _{i}$	$- \frac{1 041 891 430}{1 371 343 529}$	$\frac{760 417 239}{1 151 165 299}$	$\frac{118 820 643}{751 138 087}$	$- \frac{528 747 749}{2 220 607 170}$	$\frac{1}{4}$
$\bar {\gamma}_i$	$- \frac{3 867 574 721}{1 518 517 206}$	$\frac{465 885 868}{322 736 535}$	$\frac{5 301 238}{667 516 719}$	$\frac{2}{45}$	0