Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений

Доказательство.

Из полученного в теореме 2 неравенства (8.9) имеем

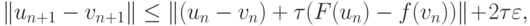
где F(u) — функция приращения метода Рунге - Кутты для систем ОДУ.

Оценим норму разности в правой части неравенства, используя более точные свойства функции F(u), чем Липшиц - непрерывность:

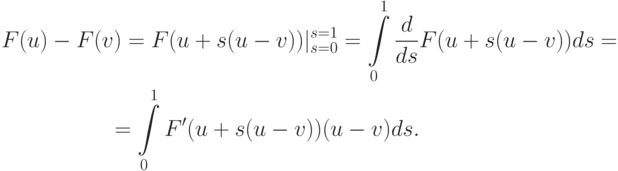
Здесь произведена замена переменных u(s) = v + s(u - v).

Поскольку

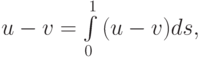
то получаем, что

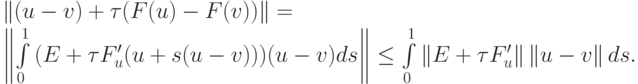( 8.11)

Оценим норму 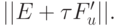Для этого сначала оценим квадрат нормы

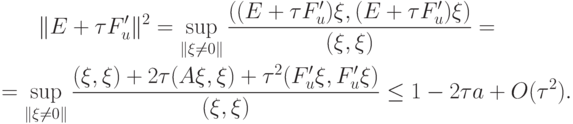
Здесь использовано определение нормы матрицы ( "Численное решение систем линейных алгебраических уравнений" )

где B — матрица, — вектор из рассматриваемого пространства.

При малых 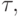пренебрегая членами порядка 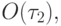из последнего неравенства получаем требуемую оценку:

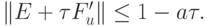
Тогда из (8.11) имеем

откуда

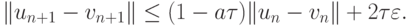
Рассмотрев, как и ранее, цепочку неравенств

получим

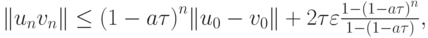
или

( 8.12)

Утверждение доказано.

Пусть теперь 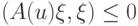т.е. рассматриваются нейтральные, или "не неустойчивые" траектории исследуемой системы обыкновенных дифференциальных уравнений. В этом случае аналогичным образом показывается, что

Тогда, проведя аналогичные выкладки, получим

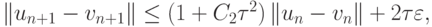
откуда

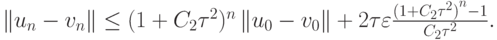
Для метода k - го порядка аппроксимации 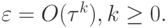В этом случае решения близких систем на n - м шаге по времени отличаются на величину

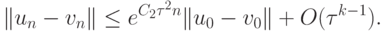( 8.13)

Отсюда видно, что при (или ) численное решение имеет точность Другими словами, на конечных интервалах времени 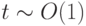точность метода 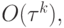на больших же временах точность понижается до

Такие случаи возникают, когда имеется необходимость проводить численные расчеты при исследовании процессов с большим количеством колебаний, вращений и т.д. Важно отметить то, что полученные оценки погрешности численного решения получены с использованием более сильных, чем условие Липшиц - непрерывности, свойств правых частей рассматриваемых дифференциальных уравнений.