НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 9: Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский физико-технический институт

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать программу

8.7. Задачи для самостоятельного решения

Для уравнения Ферхюльста (8.20) рассмотреть неявный метод Эйлера
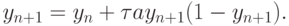
${y_{n + 1} = y_n + {\tau}ay_{n + 1} (1 - y_{n + 1}).}$ ( 8.23)

Для определения y_{n + 1} можно воспользоваться (8.23), решая его как квадратное уравнение. Что можно сказать про устойчивость такого метода? Как правильно выбрать корень квадратного уравнения (8.23)?
Реализовать явный и неявный методы Эйлера и метод Рунге - Кутты порядка аппроксимации 4 для системы уравнений Лотки - Вольтерра "хищник - жертва", которая описывает динамику простейшей экосистемы:
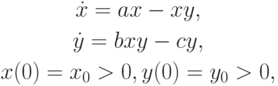
$\begin{gather*} \dot {x} = ax - xy, \\ \dot {y} = bxy - cy, \\ x(0) = x_0 > 0, y(0) = y_0 > 0, \end{gather*}$

Здесь x — безразмерная численность "жертв", y — численность "хищников", a, b, C — положительные константы, b < 1.

Построить графики численных решений на фазовой плоскости (x, y). Построить там же график точного решения. Объяснить полученные результаты. Что будет в случае, когда конечное время, до которого происходит расчет, $T \gg 1$ ?

Построение точного решени в [8.13, с. 36]. На фазовой плоскости точному решению соответствует кривая

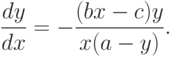
$\frac{{dy}}{{dx}} = - \frac{{(bx - c)y}}{{x(a - y)}}.$

Вводя другую параметризацию кривой y(x), получим, что она может быть описана системой уравнений

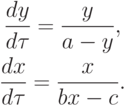
$\begin{gather*} \frac{dy}{d{\tau}} = \frac{y}{a - y}, \\ \frac{dx}{d{\tau}} = \frac{x}{bx - c}. \end{gather*}$

Эта система легко интегрируется, а после исключения параметра $\tau$ находим первый интеграл исходной системы.
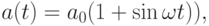
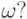
Решить численно систему из предыдущей задачи, когда скорость размножения жертв является периодической функцией времени: $a(t) = a_{0}(1 + \sin \omega t)),$ $\omega$ — параметр. Что происходит с решением при увеличении $\omega?$
Уравнение Ван - дер - Поля [8.3, с. 115 - 119]
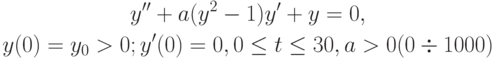
$\begin{gather*} y^{\prime\prime} + a(y^2 - 1)y^{\prime} + y = 0, \\ y(0) = y_0 > 0; y^{\prime} (0) = 0, 0 \le t \le 30, a > 0 (0 \div 1 000) \end{gather*}$

описывает нелинейные колебания в различных системах.
- а) Проинтегрировать уравнение численно явными методами Рунге - Кутты различных порядков. При каких шагах методы становятся неустойчивыми?
  Указание: представить уравнение в виде системы
```
y' = - p, 
p' = ap(y² - 1) + y,
```
  или в виде
  
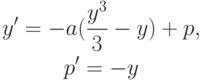
  $\begin{gather*} y^{\prime} = - a(\frac{{y^3 }}{3} - y) + p, \\ p^{\prime} = - y \end{gather*}$
  
  (представление Льенара).
- б) Реализовать для уравнения Ван - дер - Поля следующие полуявные методы Рунге - Кутты:
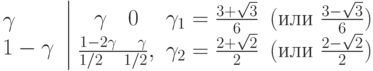
  $\left. \begin{array}{l} \gamma \\ {1 - \gamma} \\ \end{array} \right. \left| \begin{array}{ccc} \gamma \quad 0 & \gamma_1 = \frac{3 + \sqrt{3}}{6} & (\mbox{или } \frac{3 - \sqrt{3}}{6}) \\ \frac{1 - 2\gamma \quad \gamma}{1/2 \quad 1/2}, & \gamma_2 = \frac{2 + \sqrt{2}}{2} & (\mbox{или } \frac{2 - \sqrt{2}}{2}) \\ \end{array} \right.$
  
  Какой порядок аппроксимации они имеют? Устойчивы ли они?
Уравнение Эйлера
Решить численно задачу о колебаниях в системе, где и возвращающая сила, и коэффициент вязкого трения убывают со временем (уравнение Эйлера):

$\ddot {x} + \frac{\dot {x}}{t} + 100\frac{x}{t^2 } = 0,$

где $t \in [1, 100], x (1) = 1, \dot {x}(1) = 1.$

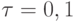
Использовать для численного решения сетки с шагом $\tau = 0, 1$
- а) явный метод Эйлера;
- б) неявный метод Эйлера;
- в) методы Рунге - Кутты порядка 2, 3, 4.
Уменьшить $\tau$ вдвое. Что происходит с решением? Какому решению верить?

Сравнить численное решение с точным.

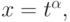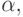Указание. Будем искать точное решение в виде $x = t^{\alpha},$ где $\alpha,$ вообще говоря, комплексное. Рекомендации можно найти в [8.14].
Уравнение Эйлера
Рассмотрим более простую систему без трения:

$\ddot {x} + 100\frac{x}{t^2 } = 0.$

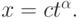
Выполнить пункты предыдущей задачи. В чем заключается разница? Точное решение уравнения можно найти в [8.14] или решить уравнение самостоятельно, положив $x = ct^{\alpha}.$
Уравнение Хатчинсона
Одной из модификаций уравнений Ферхюльста является уравнение Ферхюльста с запаздыванием (уравнение Хатчинсона):

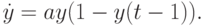
Заметим, что в качестве начальных условий необходимо задавать y(t) при $t \in [- 1, 0],$ т.е. не в одной точке, а на отрезке.
- а) Аналитически решить уравнение так называемым методом шагов. Задавая конкретную функцию y(t) = g(t) при $t \in [- 1, 0]$ (начальные условия), интегрируем уравнение Хатчинсона на полуинтервале при $t \in ]0, 1]$ :
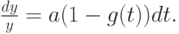
  $\frac{dy}{y} = a(1 - g(t)) dt.$
  
  Зная y(t) на [0, 1], можно найти y(t) на [1, 2] и т.д.
  
  Если положить y(t) = 1/2 при $t \in ] - 1, 0],$ y(t) = t , y(t) = e^{- t}, что происходит в точках t = 1, 2, 3, ... n, ...?
- б) Построить численный метод интегрирования уравнение Хатчинсона. Найти решение в случае
  $y(t) = e^{- t^2 }, t \in [- 1, 0]$
  
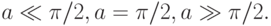
  при $a \ll \pi/2, a = \pi/2, a \gg \pi/2.$
  
  О численном решении уравнений с запаздыванием [8.3, с. 304 - 319].
Уравнение Минорского
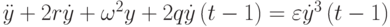
$\ddot {y} + 2r\dot {y} + \omega ^2 y + 2q\dot {y}\left({t - 1}\right) = \varepsilon \dot {y}^3 \left({t - 1}\right)$

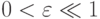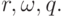встречается в различных механических и электротехнических задачах, в которых имеется запаздывание и нелинейность (здесь $r, \omega , q$ — постоянные, $0 < \varepsilon \ll 1$ ). Построить численное решение, задавая начальные данные на отрезке $t \in [- 1, 0].$ Рассмотреть зависимость решения от параметров $r, \omega , q.$ В качестве одного из характерных случаев значений этих параметров рассмотреть следующие: r = - 1, q = (- 1)n,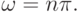 $\omega = n\pi.$

Подробное качественное исследование уравнения Минорского представлено в [8.12, с. 191 - 211].
Уравнение Тинбергена
$\dot {y} + by(t - 1) = \varepsilon [y(t - 1)]^3, \quad 0 < \varepsilon \ll 1$

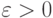получено при исследовании циклов в судостроительной промышленности. Предполагается, что время постройки одного судна постоянно (и принято за единицу). Превышение темпа закладки новых судов над средним теоретическим темпом закладки пропорционально нелинейной функции $y - (\varepsilon /b)y^{3}.$ Для рассматриваемого случая $\varepsilon > 0$ уравнение показывает, что при возрастании отклонения судостроители должны реагировать относительно более консервативно из - за недостатка материалов, рабочей силы и т.п. 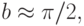Решить уравнение численно, задавая начальные данные на отрезке $t \in [- 1, 0].$ Рассмотреть характерные режимы: 1) 0 < b < 1/e, 2) $b \approx \pi /2,$ 3) $b > \pi /2.$

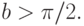
Показать, что в интервале $0 < b < \pi /2$ решение уравнения ведет себя так же, как решение линейного уравнения ( $\varepsilon = 0$ ). Исследование поведения решения уравнения Тинбергена имеется в [8.12, с. 180 - 184].