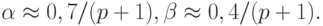Введение в вычислительную математику

:

Введение в вычислительную математику
[+]
Опубликован: 25.10.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский физико-технический институт
Лекция 9:

Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений
A
|
версия для печати
< Лекция 8 || Лекция 9: 1234567891011 || Лекция 10 >

8.4. Оценка погрешности

8.4.1. Автоматический выбор шага интегрирования

Рунге предложил простое правило оценки точности метода, основанное на проведении вычислений с разными шагами интегрирования. Основная идея правила Рунге заключается в следующем.

Погрешность численного метода порядка p - 1 в точке t_{i} = i\tau представляется в виде

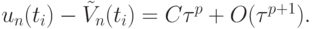
u_n (t_i) - \tilde V_n (t_i) = C {\tau}^{p} + O({\tau}^{p + 1}).

Если выполнить аналогичные вычисления с шагом вдвое меньшим, 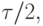\tau /2, то получим

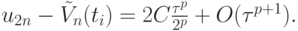
$ u_{2n} - \tilde V_n (t_i) = 2C \frac{{\tau}^p}{2^p} + O({\tau}^{p + 1}). $

После вычитания из первого соотношения второго

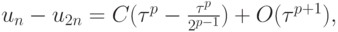
$ u_n - u_{2n} = C ({\tau}^{p} - \frac{{\tau}^p}{2^{p - 1}}) + O({\tau}^{p + 1}), $

откуда

$ C = \frac{2^{p - 1}}{{\tau}^{p}} \frac{u_n - u_{2n}}{2^{p - 1} - 1} + O ({\tau}). $

Подставив выражение для C во второе соотношение, получим

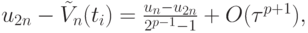
$ u_{2n} - \tilde V_n (t_i) = \frac{{u_n - u_{2n}}}{{2^{p - 1} - 1}} + O({\tau}^{p + 1}), $

т.е. погрешность метода, с точностью 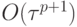O(\tau ^{p + 1}) оценивается по простой формуле

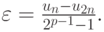
$ \varepsilon = \frac{u_n - u_{2n}}{2^{p - 1} - 1}. $

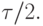Это правило используется не только для оценки погрешности вычисления, но и для автоматического выбора шага интегрирования. Для этого на каждом шаге вычисления производятся трижды: с шагом \tau и с двумя шагами \tau /2. Полученные значения un и u2n используются для вычисления реальной погрешности \varepsilon (точнее, оценки ее главного члена). 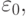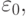Если величина \varepsilon превышает некую заданную (или заранее выбранную) константу \varepsilon _{0}, то шаг интегрирования уменьшается; если, напротив, \varepsilon существенно меньше \varepsilon _{0}, то \tau увеличивается.

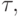Разумеется, алгоритмы выбора шага интегрирования могут основываться и на иных принципах. Например, можно выбрать \tau адаптирующимся к решению: уменьшать при увеличении абсолютной величины производной и увеличивать при ее уменьшении, т.е. вычислять \tau, как функцию от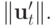 \|\mathbf{u}^{\prime}_{t}\|.

Управление длиной шага в методах Рунге - Кутты осуществляется на основе сравнения с некоторой задаваемой величиной T, характеризующей требования к погрешности на каждом шаге численного интегрирования системы.

Пусть используется метод с порядком аппроксимации p. Тогда главный член погрешности метода 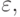\varepsilon, определяемый по правилу Рунге, или, в случае использования вложенных методов Рунге - Кутты, представляющий собой модуль разности между приближениями к решению, вычисленными по формулам (8.5) и (8.6), имеет вид

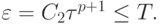
\varepsilon = C_2 {\tau}^{p + 1} \le T.

Положим теперь T = C_2 {\tau}_{new}^{p + 1}. Тогда для величины максимального значения нового шага интегрирования \tau _{new} получаем

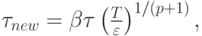
$ {\tau}_{new} = \beta {\tau}\left({\frac{T}{\varepsilon }}\right)^{1/(p + 1)}, $

где \beta — так называемый гарантированный множитель. Он служит для того, чтобы в случае резкого уменьшения шага (например, при выходе на жесткий участок при решении умеренно жестких систем ) численный метод оставался устойчивым.

Кроме того, гарантированный множитель помогает избежать слишком быстрого увеличения величины шага интегрирования в случае, когда реально полученная погрешность мала. Обычно величина гарантийного множителя принимается за 0, 5; 0, 8; 0, 9 или 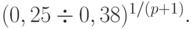(0, 25 \div 0, 38)^{1/(p + 1)}.

Если при выполнении очередного шага погрешность \varepsilon не превосходит величины T, то шаг считается принятым, а дальнейший расчет продолжается с шагом \tau _{new}, в противном случае шаг считается отклоненным, и проводится пересчет с новым значением шага для перехода от tn к tn + 1.

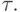На практике применяют модернизации алгоритма выбора шага. Так, если реальная ошибка \varepsilon мала, то предлагаемый алгоритм позволяет выбрать очень большой шаг по \tau. В таком случае применяют алгоритм

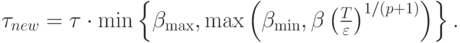
$ {\tau}_{new} = {\tau}\cdot \min \left\{{\beta_{\max }, \max \left({\beta_{\min }, \beta \left({\frac{T}{\varepsilon }}\right)^{1/(p + 1)}}\right)}\right\}. $

Здесь 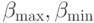\beta_{\max }, \beta_{\min } — максимальное и минимальное разрешенное изменение шага интегрирования.

Другая возможность регулировки шага численного интегрирования для методов Рунге - Кутты заключается в объединении достоинств методов Рунге - Кутты и Адамса. Первые из них допускают легко регулировать шаг интегрирования, а вторые помнят часть предыстории изменения функции.

Более тонкий алгоритм управления величиной шага получается с учетом величины ошибки на предыдущем шаге

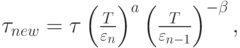
$ {\tau}_{new} = {\tau}\left({\frac{T}{\varepsilon_n}}\right)^{a} \left({\frac{T}{{\varepsilon_{n - 1}}}}\right)^{- \beta }, $

т.е. фактически гарантийный множитель зависит от ошибки на предыдущем шаге. Обычно при таком выборе управления длиной шага полагается 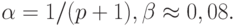\alpha = 1/(p + 1), \beta \approx 0, 08 .

Такой выбор регулировки шага повышает устойчивость численных методов Рунге - Кутты не очень высокого порядка. Для метода Дормана - Принса порядка 8(7) лучшие результаты дает 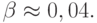\beta \approx 0, 04 .

В [8.10] показано, что такой метод выбора шага является решением задачи оптимального управления с учетом пропорциональной обратной связи и интегральной обратной связи. Там же показано, что оптимальный выбор показателей степени есть \alpha \approx 0, 7/(p + 1), \beta \approx 0, 4/(p + 1).

Дальше >>
< Лекция 8 || Лекция 9: 1234567891011 || Лекция 10 >

Вопросы и ответы

вопросов: 1
Sanjar Ibrohimov
Sanjar Ibrohimov
ответить

Студенты

всего: 131
Эдуард Макаров
Эдуард Макаров
Россия, Челябинск, Челябинский политехнический институт, 1966
предложить дружбу
Иван Кузнецов
Иван Кузнецов
Россия, г. Новосибирск
предложить дружбу