НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 9: Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский физико-технический институт

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать программу

8.6. Задачи

Семейство явных методов Рунге - Кутты
Пусть дана следующая система обыкновенных дифференциальных уравнений:

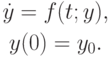
$\begin{gather*} \dot {y} = f(t;y), \\ y(0) = y_0 . \end{gather*}$

Для численного решения задачи проведем следующие вычисления:

$\begin{gather*} k_1 = f(t_n, y_n), \\ k_2 = f(t_n + c_2 {\tau}, y_n + {\tau}b_{21}k_1 ), \\ k_{s} = f(t_n + c_{s} {\tau}, y_n + {\tau}\sum\limits_{r = 1}^{s - 1}{b_{sr}k_r}), \\ y_{n + 1} = y_n + {\tau}\sum\limits_{p = 1}^s{a_p k_p}, \end{gather*}$

где a, b, C — действительные числа (вектор y_n считается известным, т.к. y₀ — начальные условия, по этим значениям можно найти y₁ и т.д.).

Численный метод называется явным методом Рунге - Кутты порядка S или S - стадийным.

Будем также записывать метод Рунге - Кутты в виде таблицы Бутчера — таблицы коэффициентов метода:

0 0 0 $\ldots$ 0 0

C₂ b₂₁ 0 $\ldots$ 0 0

$\ldots$ $\ldots$ $\ldots$ $\ldots$ $\ldots$ $\ldots$

c_s b_s1 b_s2 $\ldots$ b_{ss - 1} 0

a₁ a₂ $\ldots$ a_{s - 1} a_s

Для метода порядка S вывести условия, связывающие коэффициенты таблицы Бутчера, необходимые для обеспечения p - го порядка аппроксимации метода ( $p \le s$ ).

Указание 1. Разложить проекцию на сетку точного решения задачи Коши в ряд Тейлора в окрестности точки t_n. Использовать следствия исходного дифференциального уравнения, например:

$\frac{d^2 y}{d t^2 } = \frac{d}{dt}f(t, y) = \frac{\partial f}{\partial t} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial t} = \frac{\partial f}{\partial t} + \frac{\partial f}{\partial y}f.$

Указание 2. Для простоты все вычисления провести для случая одного нелинейного уравнения. Требуемые условия приведены в [8.3, с. 153, 162]. В качестве упражнения найти все явные методы Рунге - Кутты с S = p = 3, S = p = 4.
Семейство неявных методов Рунге - Кутты
Метод вида

$\begin{gather*} k_1 = f(t_n + c_1 {\tau}, y_n + {\tau}\sum\limits_{l = 1}^{s}{b_{1l}k_l} ), \\ \ldots \\ k_{s} = f(t_n + c_{s} {\tau}, y_n + {\tau}\sum\limits_{l = 1}^{s}{b_{sl}k_l}), \\ y_{n + 1} = y_n + {\tau}\sum\limits_{l = 1}^{s}{a_l k_l}, \end{gather*}$

где k₁, ..., k_s определяются как решение нелинейной системы уравнений, называется неявным методом Рунге - Кутты порядка S ( S - стадийным ). Как будет выглядеть для него таблица Бутчера?

Вывести условия аппроксимации порядка p на решении ( p = 1, 2, 3, 4 ; S = 2 ).

Следует обратить внимание на то, что для определения k₁, k₂, , k_s необходимо решать систему нелинейных уравнений. Какова ее размерность?

В чем состоит особенность методов с b_ij = 0 при j > i?

(Это так называемые полуявные или диагонально - неявные методы).
Управление длиной шага
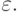
- a) Система ОДУ решается с помощью метода Рунге - Кутты порядка аппроксимации p > 1. Описать алгоритм выбора шагов интегрирования, таких, чтобы достигнутая погрешность на каждом из них не превосходила заданную величину $\varepsilon.$
  Решение. Пусть переход от значения y_n к y_{n + 1} осуществляется с шагом h. Тогда в результате работы метода получим
  
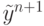  ${y^{n + 1} = \tilde {y}^{n + 1} + Ch^{p + 1} + O(h^{{p} + 2}), }$ ( 8.14)
  
  где $\tilde {y}^{n + 1}$ — точное решение задачи, взятое в точке n + 1, Ch^{p + 1} — главный член погрешности, постоянная C зависит как от коэффициентов конкретного метода, так и от решения задачи. (Из решения задачи 8.1 следует, что разложения y_{n + 1} и $\tilde {y}^{n + 1}$ в ряд Тейлора совпадают до членов с номерами p + 1 включительно).
  
  Осуществим теперь переход от y_n к y_{n + 1} за два этапа, используя тот же метод Рунге - Кутты с шагом h/2. Тогда имеем
  
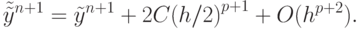
  $\tilde {\tilde {y}}^{n + 1} = \tilde {y}^{n + 1} + 2C{(h/2)}^{p + 1} + O(h^{p + 2}).}$ ( 8.15)
  
  Так как C оценивается через максимальное по абсолютной величине значение (p + 1) - й производной на отрезке [t_n, t_{n + 1}], можно считать, что в последнем выражении константа совпадает с константой в предыдущем равенстве. Используя два равенства, возможно либо явно вычислить Ch^p и исключить его из (8.15), повысив точность аппроксимации на порядок, либо поступить следующим образом. Вычитая из (8.15) равенство (8.14), имеем
  
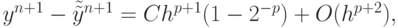
  $y^{n + 1} - \tilde {\tilde {y}}^{n + 1} = Ch^{p + 1} (1 - 2^{- p}) + O(h^{p + 2}),$
  отсюда главный член погрешности (8.15) будет равен
  
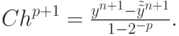
  ${Ch}^{p + 1} = \frac{{y^{n + 1} - \tilde {\tilde {y}}^{n + 1}}}{{1 - 2^{- p}}}.}$ ( 8.16)
  
  Необходимо выбрать шаг интегрирования h_new таким образом, чтобы главный член погрешности не превосходил заданное значение $(Ch}_{new}^{p + 1} < \varepsilon )$ :
  
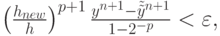
  $\left({\frac{{h_{new}}}{h}}\right)^{p + 1} \frac{{y^{{n} + 1} - \tilde {\tilde {y}}^{n + 1}}}{{1 - 2^{- {p}}}} < \varepsilon ,$
  
  откуда имеем
  
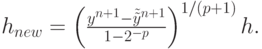
  ${h_{new} = \left({\frac{{y^{n + 1} - \tilde {\tilde {y}}^{n + 1}}}{{1 - 2^{- {p}}}}}\right)^{1/(p + 1)}h. }$ ( 8.17)
  
  Если же на текущем шаге погрешность (8.16) превышает 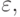$\varepsilon,$ то шаг считается отклоненным и расчет выполняется снова со значением, найденным по формуле (8.17).
- б) Система ОДУ решается с помощью явных методов p и p + 1 порядка аппроксимации. На каждом шаге погрешность расчетов не должна превышать 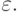$\varepsilon.$ Как выбрать длину шага интегрирования?
  Рассуждаем аналогично тому, как это сделано в пункте 1. При расчете методом p порядка аппроксимации имеем
  
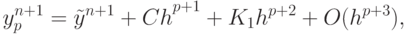
  ${y_p^{n + 1} = \tilde {y}^{n + 1} + Ch}^{p + 1} + K_1 h^{{p} + 2} + O(h^{p + 3}), }$ ( 8.18)
  
  а p + 1 порядок дает
  
  ${y_{p + 1}^{n + 1} = \tilde {y}^{n + 1} + K_2 h^{{p} + 2} + O(h^{{p} + 3}).}$ ( 8.19)
  
  Отсюда сразу получаем 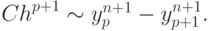${Ch}^{p + 1} \sim y_p^{n + 1} - y_{p + 1}^{n + 1} .$ Эти величины сравниваются с заданной точностью.
  
  Существует семейство методов Рунге - Кутты, таких, что члены погрешности для результата старшего ( p + 1 ) порядка минимизируются, а вычисление погрешности p - го порядка используется лишь для управления длиной шага. При этом для порядка p и p + 1 коэффициенты b, c в таблице Бутчера (2.4.1) совпадают, а различаются лишь коэффициенты a. Кроме того, b_si = a_i(y_p). Такие методы построены Дорманом и Принсом и носят их имя.
Рассмотрим уравнение Ферхюльста (логистическое уравнение) , описывающее динамику численности популяции:
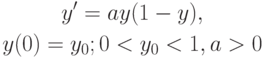
$\begin{gather*} {y^{\prime} = ay(1 - y), } \\ y(0) = y_0; 0 < y_0 < 1, a > 0 \end{gather*}$ ( 8.20)
- а) Решить уравнение (8.20) точно, учитывая, что это уравнение в разделяющихся переменных. Получившаяся кривая — график точного решения — носит название логистической кривой.
- б) Рассмотреть для (8.20) явный метод Эйлера:
  ${y_{n + 1} = y_n + {\tau}ay_n \left({1 - y_n}\right).}$ ( 8.21)
  
  При каких шагах $\tau$ метод является устойчивым?
  
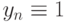  Решение. При $t \longrightarrow \infty$ точное решение (8.20) асимптотически стремится к единице. Очевидно, что последовательность $y_n \equiv 1$ является и решением (8.20). Непосредственно проверяется, что (8.21) аппроксимирует (8.20) с точностью $O(\tau ).$ В случае, если метод (8.21) устойчив , то решение (8.21) сходится к решению (8.20) и должно выполняться неравенство
```
| y_{n + 1} - 1 | < | y_n - 1 | .
```
  Если рассмотреть (8.21) как запись метода простых итераций для (8.20), то он должен сходиться к корню y = 1 при любом начальном приближении y₀, лежащем между 0 и 1.
  
  Перепишем (8.21) в виде
  
  ${z_{n + 1} = bz_n (1 - z_n), z_n = \frac{{{\tau}a}}{{{\tau}a + 1}}y_n; b= 1 + {\tau}a}$ ( 8.22)
  
  и для (8.22) воспользуемся результатами, полученными в "Численное решение нелинейных алгебраических уравнений и систем" . Таким образом, условия устойчивости для (8.21) будут следующими:
  
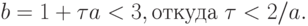
  $b = 1 + \tau a < 3, откуда \ \tau < 2/a.$
- с) Описать сценарий развития вычислительной неустойчивости для задачи (8.21), можно воспользоваться материалом "Численное решение нелинейных алгебраических уравнений и систем" . Следует обратить внимание на то, что когда метод неустойчив, в отличие от линейных задач, модуль разности численного и точного решений остается ограниченным при любом сколь угодно большом t при ${2/a} \le {\tau}< {3/a}.$