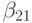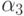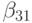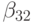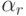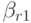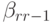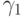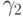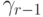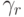НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 9: Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский физико-технический институт

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать программу

8.2. Методы Рунге - Кутты

Наиболее распространенными при численном решении обыкновенных дифференциальных уравнений являются методы Рунге - Кутты. Их принято представлять в следующей форме [8.3].

Определение. r - шаговый явный метод для численного решения задачи Коши для обыкновенного дифференциального уравнения (8.1):

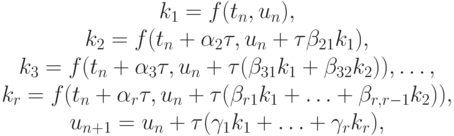$\left. \begin{array}{c} k_1 = f(t_n, u_n), \\ k_2 = f(t_n + \alpha_2 {\tau}, u_n + {\tau}\beta_{21} k_1 ), \\ {k_3 = f(t_n + \alpha_3 {\tau}, u_n + {\tau}(\beta_{31}k_1 + \beta_{32} k_2 )), \ldots , }\\ k_r = f(t_n + \alpha_r {\tau}, u_n + {\tau}(\beta_{r1} k_1 + \ldots + \beta_{r, r - 1} k_2 )), \\ u_{n + 1} = u_n + {\tau}(\gamma_1 k_1 + \ldots + \gamma_r k_r), \end{array} \right.$

( 8.4)

где k_i — промежуточные вспомогательные величины.

Коэффициенты, определяющие конкретный метод, могут быть представлены в виде таблицы Бутчера (табл. 8.1). Нулевые коэффициенты $\beta_{ij} ,$ как правило, в таблице Бутчера не указывают.

Таблица 8.1.
0
$\alpha_2$	$\beta_{21}$
$\alpha_3$	$\beta_{31}$	$\beta_{32}$
$\ldots$	$\ldots$	$\ldots$	$\ldots$
$\alpha_r$	$\beta_{r1}$	$\beta_{r2}$	$\ldots$	$\beta_{rr - 1}$
	$\gamma_1$	$\gamma_2$	$\ldots$	$\gamma_{r - 1}$	$\gamma_r$

Обычно также используют условие, предложенное Куттой без объяснений и не являющееся обязательным [8.3]:

$\alpha_n = \sum\limits_j{\beta_{nj}}.$

Получим простейшие методы Рунге - Кутты. Для этого введем погрешность

$\xi ({\tau}) = u(t + {\tau}) - \left[{u(t) + \sum\limits_{j = 0}^{r}{\gamma_j k_j} }\right]$

и представим ее в виде разложения в ряд Маклорена

$\xi ({\tau}) = \sum\limits_{i = 0}^{p}\frac{\xi^{(i)}(0)}{i!} {\tau}^{i} + \frac{\xi^{(p + 1)}(\theta{\tau})}{(p + 1)!} {\tau}^{p + 1},$

где

$\frac{\xi^{(p + 1)}(\theta{\tau})}{(p + 1)!} \tau^{p + 1}$

— остаточный член ряда; $0 < \theta < 1.$

Будем полагать (что можно сделать соответствующим выбором коэффициентов)

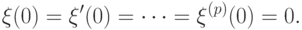
$\xi (0) = \xi '(0) = \dots = \xi ^{(p)}(0) = 0.$

В таком случае разложение для $\xi (\tau )$ имеет более простой вид:

$\xi ({\tau}) = \frac{\xi^{(p + 1)}(\theta{\tau})}{(p + 1)!} {\tau}^{p + 1},$

где p — порядок точности метода.

Пусть p = 1, r = 1. Тогда
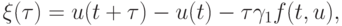
$\xi (\tau ) = u(t + \tau ) - u(t) - \tau \gamma _{1} f(t, u),$

отсюда

$\begin{gather*} \xi (0) = 0, \\ {\xi}^{\prime}(0) \equiv \left. {[u^{\prime}(t + {\tau}) - \gamma_1 f(t, u)]}\right|_{t = 0} = f(t, u) (1 - \gamma_1 ), \\ {\xi}^{\prime\prime}(0) = u^{\prime\prime}(t + {\tau}). \end{gather*}$

Видно, что условие $\xi (0) = 0$ выполняется лишь при $\gamma _{1} = 0,$ что соответствует методу Эйлера, при этом

$\frac{u(t + {\tau}) - u(t)}{{\tau}} - f(t, u) = \frac{{\xi}^{\prime\prime}(t + \theta{\tau})}{2} {\tau}= R_{\tau},$

где $R_{\tau }$ — невязка, имеющая первый порядок малости по $\tau.$
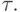
Рассмотрим более сложный случай: p = 2, r = 2. Тогда
$\xi ({\tau}) = u (t + {\tau}) - u(t) - {\tau}\gamma_1f(t, u) - {\tau}\gamma_2f(t + \alpha_2{\tau}, u + \beta_{21}{\tau}f(t, u)).$

Вводя обозначения

получим следующие выражения для производных погрешности $\xi$ по аргументу $\tau:$

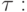
$\begin{gather*} \xi^{\prime}({\tau}) = u^{\prime}(t + {\tau}) - \gamma_1f(t, u) - \gamma_2f(\tilde{t}, \tilde{u}) - \\ - {\tau}\gamma_2[\alpha_2f^{\prime}_{t}(\tilde{t}, \tilde{u}) + \beta_{21}f^{\prime}_u(\tilde{t}, \tilde{u})f(t, u)], \\ {\xi}^{\prime\prime}({\tau}) = u^{\prime\prime}(t + {\tau}) - 2\gamma_2 [\alpha_2 f^{\prime}_{t} (\tilde {t}, \tilde {u}) + \beta_{21} f^{\prime}_u (\tilde {t}, \tilde {u}) f(t, {u})] - \\ - {\tau}\gamma_2[\alpha_2^2f^{\prime\prime}_{tt}(\tilde{t}, \tilde{u}) + 2\alpha_2\beta_{21} f^{\prime\prime}_{tu}(\tilde{t}, \tilde{u})f(t, u) + \beta^2_{21}f^{\prime\prime}_{uu}(\tilde{t}, \tilde{u})f^2(t, u)], \\ {\xi}^{\prime\prime\prime}({\tau}) = u^{\prime\prime}(t + {\tau}) - 3\gamma_2[\alpha_2^2f^{\prime\prime}_{tt}(\tilde{t}, \tilde{u}) + 2\alpha_2\beta_{21}f^{\prime\prime}_{tu}(\tilde{t}, \tilde{u})f(t, u) + \\ + \beta^2_{21}f^{\prime\prime}_{uu}(\tilde{t}, \tilde{u})f(t, u)] + o({\tau}). \end{gather*}$

Поставив в эти выражения следующие равенства:
```
u' = f, u'' = f'_t + f'_u f, 
u''' = f''_tt + 2f''_tu f + f''_uuf² + f'_u u'',
```
получим

$\begin{gather*} \xi (0) = 0, \xi ^{\prime}(0) = (1 - \gamma_1 - \gamma_2 ) f(t, u), \\ {\xi}^{\prime\prime}(0) = (1 - 2\gamma_2 \alpha_2 ) f^{\prime}_{t} (t, u) + (1 - 2\gamma_2 \beta_{21}) f^{\prime}_u (t, u) f(t, u), \\ {\xi}^{\prime\prime\prime} (0) = (1 - 3\gamma_2\alpha^2_2)f^{\prime\prime}_{tt}(t, u) + (2 - 6\gamma_2\alpha_2\beta_{21})f^{\prime\prime}_{tu}(t, u)f(t, u) + \\ + (1 - 3\gamma_2 \beta_{21}^2 ) f^{\prime\prime}_{uu} (t, u)f^2 (t, u) + f^{\prime}_u (t, u) u^{\prime\prime}(t). \end{gather*}$

Второе из полученных соотношений выполняется при $\gamma _{1} + \gamma _{2} = 1,$ третье — при $1 - 2\gamma_2 \alpha_2 = 0, 1 - 2\gamma_2 \beta_{21} = 0.$

Таким образом, имеется три алгебраических уравнения и четыре параметра. Эти уравнения определяют однопараметрическое семейство схем. Задавая один из параметров, можно получать различные методы Рунге - Кутты с аппроксимацией второго порядка. При формально одинаковом порядке аппроксимации они будут обладать различными свойствами ( устойчивостью, реальной погрешностью).

Так, при $\gamma _{1} = 1/2,$ имеем $\gamma_2 = 1/2, \alpha_2 = 1, \beta_{21} = 1$ ; метод будет выглядеть следующим образом:

$\begin{gather*} \tilde u_{n + 1} = u_n + {\tau}f(t_n, u_n), \\ u_{n + 1} = u_n + \frac{{\tau}}{2} [f(t_n, u_n) + f(t_{n + 1}, \tilde u_{n + 1})]. \end{gather*}$

Положив $\gamma _{1} = 0,$ имеем $\gamma_2 = 1, \alpha_2 = 1/2, \beta_{21} = 1/2$ ; соответствующий метод будет:

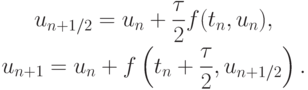
$\begin{gather*} u_{n + 1/2} = u_n + \frac{{\tau}}{2} f(t_n, u_n), \\ u_{n + 1} = u_n + f\left({t_n + \frac{{\tau}}{2}, u_{n + 1/2}}\right). \end{gather*}$
При p = 2, r = 3 получаем систему уравнений для коэффициентов:
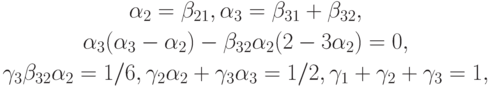
$\begin{gather*} \alpha_2 = \beta_{21}, \alpha_3 = \beta_{31} + \beta_{32}, \\ \alpha_3 (\alpha_3 - \alpha_2 ) - \beta_{32}\alpha_2 (2 - 3\alpha_2 ) = 0, \\ \gamma_3 \beta_{32} \alpha_2 = 1/6, \gamma_2 \alpha_2 + \gamma_3 \alpha_3 = 1/2, \gamma_1 + \gamma_2 + \gamma_3 = 1, \end{gather*}$

имеющую бесконечное множество решений. Расчетные формулы одного из возможных методов имеют вид

$\begin{gather*} k_1 = {\tau}f(t_n, u_n), k_2 = {\tau}f\left({t_n + \frac{{\tau}}{2}, u_n + \frac{{k_1 }}{2}}\right),\\ k_3 = {\tau}f(t_n + {\tau}, u_n - k_1 + 2k_2 ), \\ u_{n + 1} = u_n + \frac{{k_1 + 4k_2 + k_3 }}{6}. \end{gather*}$
В случае p = 4, r = 4 имеем двухпараметрическое семейство методов Рунге - Кутты, из которого наиболее известен следующий "классический" метод:
$\begin{gather*} k_1 = {\tau}f(t_n, u_n), k_2 = {\tau}f\left({t_n + \frac{{\tau}}{2}, u_n + \frac{{k_1 }}{2}}\right),\\ k_3 = {\tau}f\left({t_n + \frac{{\tau}}{2}, u_n + \frac{{k_2 }}{2}}\right), \\ k_4 = {\tau}f(t_n + {\tau}, u_n + k_3 ), \\ u_{n + 1} = u_n + \frac{{k_1 + 2k_2 + 2k_3 + k_4 }}{6}. \end{gather*}$

В представлении Бутчера хорошо известные методы численного решения ОДУ выглядят следующим образом. Метод Эйлера (первый порядок аппроксимации ) табл. 8.2, метод Эйлера с пересчетом (второй порядок аппроксимации ) — табл. 8.3. Метод Хойна третьего порядка аппроксимации — табл. 8.4. Метод Рунге - Кутты третьего порядка аппроксимации — табл. 8.5.

Таблица 8.2.
0	0
	1

Таблица 8.3.
0
1/2	1/2
	0	1

Таблица 8.4.
0
1/3	1/3
2/3	0	2/3
	1/4	0	3/4

Таблица 8.5.
0
1/2	1/2
1	0	1
	1/6	2/3	1/6

Дальше >>

Введение в вычислительную математику

Введение в вычислительную математику

Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений

8.2. Методы Рунге - Кутты

Вопросы и ответы

Студенты

Авторизоваться

Введение в вычислительную математику

Введение в вычислительную математику

Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений

8.2. Методы Рунге - Кутты

Вопросы и ответы

Студенты