| подавляющее большиство фукций на пространстве последовательостей? |
Проект "Выпуклая оболочка"
Этот параграф посвящен, прежде всего, решению одной конкретной задачи средней степени сложности — нахождению выпуклой оболочки последовательно поступающих точек плоскости и вычислению двух ее метрических характеристик. Дополнительная информация об этом проекте может быть найдена в книге [9].
В нем также рассматриваются аплеты, которые используются в качестве основы для создания простейшего графического интерфейса (GUI — graphics user interface), что дает возможность решать задачи на изображение графиков функций и различных графических объектов. Вопросы создания аплетов обсуждаются практически во всех изданиях, посвященных языку Java, в том числе и в книгах [10], [11] и [13].
Постановка задачи
Напомним сначала два определения, связанные с важнейшим математическим понятием — свойством выпуклости множеств.
Определение 11.1.
Множество  называется выпуклым, если для любых двух его
точек
весь отрезок прямой, соединяющий эти точки, принадлежит множеству:
называется выпуклым, если для любых двух его
точек
весь отрезок прямой, соединяющий эти точки, принадлежит множеству: ![M\ \text{выпукло} \Longleftrightarrow (\forall x_1, x_2 \in
M\ [x_1,x_2]\in M)](/sites/default/files/tex_cache/9b48c2de567b32e66bba9dca46e69cab.png) .
.
Примеры выпуклых множеств: отрезок прямой, прямоугольник и круг на плоскости, куб, шар и пирамида в пространстве. Выпуклыми множествами не являются окружность, граница квадрата и тор (прямое произведение двух окружностей).
Определение 11.2. Выпуклой оболочкой 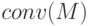 множества
множества  называется наименьшее
выпуклое множество, содержащее
называется наименьшее
выпуклое множество, содержащее  .
.
Выпуклая оболочка любого выпуклого множества совпадает с ним. Для произвольного множества выпуклая оболочка может быть получена как пересечение всех выпуклых множеств, его содержащих.
Выпуклой оболочкой двух точек на плоскости является отрезок, их соединяющий; выпуклая оболочка окружности — круг; выпуклая оболочка трех точек, не лежащих на одной прямой, — треугольник.
Теперь можно сформулировать основную задачу.
Задача 11.1. Напишите программу, находящую выпуклую оболочку последовательно поступающих точек плоскости и вычисляющую ее периметр и площадь. Решение должно быть индуктивным, что означает определение выпуклой оболочки и вычисление ее характеристик сразу после поступления очередной точки с использованием методов теории индуктивных функций.
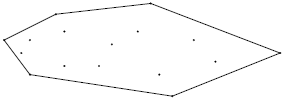
Если представить себе точки конечного множества в виде вбитых в доску гвоздей, то выпуклая оболочка — это многоугольник, форму которого принимает натянутое на гвозди резиновое кольцо (см. рис. 11.1).
Мы будем трактовать поставленную задачу следующим образом: реализовать класс Convex с методами
- add — добавить новую точку и построить выпуклую оболочку;
- perimeter — вычислить периметр;
- area — вычислить площадь.
Договоримся придерживаться стратегии вычисления всех характеристик оболочки сразу при добавлении новой точки (в методе add ); выполнение методов perimeter и area при этом будет сводиться просто к выдаче уже вычисленных ранее значений.
Если обозначить множество  точек плоскости через
точек плоскости через  , а
совокупность всех выпуклых фигур на плоскости через
, а
совокупность всех выпуклых фигур на плоскости через 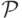 ,
то
тройка функций
,
то
тройка функций 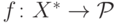 выпуклая
оболочка
последовательности точек,
выпуклая
оболочка
последовательности точек,  ее
периметр и
ее
периметр и 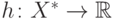 ее площадь в
совокупности задает индуктивную функцию
ее площадь в
совокупности задает индуктивную функцию  ,
, 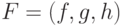 .
.
Функцию перевычисления  для нее более точно мы опишем чуть
позже, а пока
ограничимся следующим предварительным рассуждением. Пусть для некоторой
последовательности точек плоскости выпуклая оболочка, а также ее периметр и
площадь, уже известны. После добавления новой точки
для нее более точно мы опишем чуть
позже, а пока
ограничимся следующим предварительным рассуждением. Пусть для некоторой
последовательности точек плоскости выпуклая оболочка, а также ее периметр и
площадь, уже известны. После добавления новой точки  возможны две
ситуации: либо точка
возможны две
ситуации: либо точка  попадает внутрь оболочки, либо вне ее.
попадает внутрь оболочки, либо вне ее.
В первом случае выпуклая оболочка (а также ее периметр и площадь) не
изменяются. Во втором — изменения происходят, но информации, хранящейся в
функции  (выпуклой оболочки, ее периметра и площади) вместе с
координатами
точки
(выпуклой оболочки, ее периметра и площади) вместе с
координатами
точки  явно достаточно для определения новой выпуклой оболочки и
ее
изменившихся характеристик.
явно достаточно для определения новой выпуклой оболочки и
ее
изменившихся характеристик.
Хорошей моделью для описания изменяющейся оболочки является следующая:
предположим, что во вновь добавляемой точке  расположена
лампочка,
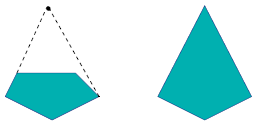
освещающая часть ребер старой оболочки, которые мы так и будем называть — освещенными. Для получения новой оболочки необходимо, как это хорошо
видно из рис. 11.2, удалить
все освещенные ребра, а
концы оставшейся ломаной соединить двумя новыми ребрами с добавляемой
точкой
расположена
лампочка,
освещающая часть ребер старой оболочки, которые мы так и будем называть — освещенными. Для получения новой оболочки необходимо, как это хорошо
видно из рис. 11.2, удалить
все освещенные ребра, а
концы оставшейся ломаной соединить двумя новыми ребрами с добавляемой
точкой  .
.
Если добавляемая точка лежит на продолжении одного из ребер, то оболочка
должна измениться так, как показано на рис.
11.3.
Поэтому ребро, на продолжении которого лежит точка  , мы также
будем считать
освещенным.
, мы также
будем считать
освещенным.
До сих пор рассматривался только общий случай, когда выпуклая оболочка представляла собой многоугольник, однако выпуклая оболочка пустого множества — пустое множество, одной точки — сама эта точка, а двух — отрезок. Эти примеры показывают, что необходимо рассмотреть несколько особых случаев.
Проектирование сверху вниз
Для разработки необходимой иерархии классов в данном случае достаточно воспользоваться давно известным методом — проектированием сверху вниз. Уточненная постановка задачи требует создания класса Convex, необходим еще и класс, содержащий метод main с тестирующей программой. Можно, конечно, добавить этот метод в класс Convex, но мы для этих целей создадим отдельный класс ConvexTest.
Выпуклая оболочка, в любом случае являясь фигурой на плоскости, в процессе добавления точек модифицируется, превращаясь из пустого множества в точку, затем отрезок и, наконец, многоугольник. Подобная ситуация является типичной для использования интерфейса и нескольких различных классов, его реализующих.
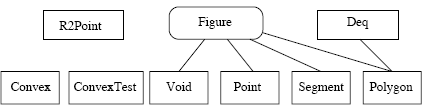
Интерфейс Figure должен содержать общие для всех возможных случаев выпуклой оболочки методы add, perimeter и area, а его реализациями будут являться классы "нульугольник" ( Void ), "одноугольник" ( Point ), "двуугольник" ( Segment ) и многоугольник ( Polygon ). Каждый из этих классов обязан обеспечивать реализацию всех методов интерфейса Figure, при этом метод add должен в качестве аргумента получать добавляемую точку, а возвращать выпуклую оболочку, перевычисленную с ее учетом.
Следовательно, необходим класс, который мы назовем R2Point, представляющий точку на плоскости и обеспечивающий все необходимые действия над объектами этого типа. Его вполне достаточно для реализации классов Void, Point и Segment, ибо в первом случае никакой информации в фигуре хранить вообще не нужно, а в двух последних нужно хранить только один (для "одноугольника") или два (для "двуугольника") экземпляра класса R2Point, представляющие соответственно единственную или две концевых точки этих выпуклых оболочек.
Для класса Polygon, однако, необходимо нечто большее — вершины многоугольника необходимо хранить в каком-то контейнере. Для этих целей особенно хорошо в данном случае подходит дек (это будет понятно уже после того, как программа будет полностью написана), хотя, вообще говоря, можно воспользоваться и другим контейнером.
Итак, класс Deq будет представлять собой непрерывную реализацию дека объектов типа R2Point, а класс Polygon можно просто сделать выведенным (дочерним) для него. При этом класс Polygon оказывается одновременно реализующим ( implements ) интерфейс Figure и расширяющим ( extends ) класс Deq.
Это завершает проектирование иерархии классов, необходимой для решения поставленной задачи. Результат представлен на рис. 11.4.
В заключение данной секции разберемся с тем, как должны быть устроены реализации классов Void, Point и Segment. Для "нульугольника" все очевидно — методы perimeter и area возвращают нулевые значения, а возвращаемым значением метода add должен быть объект типа Point.
Класс "одноугольник" уже должен иметь конструктор с аргументом типа R2Point, сохраняющий эту точку в своей private -компоненте. Периметр и площадь здесь также являются нулевыми, а метод add может возвратить как объект типа Segment, так и неизмененный объект Point. Последнее должно иметь место в случае совпадения вновь добавляемой точки с уже имеющейся. Таким образом, реализация класса Point требует наличия в классе R2Point метода equal, позволяющего сравнивать точки плоскости на равенство. Напомним, что оператор == для объектов ссылочных типов возвращает true только в случае равенства ссылок, а не внутреннего содержания объектов.
Класс "двуугольник" обязан иметь две компоненты типа R2Point, в которые конструктором класса заносятся его концевые точки. Площадь любого "двуугольника" нулевая, а периметром естественно считать удвоенную длину отрезка (сравните "двуугольник" с треугольником). Добавление точки в данном случае может привести к трем различным ситуациям: "двуугольник" может превратиться в треугольник, он может остаться "двуугольником", но изменить одну из своих концевых точек, и, наконец, он может совсем не измениться. Класс R2Point должен обеспечивать методы, которые позволят различать эти ситуации, а итоговый вариант реализации классов Void, Point и Segment приведен в конце лекции.