| подавляющее большиство фукций на пространстве последовательостей? |
Особенности представления чисел в ЭВМ
Как уже отмечалось ранее, множествам целых 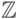 и
действительных
и
действительных  чисел в большинстве языков программирования
соответствуют
их машинные аналоги.
В случае языка Java используемые в программах переменные
величины и константы типов int и double принимают
значения из множеств
чисел в большинстве языков программирования
соответствуют
их машинные аналоги.
В случае языка Java используемые в программах переменные
величины и константы типов int и double принимают
значения из множеств 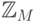 и
и  соответственно.
В этом параграфе мы разберемся с тем, как именно устроены эти
множества, и каковы последствия того, что программы оперируют не с
настоящими числами, а с элементами указанных множеств. Однако сначала —
некоторые напоминания об информации вообще и ее представлении в ЭВМ.
соответственно.
В этом параграфе мы разберемся с тем, как именно устроены эти
множества, и каковы последствия того, что программы оперируют не с
настоящими числами, а с элементами указанных множеств. Однако сначала —
некоторые напоминания об информации вообще и ее представлении в ЭВМ.
Представление информации в компьютере
Любая информация (числовая, текстовая, звуковая, графическая и т.д.) в компьютере представляется (кодируется) в так называемой двоичной форме. Как оперативная, так и внешняя память, где и хранится вся информация, могут рассматриваться, как достаточно длинные последовательности из нулей и единиц. Под внешней памятью подразумеваются такие носители информации, как магнитные и оптические диски, ленты и т.п.
Единицей измерения информации является бит (BInary digiT) — именно такое количество информации содержится в ответе на вопрос: нуль или один? Более крупными единицами измерения информации являются байт, килобайт (Kbyte), мегабайт (Mbyte), гигабайт (Gbyte) и терабайт (Tbyte). Один байт (byte) состоит из восьми бит, а каждая последующая величина больше предыдущей в 1024 раза.
Байта достаточно для хранения 256 различных значений, что позволяет размещать в нем любой из алфавитно-цифровых символов, если только мы можем ограничиться языками с небольшими алфавитами типа русского или английского. Первые 128 символов (занимающие семь младших бит) стандартизированы с помощью кодировки ASCII (American Standart Code for Information Interchange). Хуже обстоит дело с кодировками русского текста (символы русского алфавита расположены во второй половине таблицы из 256 символов) — их несколько, а наиболее распространенные из них сейчас две — Windows-1251 и KOI8-R.
Для кодирования всех возможных символов, используемых народами мира, одного байта мало — необходимо использовать два последовательных (стандарт Unicode). Именно так и поступают при хранении символьных ( char ) значений в языке Java.
Полезно знать, что  .
Учитывая, что в книге
среднего размера около 300000 букв, легко подсчитать, что, даже не используя
никаких средств сжатия информации, на жестком диске современного персонального
компьютера емкостью в 20 гигабайт можно разместить большую библиотеку из
почти 70000 книг.
.
Учитывая, что в книге
среднего размера около 300000 букв, легко подсчитать, что, даже не используя
никаких средств сжатия информации, на жестком диске современного персонального
компьютера емкостью в 20 гигабайт можно разместить большую библиотеку из
почти 70000 книг.
Целые числа
К целочисленным типам в языке Java относятся byte, short, int и long. Для хранения значений этих типов на любом компьютере отводится один, два, четыре и восемь байт соответственно. При этом применяется представление чисел в так называемом двоичном дополнительном коде.
Напомним, что используемая нами обычная система счисления является позиционной с основанием 10.
Это значит, что в ней все натуральные числа
представляются с помощью десяти цифр (от нуля до девяти включительно),
а значение каждой из цифр числа зависит от позиции: самая правая цифра
означает число единиц (  ), вторая — десятков
(
), вторая — десятков
(  ), третья —
сотен (
), третья —
сотен (  ) и так далее.
) и так далее.
В  -ичной системе счисления все точно также, только число 10 в
предыдущем
абзаце нужно всюду заменить на
-ичной системе счисления все точно также, только число 10 в
предыдущем
абзаце нужно всюду заменить на  . Наряду с двоичной
системой, в которой
только две цифры (0 и 1), в информатике часто применяются восьмеричная
с цифрами от нуля до 7 и шестнадцатеричная. В последнем случае в качестве
цифр от десяти до пятнадцати используются буквы от
. Наряду с двоичной
системой, в которой
только две цифры (0 и 1), в информатике часто применяются восьмеричная
с цифрами от нуля до 7 и шестнадцатеричная. В последнем случае в качестве
цифр от десяти до пятнадцати используются буквы от  до
до  соответственно.
соответственно.
При записи положительных целых чисел в системе счисления с основанием  (на компьютере
(на компьютере  ) все их множество оказывается состоящим из
элементов вида
) все их множество оказывается состоящим из
элементов вида

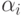 для всех
для всех  из диапазона от
из диапазона от  до нуля —
это цифры
до нуля —
это цифры  -значного числа
-значного числа  в
в  -ичной
системе счисления.
-ичной
системе счисления.Перейдем теперь к вопросу представления отрицательных чисел. Для
определенности
рассмотрим тип byte, в котором любое число занимает ровно восемь бит.
Из записи в двоичной системе счисления равенства  легко
найти,
какой вид должно иметь неизвестное нам пока двоичное представление xxxxxxxx числа
легко
найти,
какой вид должно иметь неизвестное нам пока двоичное представление xxxxxxxx числа  :
:
xxxxxxxx + 00000001 = 00000000
Ясно, что на месте символов xxxxxxxx должно быть расположено число 11111111. Правильным результатом при этом, конечно, следовало бы считать 100000000, а не 00000000, но ведь мы имеем дело с типом byte и, так как результат обязан разместиться в байте, единица "исчезает".
Итак, число  должно кодироваться как 11111111.
Дальнейшее
уже совсем просто: для получения
должно кодироваться как 11111111.
Дальнейшее
уже совсем просто: для получения  нужно
нужно  уменьшить на единицу, что
даст 11111110 ; число
уменьшить на единицу, что
даст 11111110 ; число 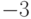 представляется как 11111101
и т.д.
представляется как 11111101
и т.д.
Отрицательные числа всегда имеют в своем двоичном представлении единицу в самом старшем разряде, который поэтому называют знаковым, а абсолютная величина кодируемого числа получается как двоичное дополнение остальных бит (нули нужно заменить на единицы и наоборот), увеличенное на один.
Легко видеть, что при этом самым маленьким отрицательным числом, которое
принадлежит типу byte, является число  (двоичное
представление 10000000 ), а самым большим — число 127 (представление 01111111 ). Все представимые числа (а их 256) в данном случае
могут быть получены как пересечение двух множеств: множества
(двоичное
представление 10000000 ), а самым большим — число 127 (представление 01111111 ). Все представимые числа (а их 256) в данном случае
могут быть получены как пересечение двух множеств: множества 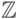 всех целых чисел и отрезка
всех целых чисел и отрезка ![[-128, 127]](/sites/default/files/tex_cache/c151b510eb6ce5e5d9defe6c1b457229.png) . Интересным является
следующее
наблюдение: если число 01111111 увеличить на единицу, то получится 10000000, что означает следующее:
. Интересным является
следующее
наблюдение: если число 01111111 увеличить на единицу, то получится 10000000, что означает следующее: 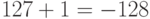 !
!
Итак, множество элементов типа byte можно представлять себе в виде
свернутого в кольцо отрезка ![[-128, 127]](/sites/default/files/tex_cache/c151b510eb6ce5e5d9defe6c1b457229.png) . Принципиально ничего не
меняется
и для типов short, int и long — увеличивается только
длина отрезка, который вырезается из действительной прямой перед сворачиванием
его в кольцо. Минимальные и максимальные представимые значения для каждого из
этих типов в языке Java определены, как значения констант MIN_VALUE и MAX_VALUE в классах java.lang.Short, java.lang.Integer
и java.lang.Long соответственно.
. Принципиально ничего не
меняется
и для типов short, int и long — увеличивается только
длина отрезка, который вырезается из действительной прямой перед сворачиванием
его в кольцо. Минимальные и максимальные представимые значения для каждого из
этих типов в языке Java определены, как значения констант MIN_VALUE и MAX_VALUE в классах java.lang.Short, java.lang.Integer
и java.lang.Long соответственно.
То, что для элементов множества 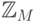 , являющегося
машинным аналогом
, являющегося
машинным аналогом 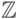 , нарушено фундаментальное свойство целых чисел
, нарушено фундаментальное свойство целых чисел 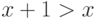 ,
способно привести к различным невероятным на первый взгляд результатам,
однако гораздо более странные вещи происходят при работе с вещественными
числами.
,
способно привести к различным невероятным на первый взгляд результатам,
однако гораздо более странные вещи происходят при работе с вещественными
числами.
